
- •Аналитические методы расчета висячих и вантовых мостов
- •Введение
- •1. Общая характеристика висячих и вантовых мостов
- •1.1. Терминология и классификация
- •1.2. Характеристика типов пролетных строений висячей и вантовой систем и параметры их проектирования
- •1.3. Основные элементы пролетных строений, их конструкция и материалы
- •Основные характеристики канатов
- •1.4. Пилоны висячих и вантовых мостов
- •1.5. Область и перспективы применения висячих и вантовых мостов, их достоинства и недостатки
- •Предельные пролеты мостов различных систем
- •Рекомендуемые диапазоны пролетов
- •2. Вариантное проектирование висячих и вантовых мостов
- •2.1. Основные концепции вариантного проектирования
- •2.2. Эскизное проектирование висячих мостов
- •2.3. Эскизное проектирование вантовых мостов
- •2.4. Эскизное проектирование опор
- •2.5. Определение расхода материалов (веса) элементов висячих и вантовых мостов
- •2.6. Технико-экономическое сравнение вариантов
- •3. Аналитические методы расчета висячих мостов
- •3.1. Теоретические основы расчета висячих мостов
- •3.2. Расчет гибких висячих мостов
- •3.3. Расчет висячих систем с балками жесткости
- •Характеристики линий влияния усилий в элементах
- •Ординаты линий влияния опорного момента для отношений
- •4. Аналитические методы расчета вантовых мостов
- •4.1. Статический расчет методами строительной механики
- •4.2. Приближенные способы расчета
- •4.3. Определение деформаций (прогибов) вантовых систем
- •Контрольные вопросы
- •5. Практический расчет несущих элементов висячих и вантовых мостов
- •5.1. Общие замечания
- •Коэффициенты к нагрузкам
- •5.2. Подбор сечений кабеля, подвесок и вант
- •5.3. Подбор сечений балок жесткости
- •5.4. Подбор сечений пилонов
- •Контрольные вопросы
- •6. Динамический и аэродинамический расчеты висячих и вантовых мостов
- •6.1. Основы динамического расчета
- •6.2. Основы расчета аэродинамической устойчивости
- •Значения для сечений балки жесткости
- •Контрольные вопросы
- •7. Статический расчет висячих и вантовых мостов на эвм
- •7.1. Общие замечания
- •Iбал max {Iбал (1), Iбал (2)}.
- •7.2. Вычислительная программа «Интэл»
- •7.3. Примеры расчета висячих мостов
- •7.4. Примеры расчета балочно-вантовых мостов
- •Заключение
- •Библиографический список
- •Оглавление
- •Аналитические методы расчета висячих и вантовых мостов
- •680021, Г. Хабаровск, ул. Серышева, 47.
- •Аналитические методы расчета висячих и вантовых мостов
3.2. Расчет гибких висячих мостов
К гибким висячим
мостам относятся распорные системы без
балок жесткости или с балкой жесткости
малой высоты
![]() или
или![]()
Степень статической неопределимости висячих систем
![]() (3.8)
(3.8)
где
![]() – степень статической неопределимости
балки жесткости; 1 – то же непрерывного
кабеля при шарнирах наверху пилонов;
– степень статической неопределимости
балки жесткости; 1 – то же непрерывного
кабеля при шарнирах наверху пилонов;![]() – количество нулевых подвесок (приh0
= 0);
– количество нулевых подвесок (приh0
= 0);
![]() – количество жестких закреплений внизу
пилонов;
– количество жестких закреплений внизу
пилонов;![]() – количество шарниров в балке жесткости.
– количество шарниров в балке жесткости.
При расчете гибких висячих систем принимаются следующие условия:
расчет ведется без учета балки жесткости по деформациям кабеля, представляемого в виде гибкой нити;
нагрузки (постоянная и временная) считаются приложенными непосредственно к нити;
уравнение кривой провиса нити от нагрузки
 – квадратная парабола вида
– квадратная парабола вида при
при ;
;угловые и линейные параметры висячей системы определяются следующими соотношениями:
 при
при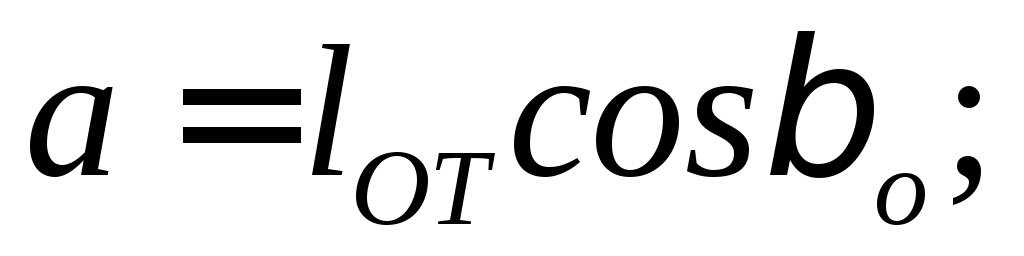
 ;
; ;
; – длина криволинейной части кабеля.
– длина криволинейной части кабеля.
Расчет гибких висячих систем (определение расчетных усилий в отдельныхэлементах) осуществляется в три этапа.
На первом этаперасчетные усилия в элементах системы (рис. 3.4,а) определяются по недеформированной схеме, т. е. без учета удлинения кабеля под действием временной нагрузки и колебаний температуры. При этом распределение временной нагрузкипо всей длине пролета создает наибольшие усилия в гибкой нити и других элементах.

Рис. 3.4. Схемы к расчету гибких висячих мостов: а – схема висячей системы и усилий в элементах; б – расчетная схема кабеля
В соответствии с расчетной схемой (рис. 3.4, б) получены следующие выражения для усилий в элементах:
–
величина распора
![]() – это горизонтальная составляющая
усилия в кабеле, постоянная по всей его
длине кабеля, что обеспечивается
продольно-подвижным опиранием кабеля
на пилонах;
– это горизонтальная составляющая
усилия в кабеле, постоянная по всей его
длине кабеля, что обеспечивается
продольно-подвижным опиранием кабеля
на пилонах;
–
продольное растягивающее усилие в
кабеле, переменное по его длине, имеет
выражение
![]() ;
на вершине пилона
;
на вершине пилона![]()
![]() или
или![]() ;
в середине пролета
;
в середине пролета![]()
–
растягивающие усилия в оттяжках
![]()
–
растягивающие усилия в подвесках,
независимо от их положения по длине
пролета и при равной длине панелей d:
![]()
–
сжимающее усилие в пилоне
![]()
Однако деформации гибкой висячей системы, возникающие от временной нагрузки, а также от удлинения элементов системы под воздействием напряжений и изменения температуры, могут быть значительными, что приводит к существенным ошибкам расчета по недеформированной схеме (в сторону завышения расчетных усилий), а также не обеспечивает нормируемые требования жесткости (по прогибам проезжей части мостов).
В этой связи на втором этаперасчета определяются деформации системы, в частности, дополнительный вертикальный провис кабеля, а следовательно, и балки жесткости.
По схемам деформирования системы (рис. 3.5) от временной нагрузки происходит дополнительное натяжение кабеля и его удлинение, что сопровождается увеличением стрелы провиса на величину z. Этот дополнительный провис кабеля складывается из следующих линейных деформаций элементов:
удлинения оттяжек
 ,
которые сопровождаются смещением
внутрь вершин пилонов или шарнирно-подвижных
опорных частей на величину
,
которые сопровождаются смещением
внутрь вершин пилонов или шарнирно-подвижных
опорных частей на величину пролет кабеля уменьшается на
пролет кабеля уменьшается на
удлинения кабеля в середине пролета

Составив
уравнение деформаций кабеля (с учетом
его криволинейности) на участке между
пилонами (рис. 3.5, а)
в виде
![]() и разрешив его относительноz,
получим
и разрешив его относительноz,
получим
![]()
 ,
(3.9)
,
(3.9)
где
![]() – нормативная временная нагрузка;
– нормативная временная нагрузка;![]() – модуль упругости кабеля;
– модуль упругости кабеля;![]() – площадь сечения кабеля, определенная
по усилию в кабеле
– площадь сечения кабеля, определенная
по усилию в кабеле![]() при расчете на прочность по недеформированной
схеме,
при расчете на прочность по недеформированной
схеме,
![]() при
при
![]() ;а
–
горизонтальное заложение оттяжек;
;а
–
горизонтальное заложение оттяжек;
![]() – длина криволинейной части кабеля;
– длина криволинейной части кабеля;![]() – расчетное сопротивление проволоки
каната [10].
– расчетное сопротивление проволоки
каната [10].
Вертикальные перемещения кабеля от изменения температуры (увеличение или уменьшение) можно приближенно определить по формуле
 (3.10)
(3.10)
где
= 0,000012 град–1
– коэффициент линейного удлинения
кабеля из высокопрочной проволоки
(канатов);
![]() =
40 С
– изменение температуры наружного
воздуха; приведенная длина кабеля вместе
с оттяжками:
=
40 С
– изменение температуры наружного
воздуха; приведенная длина кабеля вместе
с оттяжками:
 ,
,
![]() .
.

Рис. 3.5. Схемы деформирования гибкой висячей системы: а – при загружении временной нагрузкой всего пролета; б – то же половины пролета
Суммарная
деформация кабеля в середине пролета
от временной нагрузки и изменения
температуры определяется с учетом
соответствующих коэффициентов сочетания
этих воздействий
![]() и
и![]() ,
определяемых нормами [10]. Тогда
,
определяемых нормами [10]. Тогда
![]() (3.11)
(3.11)
где
![]() = 0,8,
= 0,8,![]() = 0,7. На практике доказано, что
= 0,7. На практике доказано, что![]() .
.
На третьем этапекорректируются расчетные усилия в элементах висячей системы вследствие ее деформирования, а также проверяются требования действующих норм [10] по жесткости.
Величина распора корректируется с помощью коэффициента
![]() .
.
Тогда, скорректированные значения усилий по деформированной схеме можно записать в следующем виде:
 (3.12)
(3.12)
Оценка достаточной жесткости гибкой
висячей системы производится сравнением
провиса кабеля (прогиб балки жесткости
или проезжей части) в середине пролета
от нормативной временной нагрузки
![]() (при
(при![]() = 1,
= 1,![]() )
с нормируемым значением прогиба
)
с нормируемым значением прогиба
![]() ,
принимаемым в зависимости от назначения
моста по действующим нормам [10].
,
принимаемым в зависимости от назначения
моста по действующим нормам [10].
При выполнении условия
![]() жесткость системы считается обеспеченной.
При условии
жесткость системы считается обеспеченной.
При условии![]() решается вопрос о повышении жесткости
системы за счет применения специальных
конструктивных мер (см. п. 1.2.1) или
увеличения осевой жесткости кабеля
решается вопрос о повышении жесткости
системы за счет применения специальных
конструктивных мер (см. п. 1.2.1) или
увеличения осевой жесткости кабеля![]() .
.
Скорректированная по условию обеспечения необходимой жесткости площадь сечения кабеля определяется по формуле
 (3.13)
(3.13)
