7.2. Интегральная теорема Лапласа

Теорема. Пусть X есть число наступлений события в n независимых опытах, в каждом из которых вероятность появления события равна .Тогда при достаточно большихn вероятность того, что событие появится от дораз, равна

,

где q=1-p, Ф(х) – функция Лапласа.

Эта теорема является следствием из центральной предельной теоремы, хотя и была доказана гораздо раньше неё. В самом деле, число появлений события в n независимых опытах можно представить следующим образом:

,

где – число появлений события в i -м опыте, причём ранее (примеры 4.4 и 4.6) было показано, что и . То естьX является суммой большого числа независимых случайных величин и. Условия центральной предельной теоремы выполнены,X имеет закон распределения, близкий к

Если для этого закона распределения записать вероятность попадания случайной величины в интервал с помощью формулы (5.2), то получим утверждение теоремы Лапласа, которое использовалось ранее (подразд. 2.2).

7.3. Распределение частоты события

Рассмотрим частоту появления события в схеме nнезависимых опытов. Она может быть представлена через индикатор событияI_i, рассмотренный в п. 4.2,в виде

,

т.е. является суммой большого числа независимых одинаково распределенных случайных величин , каждая из которых имеет дисперсию: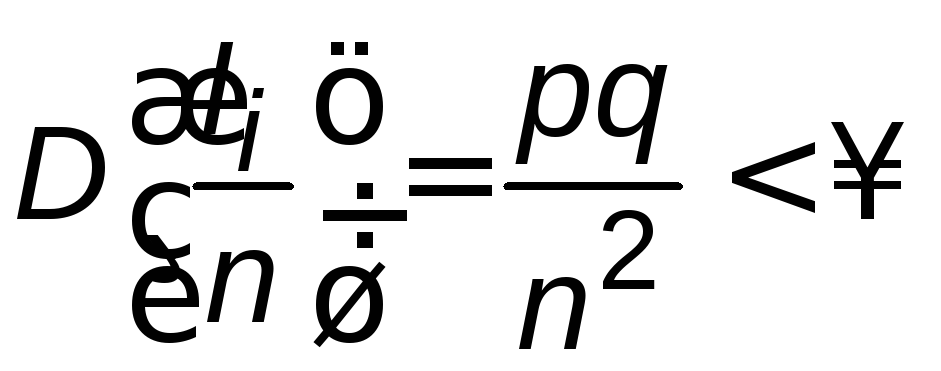(пример 4.6).Согласно центральной предельной теореме частота события имеет закон, близкий к нормальному закону распределения, с параметрами

,

.

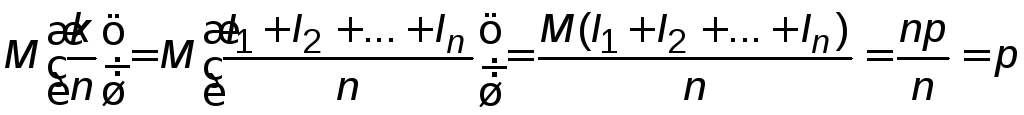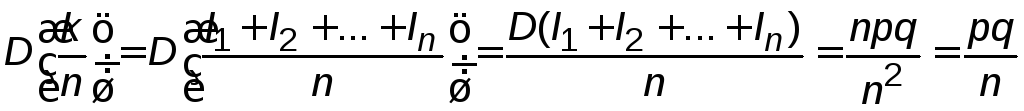Итак, частота события имеет закон распределения, близкий к нормальному 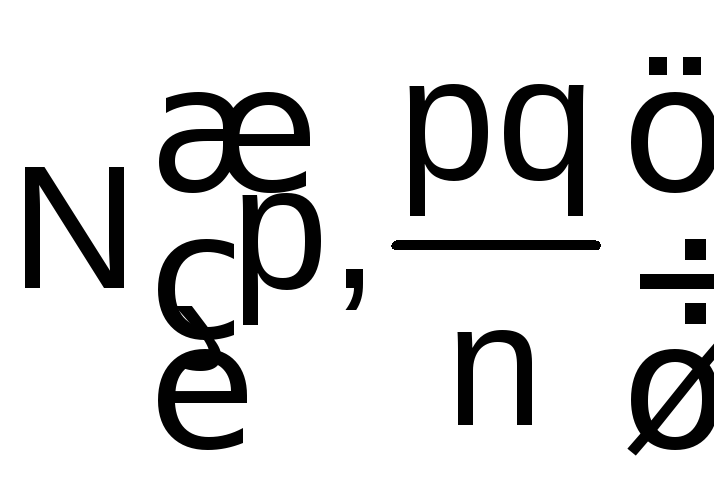. Используя формулу (6.3), можно получить соотношение

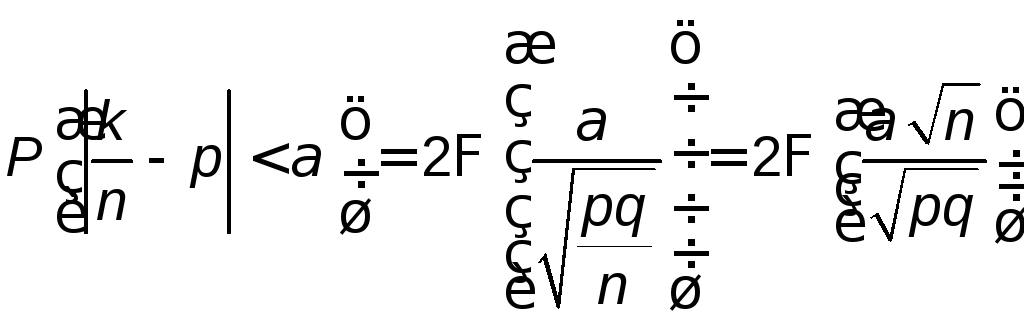(7.1)

для отклонения частоты от вероятностир.

Пример 7.3.

При штамповке 70 % деталей выходит первым сортом, 20 % – вторым и 10 % – третьим. Определить, сколько нужно взять деталей, чтобы с вероятностью, равной 0,997 можно было утверждать, что доля первосортных среди них будет отличаться от вероятности изготовления первосортной детали не более чем на 0,05 в ту или другую сторону? Ответить на тот же вопрос, если процент первосортных деталей неизвестен.

Решение

Изготовление каждой детали можно считать независимым испытанием с вероятностью «успеха» р=0,7. Нужно выбрать число испытаний n, входящих в (7.1):

.

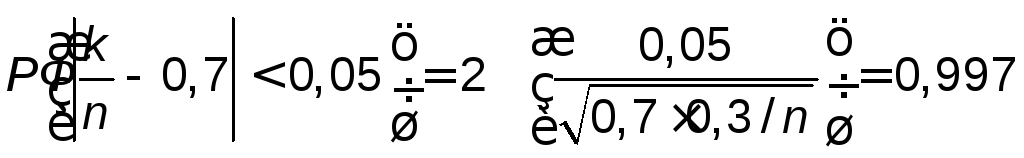По таблице функции Лапласа [4] находим, что 2Ф(2,97)=0,997. Тогда 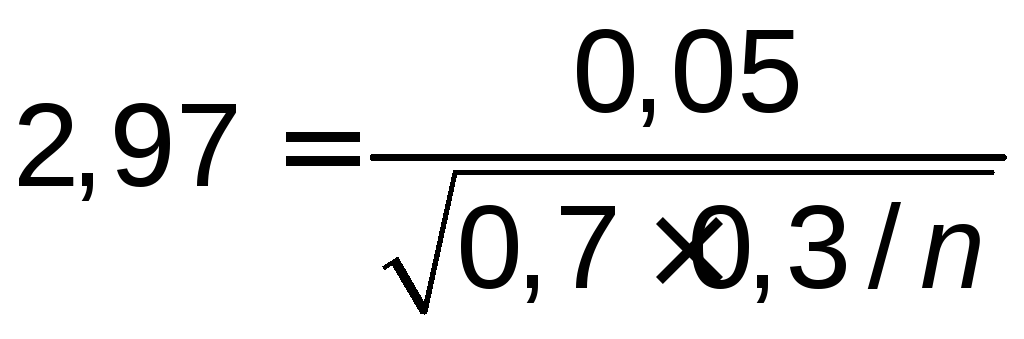, откудаn=741.

Если процент первосортных деталей неизвестен, то 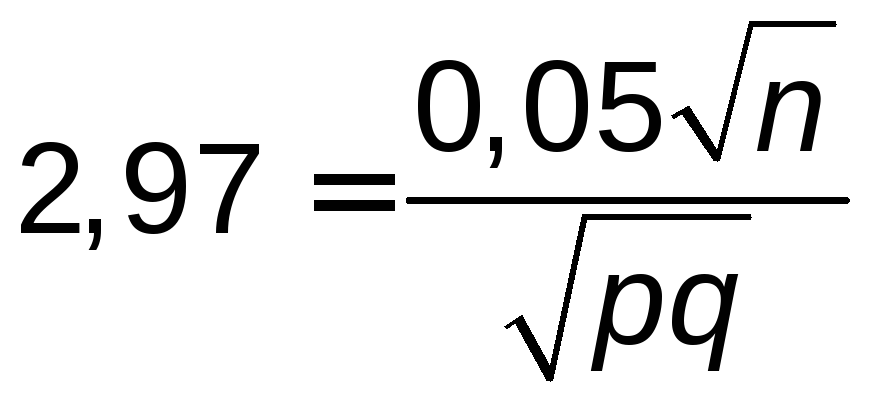, учитывая, чтои заменуp·q на 1/4 придется компенсировать некоторым увеличением n, получаем 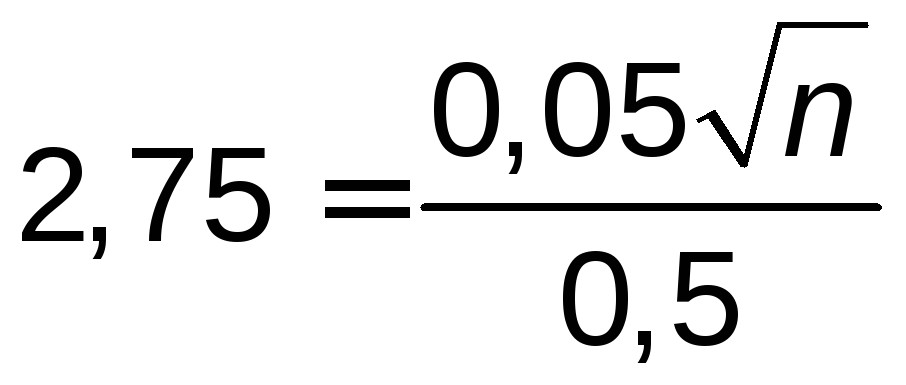илиn=882.

Пример 7.4.

Отдел технического контроля проверяет 4200 радиоламп на стандартность. Вероятность того, что радиолампа стандартная, равна 0,9. Найти такое положительное число α, чтобы с вероятностью 0,516 абсолютная величина отклонения относительной частоты появления стандартной радиолампы от её вероятности не превысила α.

Решение

.

,.

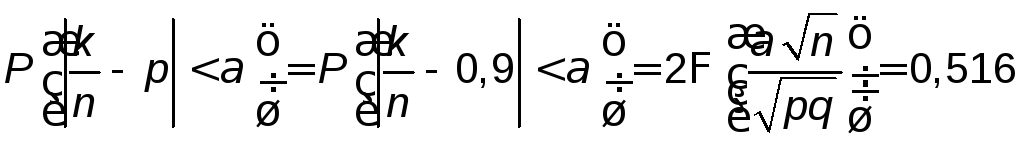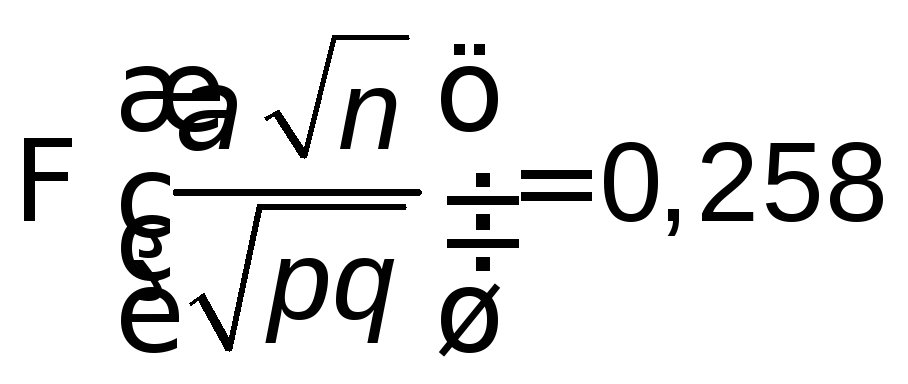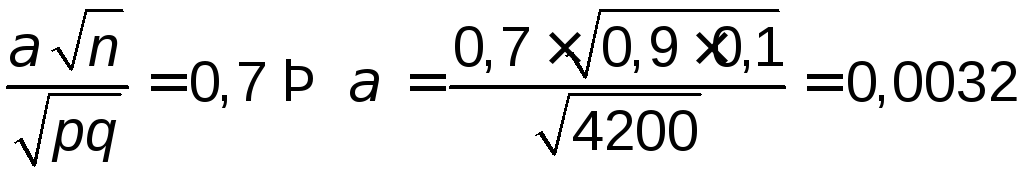7.4. Закон больших чисел

Как уже говорилось, закон больших чисел определяет условия, при которых особенности каждого отдельного случайного явления почти не сказываются на среднем результате совокупности таких явлений. Наиболее яркой иллюстрацией проявления закона больших чисел является постоянство давления газа. Каждая молекула газа, двигаясь хаотично, в случайные моменты времени сталкивается со стенкой сосуда, в который газ заключен. Тем не менее, в виду большого числа молекул, давление газа, как суммарный итог соударений молекул газа со стенками сосуда, практически остаётся постоянным.