
- •Теория вероятностей
- •Введение
- •1. Случайные события. Вероятность событий
- •1.1. Элементы комбинаторики
- •1.1.1 Повторные выборки
- •Число способов выбора двух элементов
- •Число выборок из трех элементов
- •1.1.2. Бесповторные выборки
- •1.2. Основные понятия теории вероятностей
- •1.3. Алгебра событий
- •1.4. Частота события
- •1.5. Статистическое определение вероятности
- •1.6. Классическое определение вероятности
- •1.7. Свойства вероятностей
- •0Р(а)1.
- •1.8. Геометрические вероятности
- •1.9. Теорема умножения вероятностей. Условная вероятность
- •1.10. Теорема сложения вероятностей
- •1.10.1. Вероятность суммы событий
- •1.10.2. Вероятность появления хотя бы одного события
- •1.11. Формула полной вероятности. Формула Байеса
- •1.11.1. Формула полной вероятности
- •1.11.2. Вероятность гипотез. Формула Байеса
- •2. Повторные независимые испытания
- •2.1. Формула Бернулли
- •2.2. Формулы Лапласа
- •2.2.1 Локальная теорема Лапласа
- •2.2.2. Интегральная теорема Лапласа
- •2.3. Формула Пуассона
- •2.4. Простейший поток событий
- •3. Случайные величины
- •3.1. Понятие случайной величины
- •3.2. Законы распределения дискретных случайных величин
- •3.3. Законы распределения непрерывных случайных величин
- •3.3.1. Интегральная функция распределения
- •3.3.2. Показательный закон распределения
- •3.3.3. Дифференциальная функция распределения
- •3.3.4. Равномерное распределение
- •3.3.5. Распределение Коши
- •4. Числовые характеристики случайных величин
- •4.1. Математическое ожидание и его свойства
- •4.1.1. Математическое ожидание
- •4.1.2. Свойства математического ожидания
- •4.2. Дисперсия и среднее квадратическое отклонение
- •4.2.1. Дисперсия случайной величины
- •4.2.2. Свойства дисперсии
- •4.2.3. Среднее квадратическое отклонение
- •4.3. Моменты случайных величин
- •4.4. Примеры нахождения законов распределения
- •5. Нормальный закон распределения
- •5.1. Геометрический смысл параметров m и σ
- •5.2. Вероятностный смысл параметров функции распределения
- •5.3. Вероятность попадания случайной величины в заданный интервал
- •5.4. Вероятность отклонения случайной величины от математического ожидания
- •6. Системы случайных величин
- •6.1. Функция распределения
- •6.2. Плотность распределения
- •6.3. Закон распределения системы двух дискретных случайных величин
- •6.4. Зависимые и независимые случайные величины
- •6.5. Операции над случайными величинами
- •6.6. Числовые характеристики системы двух случайных величин
- •6.6.1. Ковариация двух случайных величин
- •6.6.2 Коэффициент корреляции
- •6.9. Двумерный нормальный закон распределения
- •7. Предельные теоремы теории вероятностей
- •7.1. Центральная предельная теорема
- •7.2. Интегральная теорема Лапласа
- •7.3. Распределение частоты события
- •7.4. Закон больших чисел
- •7.5. Неравенство Чебышева
- •7.6. Теорема Чебышева
- •7.7. Теорема Бернулли
- •7.8. Принцип практической уверенности
- •7.9. Правило трёх сигм
- •Контрольные вопросы
- •Заключение
- •Рекомендуемый Библиографический список
- •Теория вероятностей
- •680021, Г. Хабаровск, ул. Серышева, 47.
2.2. Формулы Лапласа
2.2.1 Локальная теорема Лапласа
Решим следующую задачу (задача Банаха).
Некто носит в кармане две коробки спичек
(по 60 спичек каждая) и всякий раз, когда
нужна спичка, наугад берет коробку и
вынимает спичку. Какова вероятность
того, что когда первая коробка будет
пуста, во второй все еще останется 20
спичек? Выбор коробки можно рассматривать
как независимое испытание, в котором с
вероятностью
![]() выбирается первая коробка. Всего опытов
производитсяn=
60+40=100, и в этих ста опытах первая коробка
должна быть выбрана 60 раз. Вероятность
этого равна:
выбирается первая коробка. Всего опытов
производитсяn=
60+40=100, и в этих ста опытах первая коробка
должна быть выбрана 60 раз. Вероятность
этого равна:
 .
.
Из записи видно, что при больших nпользоваться формулой Бернулли
затруднительно из-за громоздких
вычислений. Существуют специальные
приближенные формулы, которые позволяют
находить вероятности![]() ,
еслиnвелико. Одну из
таких формул дает следующая теорема.
,
еслиnвелико. Одну из
таких формул дает следующая теорема.
Теорема 2.1. (Лапласа локальная).
Если в схеме Бернулли![]() ,
то вероятность того, что событиеAнаступит ровноkраз,
удовлетворяет при большихnсоотношению
,
то вероятность того, что событиеAнаступит ровноkраз,
удовлетворяет при большихnсоотношению
 где
где .
.
Для удобства вводится в рассмотрение
функция
 –
локальная функция Лапласа, с помощью
которой теорему Лапласа можно записать
так:
–
локальная функция Лапласа, с помощью
которой теорему Лапласа можно записать
так:
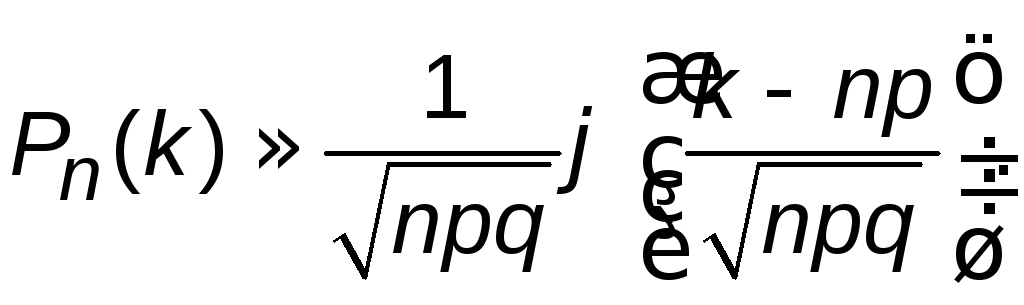
Существуют специальные таблицы функции
![]() [4],
по которым для любого значения:
[4],
по которым для любого значения: можно найти соответствующее значение
функции. Получены эти таблицы путем
разложения функции
можно найти соответствующее значение
функции. Получены эти таблицы путем
разложения функции![]() в ряд.
в ряд.
Геометрически этот результат означает,
что для больших nмногоугольник распределения хорошо
вписывается в график функции, стоящей
в формуле справа (рис. 2.3) и вместо
истинного значения вероятности![]() можно для каждогоkбрать значение функции в точкеk.
можно для каждогоkбрать значение функции в точкеk.

Рис. 2.3. Локальная функция Лапласа
Вернемся теперь к задаче. Используя формулу (2.1) находим:
 ,
,
где значение
![]() определено по таблице [4].
определено по таблице [4].
2.2.2. Интегральная теорема Лапласа
Теорема 2.2 (Лапласа интегральная). Вероятность того, что в схемеnнезависимых испытаний событие наступит отk1доk2раз, приближенно равна
Pn
(k1![]() k2)
k2)![]()
 ,
,
где
![]()
![]()

![]() –
интегральная функция Лапласа, для
которой составлены таблицы. ФункцияФ(х)нечетная:Ф(-х)=-Ф(х) иФ(х
–
интегральная функция Лапласа, для
которой составлены таблицы. ФункцияФ(х)нечетная:Ф(-х)=-Ф(х) иФ(х![]() 4)=0,5.
4)=0,5.
Рассмотрим пока без доказательства еще одно утверждение.
Отклонение относительной частоты
![]() от вероятностиpвnнезависимых испытаниях равно
от вероятностиpвnнезависимых испытаниях равно
(
 .
.
Замечание.Обоснование этих фактов будет рассмотрено далее в разделе 7 (подразд. 7.2, 7.3). Теоремы Лапласа иногда называют теоремами Муавра–Лапласа.
Пример 2.3.
Вероятность появления события в каждом из 900 независимых испытаний равна 0.5. 1) найти вероятность того, что событие произойдет от 400 до 500 раз, 2) найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
Решение
1) Р900(400<k<500)= =
=

2)

 =
=![]()
2.3. Формула Пуассона
Если зафиксировать число опытов n, а вероятность появления события в одном опытеризменять, то многоугольник распределения будет иметь различный вид в зависимости от величиныр(рис.2.4). При значенияхp, близких к 1/2, многоугольник почти симметричен и хорошо вписывается в симметричный график функции Лапласа. Поэтому приближенная формула Лапласа дает хорошую точность.
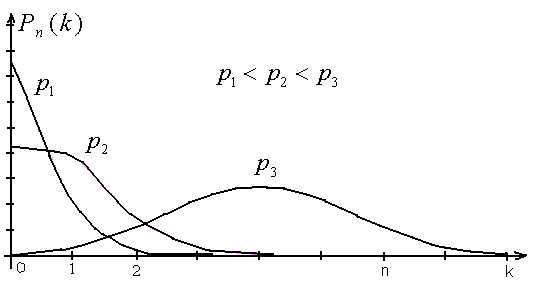
Рис. 2.4.
Для малых р(на практике меньших![]() )
приближение плохое из-за несимметричности
многоугольника распределения. Поэтому
возникает задача найти приближенную
формулу для вычисления вероятностей
)
приближение плохое из-за несимметричности
многоугольника распределения. Поэтому
возникает задача найти приближенную
формулу для вычисления вероятностей![]() в случае большихnи
малых р. Ответ на этот вопрос дает
формула Пуассона.
в случае большихnи
малых р. Ответ на этот вопрос дает
формула Пуассона.
Итак, рассмотрим схему независимых испытаний, в которой nвелико (чем больше, тем лучше), армало (чем меньше, тем лучше). Обозначимnр=λ. Тогда по формуле Бернулли имеем
 .
.
Последнее равенство верно в силу того,
что
 (второй замечательный предел). При
получении формулы наивероятнейшего
числа появления событияk0было рассмотрено отношение вероятностей.
Из него следует, что
(второй замечательный предел). При
получении формулы наивероятнейшего
числа появления событияk0было рассмотрено отношение вероятностей.
Из него следует, что

Таким образом, при kмного меньшихnимеем рекуррентное соотношение
![]() .
.
Для k=0 учтем полученный
ранее результат:![]() ,
тогда
,
тогда
![]()


………………

Итак, если в схеме независимых испытаний nвелико, ар мало, то имеет местоформула Пуассона
Рn(к)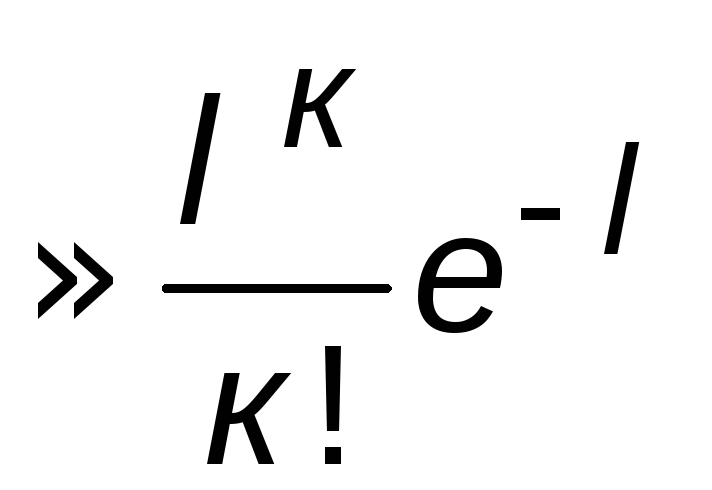 ,
где λ=nр.
,
где λ=nр.
Закон Пуассона еще называют законом редких явлений.
Пример 2.4.
Вероятность выпуска бракованной детали равна 0,02. Детали упаковываются в коробки по 100 штук. Какова вероятность того, что а) в коробке нет бракованных деталей, б) в коробке больше двух бракованных деталей?
Решение
a) Так какnвелико, армало, имеем
![]() ;
Р100(0)
;
Р100(0) ;
;
б)Р100(k>2)=1-Р![]() 1-
1-
Таким образом, в схеме независимых испытаний для вычисления вероятности Рn(k)следует пользоваться формулой Бернулли, еслиnневелико, а еслиnвелико, то в зависимости от величиныриспользуется одна из приближенных формул Лапласа или формула Пуассона.
