5. Нахождение неизвестных параметров в случае задания эмпирической формулы в виде многочлена или показательной функции.

Пусть в качестве аппроксимирующей функции выбран многочлен степени :

Тогда сумма квадратов отклонений примет вид:

,

а неизвестные параметры будут определяться системой уравнений:

Если приближающая функция выбрана в виде показательной функции, то выражение можно светсти к линейному, логарифмируя левую и правую части равенства:

или .

После введения обозначений: ,;, функциязаписывается как линейная по аргументу:

Сумма отклонений определяется формулой:

,

а коэффициенты инаходятся из решения системы:

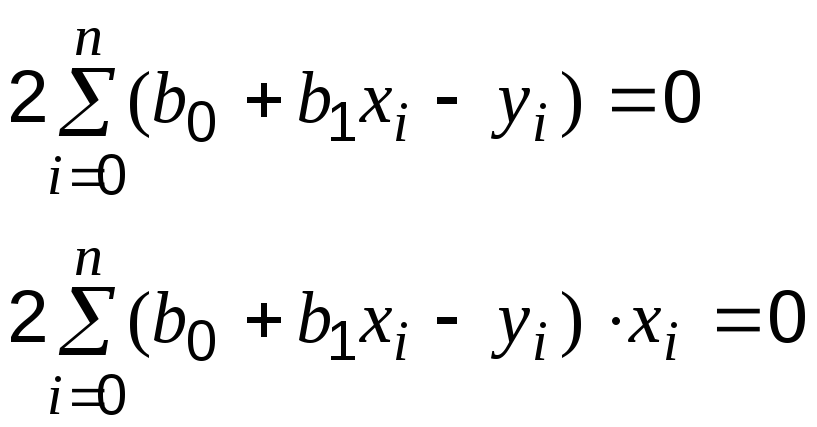
после чего осуществляется обратный переход к параметрам и.

Аналогично можно поступать и в тех случаях, когда в качестве аппроксимирующей функции выбраны, например, гипербола или логарифмическая функция.

6. Примеры построения различных видов аппроксимирующих функций.

Пусть функция задана таблицей 3.1. Требуется построить методом наименьших квадратов функцию, приближающую табличную наилучшим образом. Для удобства обозначений изменим нумерацию исходных данных и будем считать, что ;;;;;;;;. Сделаем предположение относительно характера аппроксимирующуей функции, рассмотрев расположение точек, заданных таблицей, на графике (рис. 1.).

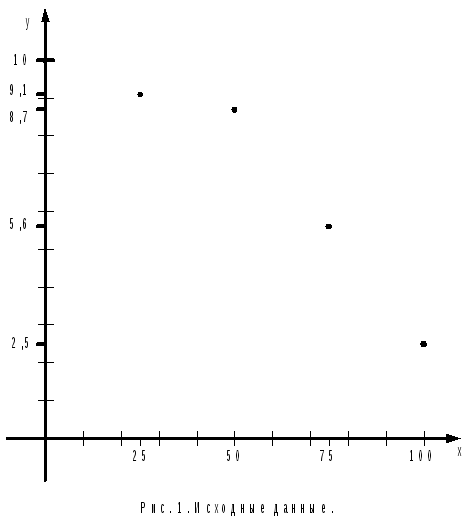
По характеру расположения точек на графике можно выдвинуть предположение о линейной квадратичной или показательной зависимости величин. Рассмотрим все три предположения.

Случай 1. Будем искать приближающую функциюв виде линейной функции.

Сумма мер отклонений , где;- число измерений. Найдём неизвестные коэффициенты из системы:

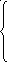
После преобразования система принимает вид:

…(1)

Составим вспомогательную таблицу

Таблица 6.1.

	0	10	0	0
	25	9,1	625	227,5
	50	8,7	2500	435
	75	5,6	5625	420
	100	2,5	10000	250
	250	35,9	18750	1332,5

Подставив данные из таблицы 6.1 в систему (1), получим:

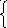
откуда , а уравнение линейной функции

.

Случай 2. Аппроксимирующая функция – квадратичная.

Сумма мер отклонений . Неизвестные коэффициенты будут найдены из системы:

,

преобразовав которую, получим:

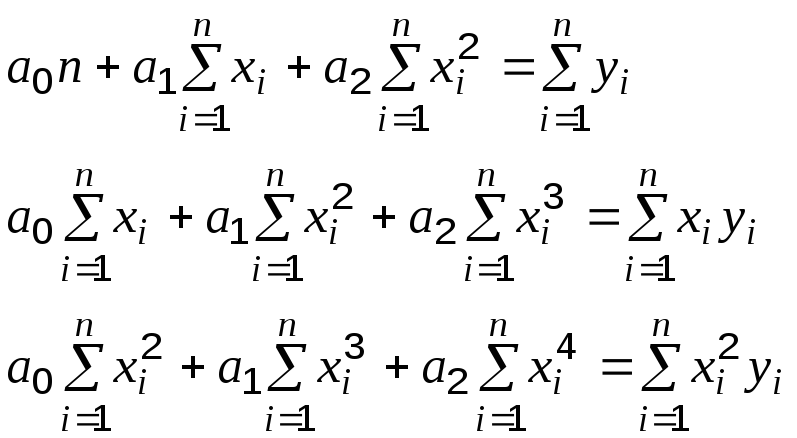
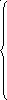…(2)

Составим вспомогательную таблицу.

Таблица 6.2

	0	0	0	0	10	0	0
	25	625	15625	390625	9,1	227,5	5687,5
	50	2500	125000	6250000	8,7	435	21750
	75	5625	421875	31640625	5,6	420	31500
	100	10000	1000000	100000000	2,5	250	25000
	250	18750	1562500	138281250	35,9	1332,5	83937,5

Подставим данные из таблицы 6.2 в систему (2):

и, решив её, получим значения параметров:

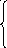
Уравнение квадратичной зависимости:

Случай 3. Найдем приближающую функцию в виде показательного выражения. После логарифмирования показательной функции

и введения обозначений ;;, функциязаписывается как линейная.

Построим таблицу соответствия известных значений:

Таблица 6.3

	0	10	2,30	0	0
	25	9,1	2,20	625	55
	50	8,7	2,16	2500	108
	75	5,6	1,72	5625	129
	100	2,5	0,92	10000	92
	250	35,9	9,3	18750	384

Запишем систему:

Подставим данные из таблицы 6.3 в систему (3):

и получим в результате:

Возвращаясь к показательной функции, запишем:

; ;.

Значения линейной функции: ;

Квадратичной функции:

Показательной функции:

и их отклонения от табличных значений функции в заданных точках сведём в таблицу 6.4

Таблица 6.4

	0	25	50	75	100
	10	9,1	8,7	5,6	2,5
	0,88	-0,07	-1,52	-0,27	0,98
	-0,13	0,44	-0,51	0,24	-0,03
	2,28	-0,22	-2,28	-0,95	0,86

На основании таблицы 6.4 вычисляется сумма квадратов отклонений аппроксимации для каждого из трёх рассмотренных видов приближения:

Следовательно, для заданной табличной функции наиболее целесообразна квадратичная аппроксимация.

По полученным результатам строятся графики.