
- •Змістовий модуль 8.
- •8.1.2. Властивості невизначеного інтеграла
- •8.1.3. Таблиця основних невизначених інтегралів
- •8.2. Основні методи інтегрування
- •8.2.1. Метод безпосереднього інтегрування
- •8.2.3. Метод інтегрування частинами
- •8.3. Інтегрування раціональних функцій
- •8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру)
- •Дробово-раціональна функція
- •8.3.2. Інтегрування найпростіших раціональних дробів
- •8.3.3. Інтегрування раціональних дробів
- •8.4. Інтегрування тригонометричних функцій
- •8.4.1. Універсальна тригонометрична підстановка
- •8.4.2. Інтеграли виду
- •8.4.3. Використання тригонометричних перетворень
- •8.5. Інтегрування ірраціональних функцій
- •8.5.1. Квадратичні ірраціональності
- •8.5.2. Дробово-лінійна підстановка
- •8.5.3. Тригонометрична підстановка
- •8.5.4. Інтеграли виду
- •8.5.5. Інтегрування диференціального бінома
- •8.6. Інтеграли, що «беруться» і «не беруться»
8.5.2. Дробово-лінійна підстановка
Інтеграли
виду
 ,
де
,
де -
дійсні числа,
-
дійсні числа, – натуральні числа, зводяться до
інтегралів від раціональної функції
шляхом підстановки
– натуральні числа, зводяться до
інтегралів від раціональної функції
шляхом підстановки ,
де
,
де – найменше спільне кратне знаменників
дробів
– найменше спільне кратне знаменників
дробів .
.
Дійсно,
з підстановки
 виходить, що
виходить, що і
і ,
тобто
,
тобто і
і виражаються через раціональні функції
від
виражаються через раціональні функції
від .
При цьому і кожний степінь дробу
.
При цьому і кожний степінь дробу виражається через раціональну функцію
від
виражається через раціональну функцію
від .
.
Приклад
4. Знайти
інтеграл
 .
.
Найменше
спільне кратне знаменників дробів
 і
і є6.
Тому
вважаємо
є6.
Тому
вважаємо
 ,
, ,
, ,
,
 .
Отже
.
Отже


 .
.
Приклад 5.Вказати підстановку для знаходження інтегралів:
Для
 підстановка
підстановка
 ,
для
,
для підстановка
підстановка
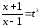 .
.
8.5.3. Тригонометрична підстановка
Інтеграли
типу
 зводяться
до інтегралів від функцій, раціонально
залежних від тригонометричних функцій,
за допомогою наступних тригонометричних
підстановок:
зводяться
до інтегралів від функцій, раціонально
залежних від тригонометричних функцій,
за допомогою наступних тригонометричних
підстановок:
 для першого інтеграла;
для першого інтеграла; для другого інтеграла;
для другого інтеграла; для третього інтеграла.
для третього інтеграла.
Приклад
6.
Знайти інтеграл
 .
.
Покладемо
 ,
, ,
,
 .
Тоді
.
Тоді



 .
.
8.5.4. Інтеграли виду
Тут
підінтегральна функція є раціональною
функцією відносно
 і
і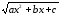 .
Виділивши під радикалом повний квадрат
і зробивши підстановку
.
Виділивши під радикалом повний квадрат
і зробивши підстановку ,
інтеграли вказаного типу приводяться
до інтегралів вже розглянутого типу,
тобто до інтегралів типу
,
інтеграли вказаного типу приводяться
до інтегралів вже розглянутого типу,
тобто до інтегралів типу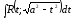 ,
,
 .
Ці інтеграли можна обчислити за допомогою
відповідних тригонометричних підстановок.
.
Ці інтеграли можна обчислити за допомогою
відповідних тригонометричних підстановок.
Приклад
7.
Знайти інтеграл
 .
.
Оскільки
 ,
то
,
то
 ,
, ,
, .
Тому
.
Тому .
Покладемо
.
Покладемо ,
, .
Тоді
.
Тоді




 .
.
Зауваження:
Інтеграл типу
 доцільно знаходити за допомогою
підстановки
доцільно знаходити за допомогою
підстановки .
.
8.5.5. Інтегрування диференціального бінома
Інтеграли
типу
 (названі інтегралами від диференціального
бінома), де
(названі інтегралами від диференціального
бінома), де –
дійсні числа;
–
дійсні числа; –
раціональні числа, беруться, як показав
Чебишoв
П.А., лише у разі, коли хоча б одне з чисел
–
раціональні числа, беруться, як показав
Чебишoв
П.А., лише у разі, коли хоча б одне з чисел
 ,
, або
або є цілим.
є цілим.
Раціоналізація інтеграла в цих випадках здійснюється наступними підстановками:
1)
якщо
 - ціле число, то підстановка
- ціле число, то підстановка ,
де
,
де –
найменше спільне кратне знаменників
дробів
–
найменше спільне кратне знаменників
дробів
 і
і ;
;
2)
якщо
 - ціле число, то підстановка
- ціле число, то підстановка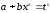 ,
де
,
де - знаменник
дробу
- знаменник
дробу
 .
.
3)
якщо
 -
ціле число, то підстановка
-
ціле число, то підстановка
 ,
де
,
де - знаменник дробу
- знаменник дробу .
.
У
всій решті випадків інтеграли типу
 не виражаються через відомі елементарні
функції, тобто не «беруться».
не виражаються через відомі елементарні
функції, тобто не «беруться».
Приклад
8.
Знайти інтеграл
 .Оскільки
.Оскільки
 то
то ,
,
 ,
,

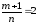 .
Тому робимо
підстановку
.
Тому робимо
підстановку
 .
Таким чином,
.
Таким чином,

 .
.
8.6. Інтеграли, що «беруться» і «не беруться»
Як
вже наголошувалося вище, операція
інтегрування функцій значно складніша
за операцію диференціювання функцій.
Не завжди вибраний шлях інтеграції є
найкращим, більш коротким, простим.
Інтегрування часто може бути виконане
не єдиним способом. Багато що залежить
від рекомендованого знання багатьох
штучних прийомів інтегрування, від
кмітливості, від натренованості.
Наприклад,
 можна знайти, не використовуючи
рекомендовану підстановку
можна знайти, не використовуючи
рекомендовану підстановку ,
а застосувавши штучний прийом:
,
а застосувавши штучний прийом:

 .
.
Навряд
чи варто обчислювати інтеграл
 ,
розкладаючи
підінтегральну функцію на найпростіші
дроби:
,
розкладаючи
підінтегральну функцію на найпростіші
дроби:
 .
.
Помітивши,
що чисельник
 є
похідною знаменника
є
похідною знаменника ,
легко отримати:
,
легко отримати:

 .
.
На практиці при обчисленні невизначених інтегралів використовують різні довідники, що містять таблиці інтегралів, які часто зустрічаються. Зокрема, «Таблиці невизначених інтегралів» М.Л.Смолянського.
Вивчені методи інтеграції дозволяють у багатьох випадках обчислити невизначений інтеграл, тобто знайти первісну функцію для підінтегральної функції.
Як
відомо, всяка неперервна функція має
первісну. У тому випадку, коли первісна
деякій елементарній функції
 є
також елементарною функцією, говорять,
що
є
також елементарною функцією, говорять,
що «береться», тобто інтеграл виражається
через елементарні функції (або інтеграл
обчислюється). Якщо ж інтеграл не
виражається через елементарні функції,
то говорять, що інтеграл не «береться»
(або «його знайти не можна»).
«береться», тобто інтеграл виражається
через елементарні функції (або інтеграл
обчислюється). Якщо ж інтеграл не
виражається через елементарні функції,
то говорять, що інтеграл не «береться»
(або «його знайти не можна»).
Так,
наприклад, не можна узяти інтеграл
 ,
оскільки не існує елементарної функції,
похідна від якої б була рівна
,
оскільки не існує елементарної функції,
похідна від якої б була рівна .
Наведемо ще приклади інтегралів, що не
«беруться», які мають велике значення
в додатках:
.
Наведемо ще приклади інтегралів, що не
«беруться», які мають велике значення
в додатках:
 -
інтеграл Пуассона (теорія імогідності)
-
інтеграл Пуассона (теорія імогідності)
 -
інтегральний логарифм (теорія чисел)
-
інтегральний логарифм (теорія чисел)
 -
інтеграли Френеля (фізика)
-
інтеграли Френеля (фізика)
 -
інтегральні синус і косинус
-
інтегральні синус і косинус
 -
інтегральна показова функція.
-
інтегральна показова функція.
Первісні
від функції ,
, ,
, і інших добре вивчені, для них складені
докладні таблиці значень для різних
значень аргументу
і інших добре вивчені, для них складені
докладні таблиці значень для різних
значень аргументу .
.
