
- •Змістовий модуль 8.
- •8.1.2. Властивості невизначеного інтеграла
- •8.1.3. Таблиця основних невизначених інтегралів
- •8.2. Основні методи інтегрування
- •8.2.1. Метод безпосереднього інтегрування
- •8.2.3. Метод інтегрування частинами
- •8.3. Інтегрування раціональних функцій
- •8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру)
- •Дробово-раціональна функція
- •8.3.2. Інтегрування найпростіших раціональних дробів
- •8.3.3. Інтегрування раціональних дробів
- •8.4. Інтегрування тригонометричних функцій
- •8.4.1. Універсальна тригонометрична підстановка
- •8.4.2. Інтеграли виду
- •8.4.3. Використання тригонометричних перетворень
- •8.5. Інтегрування ірраціональних функцій
- •8.5.1. Квадратичні ірраціональності
- •8.5.2. Дробово-лінійна підстановка
- •8.5.3. Тригонометрична підстановка
- •8.5.4. Інтеграли виду
- •8.5.5. Інтегрування диференціального бінома
- •8.6. Інтеграли, що «беруться» і «не беруться»
8.3.3. Інтегрування раціональних дробів
Розглянутий в пунктах 1-3 матеріал дозволяє сформулювати загальне правило інтеграції раціональних дробів.
Якщо дріб неправильний, то подати його у вигляді суми многочлена і правильного дробу (див. пункт 2);
Розклавши знаменник правильного раціонального дробу на множники, подати його у вигляді суми найпростіших раціональних дробів;
Проінтегрувати многочлен і отриману суму найпростіших дробів.
Приклад
7.
Знайти інтеграл
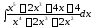 .
.
Під знаком інтеграла неправильний дріб; виділимо його цілу частину шляхом ділення чисельника на знаменник:
_ x5 +2x3 +4x+4|x4 +2x3 +2x2
х5+2x4 +2x3 |x–2
_–2x4 +4x+4
–2x4–4x3–4x2
4x3+4x2+4x+4 (остача).
Отримаємо:

Розкладемо правильний раціональний дріб на найпростіші дроби:

 ,
,

 ,
тобто
,
тобто

 .
.
Звідси слідує, що

Знаходимо:
 .
Отже
.
Отже
 ,
і
,
і
 .
.
Інтегруємо отриману рівність:

 .
.
Позначимо
 ,
тоді
,
тоді і
і .
Таким чином
.
Таким чином

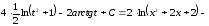
 .
.
Отже
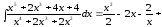
 .
.
Відзначимо, що будь-яка раціональна функція інтегрується в елементарних функціях.
8.4. Інтегрування тригонометричних функцій
8.4.1. Універсальна тригонометрична підстановка
Розглянемо деякі
випадки знаходження інтеграла від
тригонометричних функцій. Функцію із
змінними
 і
і ,
над якими виконуються раціональні дії
(додавання, віднімання, множення і
ділення) прийнято позначати
,
над якими виконуються раціональні дії
(додавання, віднімання, множення і
ділення) прийнято позначати ,
де
,
де – знак раціональної функції.
– знак раціональної функції.
Обчислення
невизначених інтегралів типу
 зводиться до обчислення інтегралів від
раціональної функції підстановкою
зводиться до обчислення інтегралів від
раціональної функції підстановкою ,
яка називаєтьсяуніверсальною.
,
яка називаєтьсяуніверсальною.
Дійсно
 .
.
Тому
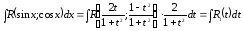
де
 - раціональна функція від
- раціональна функція від
 .
Звичайно, цей спосіб досить громіздкий,
зате він завжди приводить до результату.
.
Звичайно, цей спосіб досить громіздкий,
зате він завжди приводить до результату.
На практиці застосовують і інші, більш прості підстановки, залежно від властивостей (і вигляду) підінтегральної функції. Зокрема, зручні наступні правила:
1)
якщо функція
 непарна відносно
непарна відносно ,
тобто
,
тобто ,
то підстановку
,
то підстановку раціоналізує
інтеграл;
раціоналізує
інтеграл;
2)
якщо функція
 непарна відносно
непарна відносно ,
тобто
,
тобто ,
то виконується підстановка
,
то виконується підстановка ;
;
3)
якщо функція
 парна відносно
парна відносно і
і ,
тобто
,
тобто ,
то інтеграл раціоналізується підстановкою
,
то інтеграл раціоналізується підстановкою .
Така ж підстановка застосовується, якщо
інтеграл має вигляд
.
Така ж підстановка застосовується, якщо
інтеграл має вигляд .
.
Приклад
1.
Знайти інтеграл

Зробимо
універсальну підстановку
 .
Тоді,
.
Тоді, .
Отже
.
Отже

 .
.
Приклад
2.
Знайти інтеграл
 .
.
Оскільки

 ,
то вважаємо
,
то вважаємо
 .
Звідси
.
Звідси
 ,
,
 і
і .
.
Тому
 .
.
8.4.2. Інтеграли виду
Для знаходження таких інтегралів використовуються наступні прийоми:
1)
підстановка
 ,
якщо
,
якщо – ціле додатне непарне число;
– ціле додатне непарне число;
2)
підстановка
 ,
якщо
,
якщо – ціле додатне непарне число;
– ціле додатне непарне число;
3)
формули пониження порядку:


 ,
якщо
,
якщо
 і
і - цілі невід’ємні парні числа;
- цілі невід’ємні парні числа;
4)
підстановка
 ,
якщо
,
якщо –
є парне від’ємне ціле число.
–
є парне від’ємне ціле число.
Приклад
3.
Знайти інтеграл
 .
.
Застосуємо
підстановку
 .
Тоді
.
Тоді ,
, і
і

 .
.
Приклад
4.
Знайти інтеграл
 .
.


 .
.
Приклад
5.
Знайти інтеграл
 .
.
Тут
 .
Позначимо
.
Позначимо .
Тоді
.
Тоді ,
, і
і

 .
.
8.4.3. Використання тригонометричних перетворень
Інтеграли
типу
 ,
, ,
, обчислюються за допомогою відомих
тригонометричних формул:
обчислюються за допомогою відомих
тригонометричних формул:
 ,
,
 ,
,
 .
.
Приклад
6.
Знайти інтеграл
 .
.

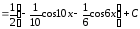 .
.
8.5. Інтегрування ірраціональних функцій
8.5.1. Квадратичні ірраціональності
Розглянемо деякі типи інтегралів, що містять ірраціональні функції.
Інтеграли
типу ,
,
 називають
невизначеними
інтегралами від квадратичних
ірраціональностей.
Їх можна знайти таким чином: під радикалом
виділити повний квадрат
називають
невизначеними
інтегралами від квадратичних
ірраціональностей.
Їх можна знайти таким чином: під радикалом
виділити повний квадрат


і
зробити підстановку
 .
При цьому перші два інтеграли приводяться
до табличних, а третій – до суми двох
табличних інтегралів.
.
При цьому перші два інтеграли приводяться
до табличних, а третій – до суми двох
табличних інтегралів.
Приклад
1.
Знайти інтеграли
 .
.
Оскільки
 ,
то
,
то .
.
Зробимо
підстановку ,
, ,
, .
Тоді
.
Тоді

 .
.
Приклад
2.
Знайти інтеграл
 .
.
Оскільки
 ,
то підстановка має вигляд
,
то підстановка має вигляд ,
, ,
, .
Тоді
.
Тоді



 .
.
Інтеграли
типу ,
де
,
де - многочлен степеня
- многочлен степеня можна обчислювати, користуючись формулою
можна обчислювати, користуючись формулою

 (5.1)
(5.1)
де
 -
многочлен степеня
-
многочлен степеня з невизначеними коефіцієнтами,
з невизначеними коефіцієнтами, – також невизначений коефіцієнт.
– також невизначений коефіцієнт.
Всі невизначені коефіцієнти знаходяться з тотожності, отриманої диференціюванням обох частин рівності (5.1):

 ,
після
чого необхідно прирівняти коефіцієнти
при однакових степенях невідомої
,
після
чого необхідно прирівняти коефіцієнти
при однакових степенях невідомої
 .
.
Приклад
3.
Знайти інтеграл

По формулі (5.1) маємо:

 .
.
Диференціюючи цю рівність, отримаємо:

 ,
тобто
,
тобто
 ,
,
 .
Порівнюємо
коефіцієнти при однакових
степенях
.
Порівнюємо
коефіцієнти при однакових
степенях
 :
:
 ,
при
,
при

 при
при

 при
при

Звідси

 .
Отже
.
Отже

 .
.
