Дробово-раціональна функція

Дробово-раціональною функцією (або раціональним дробом) називається функція, рівна відношенню двох многочленів, тобто , де- многочлен степеня , а - многочлен степеня.

Раціональний дріб називається правильним, якщо степінь чисельника менше степеня знаменника, тобто ; в протилежному випадку(якщо ) раціональний дріб називається неправильним.

Всякий неправильний раціональний дріб можна, шляхом ділення чисельника на знаменник, подати у вигляді суми многочленаі правильного раціонального дробу, тобто.

Наприклад,– неправильний раціональний дріб. Розділимо чисельник на знаменник в стовпчик:

_ х⁴ –5х +9|х–2

х⁴–2х³ |х³ +2x² +4x+3

_ 2х³ –5х + 9

2х³–4х²

_4х² – 5х + 9

4х² – 8х

_ 3х + 9

3х – 6

15.

Отримаємо часткуі залишок. Отже,

.

Правильні раціональні дроби вигляду

(I).;

(II).;

(III).(корені знаменника комплексні, тобто);

(IV).(, корені знаменника комплексні) , де - дійсні числа, називаютьсянайпростішими раціональними дробами I, II, III і IV типів.

Теорема 8.3.8. Всякий правильний раціональний дріб, знаменник якого розкладений на множники

, можна подати (і притому єдиним чином) у вигляді наступної суми найпростіших дробів:

, (3.6)

де – деякі дійсні коефіцієнти.

Пояснимо формулювання теореми на наступних прикладах:

1) ;

2) ;

3) .

Для знаходження невизначених коефіцієнтів в рівності (3.6) можна застосувати метод порівняння коефіцієнтів.

Суть методу така:

1. В правій частині рівності (3.6) зведемо до спільного знаменника; в результаті отримаємо тотожність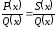, де – многочлен з невизначеними коефіцієнтами.

2. Оскільки в отриманій тотожності знаменники рівні, то тотожно рівні і чисельники, тобто

. (3.7)

3. Прирівнюючи коефіцієнти при однакових степенях (по теоремі 31.5 про тотожність многочленів) в обох частинах тотожності (3.7), отримаємо систему лінійних рівнянь, з якої і визначимо шукані коефіцієнти

Приклад 3. Подати дріб у вигляді суми найпростіших дробів.

 Згідно теореми 31.8 маємо:

, тобто

.

Звідси слідує

, тобто

.

Прирівнюючи коефіцієнти при , отримаємо

Розв’язуючи систему, знаходимо, що . Отже,

. 

Для знаходження невизначених коефіцієнтів застосовують також метод окремих значень аргументу: після отримання тотожності (3.7) аргументу надають конкретні значення стільки раз, скільки невизначених коефіцієнтів (звичайно вважають зазначення дійсних коренів многочлена).

Приклад 4. Подати дріб у вигляді суми найпростіших дробів.

 Маємо: . Звідси слідує

Покладемо , тоді, тобто; покладемо, тоді , тобто; покладемо, тоді, тобто. Отже

.

8.3.2. Інтегрування найпростіших раціональних дробів

Знайдемо інтеграли від найпростіших раціональних дробів.

1. (формула (2) таблиці інтегралів);

2. (формула (1));

3. Розглянемо інтеграл .

Виділивши в знаменнику повний квадрат, отримаємо:

,

причому . Зробимо підстановку. Тоді,. Покладемо. Отже, використовуючи формули (2) і (15) таблиці інтегралів, отримуємо:

,

тобто, повертаючись до змінної

.

Приклад 5. Знайти .

 . Зробимо підстановку . Тоді,і

. 

4. Обчислення інтеграла вигляду .

Даний інтеграл підстановкою зводиться до суми двох інтегралів:,.

Перший інтеграл легко обчислюється:

.

Обчислимо другий інтеграл:

. (3.8)

До останнього інтеграла застосуємо інтегрування частинами. Покладемо

, тоді

Підставляючи знайдений інтеграл в рівність (3.8), отримаємо

, тобто

.

Отримана формула дає можливість знайти інтеграл для будь-якого натурального числа .

Приклад 6. Знайти інтеграл .

 Тут до . Оскільки , то

,

. 