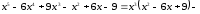- •Змістовий модуль 8.
- •8.1.2. Властивості невизначеного інтеграла
- •8.1.3. Таблиця основних невизначених інтегралів
- •8.2. Основні методи інтегрування
- •8.2.1. Метод безпосереднього інтегрування
- •8.2.3. Метод інтегрування частинами
- •8.3. Інтегрування раціональних функцій
- •8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру)
- •Дробово-раціональна функція
- •8.3.2. Інтегрування найпростіших раціональних дробів
- •8.3.3. Інтегрування раціональних дробів
- •8.4. Інтегрування тригонометричних функцій
- •8.4.1. Універсальна тригонометрична підстановка
- •8.4.2. Інтеграли виду
- •8.4.3. Використання тригонометричних перетворень
- •8.5. Інтегрування ірраціональних функцій
- •8.5.1. Квадратичні ірраціональності
- •8.5.2. Дробово-лінійна підстановка
- •8.5.3. Тригонометрична підстановка
- •8.5.4. Інтеграли виду
- •8.5.5. Інтегрування диференціального бінома
- •8.6. Інтеграли, що «беруться» і «не беруться»
8.2.3. Метод інтегрування частинами
Нехай
 і
і - функція, що має неперервні похідні.
Тоді
- функція, що має неперервні похідні.
Тоді .
Проінтегрувавши цю рівність, отримаємо
.
Проінтегрувавши цю рівність, отримаємо
 або
або

Отримана формула
називається формулою
інтегрування частинами.
Вона дає можливість звести обчислення
інтеграла
 до обчислення інтеграла
до обчислення інтеграла ,
який може виявитися істотно простішим
за початковий.
,
який може виявитися істотно простішим
за початковий.
Інтегрування
частинами полягає в тому, що підінтегральний
вираз заданого інтеграла представляється
яким-небудь чином у вигляді добутку
двох співмножників
 і
і
 (це,
як правило, можна здійснити декількома
способами); потім, після знаходження
(це,
як правило, можна здійснити декількома
способами); потім, після знаходження
 і
і
 використовується формула інтегрування
частинами. Іноді цю формулу потрібно
використовувати кілька разів.
використовується формула інтегрування
частинами. Іноді цю формулу потрібно
використовувати кілька разів.
Вкажемо деякі типи інтегралів, які зручно обчислювати методом інтегрування частинами.
Інтеграл вигляду
 ,
де
,
де -
многочлен,
-
многочлен,
 – число. Зручно покласти
– число. Зручно покласти
 ,
а за
,
а за позначити
решту співмножників.
позначити
решту співмножників.Інтеграли вигляду

 .
Зручно покласти
.
Зручно покласти ,
а за
,
а за позначити
решту співмножників.
позначити
решту співмножників.Інтеграли вигляду
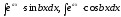 ,
де
,
де і
і – числа. За
– числа. За можна
прийняти функцію
можна
прийняти функцію
 .
.
Приклад
6.
Знайти
 .
.
Нехай
 (можна
покласти
(можна
покласти
 ).
Отже, по формулі інтегрування частинами:
).
Отже, по формулі інтегрування частинами:

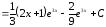 .
.
Приклад
7.
Знайти
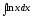 .
.
Нехай
 .
Тому
.
Тому
 .
.
Приклад
8.
Знайти
 .
.
Нехай
 .
Тому
.
Тому
 .
(2.2)
.
(2.2)
Для
обчислення інтеграла
 знову застосуємо метод інтегрування
частинами:
знову застосуємо метод інтегрування
частинами: .
Значить
.
Значить
 .
(2.3)
.
(2.3)
Тому
(див. (2.2)) .
.
Приклад
9.
Знайти
 .
.
Нехай
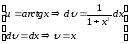 .
Тому
.
Тому

 .
.
8.3. Інтегрування раціональних функцій
8.3.1. Поняття про раціональні функції Многочлен (деякі відомості довідкового характеру)
Функція вигляду
 (3.1)
(3.1)
де
 —
натуральне число,
—
натуральне число,
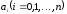 — постійні коефіцієнти, називаєтьсямногочленом
(або
цілою
раціональною функцією).
— постійні коефіцієнти, називаєтьсямногочленом
(або
цілою
раціональною функцією).
Число
 називається
степенем
многочлена.
називається
степенем
многочлена.
Коренем
многочлена
(3.1) називається таке значення
 (взагалі кажучи, комплексне) змінної
(взагалі кажучи, комплексне) змінної ,
при якому многочлен перетворюється в
нуль, тобто
,
при якому многочлен перетворюється в
нуль, тобто .
.
Теоремa
8.3.1.
Якщо
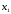 є коренем многочлена
є коренем многочлена ,
то многочлен ділиться без остачі на
,
то многочлен ділиться без остачі на тобто
тобто
 (3.2)
(3.2)
де
 — многочлен степеня
— многочлен степеня .
.
Виникає питання: чи всякий многочлен має корінь? Позитивну відповідь на це питання дає наступне твердження.
Теорема
8.3.2.
(основна теорема алгебри).
Всякий
многочлен
 -го
степеня
-го
степеня
 має
принаймні один корінь, дійсний або
комплексний.
має
принаймні один корінь, дійсний або
комплексний.
Доведення цієї теореми ми не приводимо. Користуючись основною теоремою алгебри, доведемо теорему про розкладання многочлена на лінійні множники.
Теорема
8.3.3.
Всякий
многочлен
 можна подати у вигляді
можна подати у вигляді
 (3.3)
(3.3)
де
 —
корені многочлена,
—
корені многочлена,
 — коефіцієнт многочлена при
— коефіцієнт многочлена при .
.
Розглянемо
многочлен (3.1). По теоремі 8.3.2
він має корінь. Позначимо його через
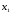 .
Тоді має місце співвідношення (3.2). А
оскільки
.
Тоді має місце співвідношення (3.2). А
оскільки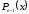 — також многочлен, то він має корінь.
Позначимо його через
— також многочлен, то він має корінь.
Позначимо його через .
.
Тоді
 ,
де
,
де — многочлен
— многочлен -го
степеня. Отже,
-го
степеня. Отже, .
.
Продовжуючи цей процес, отримаємо у результаті:
 .
.
Множники
 в рівності (3.3) називаютьсялінійними
множниками.
в рівності (3.3) називаютьсялінійними
множниками.
Приклад
1.
Розкласти
многочлен
 на множники.
на множники.
Многочлен
 перетворюється в нуль при
перетворюється в нуль при .
Отже,
.
Отже, .
.
Приклад
2.
Представити вираз
 у вигляді добутку лінійних множників.
у вигляді добутку лінійних множників.
Легко
перевірити, що

Якщо
в розкладанні многочлена (3.3) який-небудь
корінь зустрівся
 раз, то він називаєтьсякоренем
кратності
раз, то він називаєтьсякоренем
кратності .
У випадку
.
У випадку
 (тобто корінь зустрівся один раз) корінь
називаєтьсяпростим.
(тобто корінь зустрівся один раз) корінь
називаєтьсяпростим.
Розкладання многочлена (3.3) можна записати у вигляді
 ,
(3.4)
,
(3.4)
якщо
корінь
 має кратність
має кратність ,
корінь
,
корінь –
кратність
–
кратність
 і так далі.
і так далі.
При
цьому
 ,
а
,
а – число різних коренів.
– число різних коренів.
Наприклад, розкладання
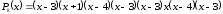
можна записати так:
 .
.
Користуючись теоремою 31.3, можна довести наступні твердження.
Теорема
8.3.4.
Якщо
многочлен
 тотожно рівний нулю, то всі його
коефіцієнти рівні нулю.
тотожно рівний нулю, то всі його
коефіцієнти рівні нулю.
Теорема 8.3.5. Якщо два многочлени тотожно рівні один одному, то коефіцієнти одного многочлена рівні відповідним коефіцієнтам іншого.
Наприклад,
якщо,
 ,
то
,
то
 .
.
Теорема
8.3.6.
Якщо
многочлен
 з дійсними коефіцієнтами має комплексний
корінь
з дійсними коефіцієнтами має комплексний
корінь ,
то він має і зв'язаний корінь
,
то він має і зв'язаний корінь .
.
В розкладанні многочлена (3.3) комплексні корені входять спряженими парами. Перемноживши лінійні множники
 ,
,
отримаємо
тричлен другого степеня з дійсними
коефіцієнтами
 .
Насправді,
.
Насправді,
 де
де
 .
.
Таким чином, добуток лінійних множників, відповідних зв'язаним кореням, можна замінити квадратним тричленом з дійсними коефіцієнтами.
З урахуванням вищевикладеного справедливий наступний факт.
Теорема
8.3.7.
Всякий
многочлен з дійсними коефіцієнтами
розкладається на лінійні і квадратні
множники з дійсними коефіцієнтами,
тобто многочлен
 можна подати у вигляді
можна подати у вигляді

 .
(3.5)
.
(3.5)
При
цьому
 всі
квадратні тричлени не мають речовинних
коренів.
всі
квадратні тричлени не мають речовинних
коренів.
Приклади розкладань (3.5):
1)

2)

3)