8.1.3. Таблиця основних невизначених інтегралів

Користуючись тим, що інтеграція – це дія, зворотна диференціюванню, можна отримати таблицю основних інтегралів шляхом обігу відповідних формул диференціального числення (таблиця диференціалів) і використовування властивостей невизначеного інтеграла.

Наприклад, оскільки

,

то

.

Вивід ряду формул таблиці буде даний при розгляді основних методів інтегрування.

Інтеграли, що приводяться нижче в таблиці називаються табличними. Їх слід знати напам'ять. В інтегральному численні немає простих і універсальних правил пошуку первісних від елементарних функцій, як в диференціальному численні. Методи знаходження первісних (тобто інтеграції функції) зводяться до вказівки прийомів, що приводять даний (шуканий) інтеграл до табличного. Отже, необхідно знати табличні інтеграли і уміти їх розпізнавати.

Відзначимо, що в таблиці основних інтегралів змінна інтеграції може позначати як незалежну змінну, так і функцію від незалежної змінної (згідно властивості інваріантності формули інтеграції).

В справедливості приведених нижче формул можна переконатися, узявши диференціал правої частини, який буде рівний підінтегральному виразу в лівій частині формули.

Доведемо, наприклад, справедливість формули 2. Функція визначена і неперервна для всіх значень, відмінних від нуля.

Якщо , то, тоді .

Тому при.

Якщо 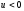, то. Але. Значитьпри.

Отже, формула 2 вірна.

Аналогічно, перевіримо формулу 15:

.

Таблиця основних інтегралів

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. ;

17. ;

18. 

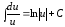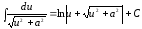8.2. Основні методи інтегрування

8.2.1. Метод безпосереднього інтегрування

Метод інтегрування, при якому даний інтеграл шляхом тотожних перетворень підінтегральної функції (або виразу) і застосування властивостей невизначеного інтеграла зводиться до одного або декількох табличних інтегралів, називається безпосереднім інтегруванням.

При зведенні даного інтеграла до табличного часто використовуються наступні перетворення диференціала (операція «приведення під знак диференціала»):

, – число

, – число

,

,

,

,

.

Взагалі, , ця формула дуже часто використовується при обчисленні інтегралів.

Приклади:

1) (формула 2 таблиці інтегралів);

2) (формула 1);

3)

(формули 10 і 1);

4)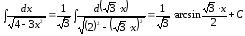 (формула 13);

5)

(формули 1 і 6);

6)

;

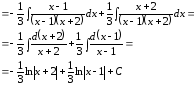7) (виведення формули 7);

8)

(виведення формули 11);

9)

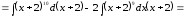
(формула 1);

10) (формула 1);

11) 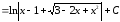(формула 14);

12)

(формули 1,9,3);

13)

.

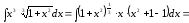
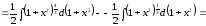
Як бачимо, обчислення інтегралів іноді вимагає деякої винахідливості, так би мовити, «індивідуального підходу до кожної підінтегральної функції».

Відповідні навички отримуються в результаті значного числа вправ.

8.2.2. Метод інтегрування підстановкою (заміна змінної)

Інтегрування методом підстановки полягає у введенні нової змінної інтегрування (тобто підстановкою). При цьому заданий інтеграл приводиться до нового інтеграла, який є табличним або таким, що зводиться до нього (у разі «вдалої підстановки»). Загальних методів підбору підстановок не існує. Уміння правильно визначити підстановку отримується практикою.

Нехай потрібно обчислити інтеграл 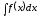. Зробимо підстановку, де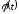– функція, що має неперервну похідну.

Тоді і на підставі властивості інваріантності формули інтеграції невизначеного інтеграла отримуємоформулу інтегрування підстановкою

(2.1)

Формула (2.1) також називається формулою заміни змінних в невизначеному інтегралі. Після знаходження інтеграла правої частини цієї рівності слід перейти від нової змінної інтеграції назад до змінної .

Іноді доцільно підбирати підстановку у вигляді , тоді, де. Іншими словами, формулу (2.1) можна застосовувати справа наліво.

Приклад 1. Знайти .

 Покладемо , тоді. Отже . 

Приклад 2. Знайти .

 Нехай , тоді,. Тому

.

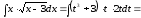
Приклад 3. Отримати формулу .

Позначимо 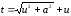(підстановка Ейлера). Тоді , тобто.

Звідси

.

Отже

. 

Приклад 4. Знайти .

 Нехай . Тоді,. Маємо:

. 

Приклад 5. Знайти .

 Позначимо 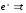. Тоді,. Отже

.

Тут використовується формула 16 таблиці основних інтегралів. 