
- •Міністерство освіти і науки, молоді та спорту україни
- •Розділ 1
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •1.2. Знакозмінні ряди
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Відповіді.
- •2.2. Розвинення функцій у степеневі ряди
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Завдання для самостійної роботи
- •4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Відповіді
- •4.3. Ряди Фур’є 2l- періодичних функцій
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •Відповіді
- •4.4. Ряди Фур’є для функцій, заданих на проміжку
- •Зразки розв’язання задач
- •Завдання для самостійної роботи
- •Відповіді
- •Література
- •З м і с т
- •49600, М. Дніпропетровськ-5, пр. Гагаріна, 4
Завдання для самостійної роботи
Знайти перші три ненульові члени розвинення у степеневий ряд розв’язку задачі Коші
1.
![]() ,
,![]() .
.
2.
![]() ,
,![]() ,
,![]() .
.
Знайти розвинення у степеневий ряд розв’язку задачі Коші
3.
![]() ,
,![]() ,
,![]()
4.
![]() ,
,![]() ,
,![]()
Відповіді
1.
![]() .
.
2.
![]() .
.
3.
![]() ;
;
![]() .
.
4.
![]() ;
;
![]() .
.
Розділ 4
РЯДИ ФУР’Є
4.1. Основні формули
Основні формули, за якими будуються розвинення в ряд Фур’є функцій та обчислюються коефіцієнти цих розвинень, наведені у вигляді таблиці.
|
Період
Парність |
|
|
|
Загального вигляду
|
|
|
|
Парна
|
|
|
|
Непарна
|
|
|
У процесі обчислення коефіцієнтів Фур’є часто застосовуються деякі відомі математичні формули та факти. Наведемо їх.
Формули перетворення добутків тригонометричних формул в суму
![]()
![]()
![]()
Важливі властивості тригонометричних функцій
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Деякі формули інтегрування
![]()
![]()
![]()
4.2.Розвинення в ряди Фур’є 2π-періодичних функцій
Розглянемо
деяку 2π-періодичну
функцію
![]() ,
неперервну, або таку, що на відрізку
,
неперервну, або таку, що на відрізку![]() має скінчене число точок розриву першого
роду.
має скінчене число точок розриву першого
роду.
Функціональний
ряд виду
![]() ,
коефіцієнти
якого обчислюються за формулами
,
коефіцієнти
якого обчислюються за формулами
![]() ,
,
![]() ,
,
![]() ,
,
називається
рядом Фур’є функції
![]() .
Цей ряд збігається для будь-якого
значення
.
Цей ряд збігається для будь-якого
значення![]() ,
у всіх точках неперервності функції
сума ряду
,
у всіх точках неперервності функції
сума ряду![]() ,
а в точках розриву сума ряду дорівнює
півсумі лівосторонньої та правосторонньої
границь функції
,
а в точках розриву сума ряду дорівнює
півсумі лівосторонньої та правосторонньої
границь функції![]() :
:
![]() .
.
Якщо
2π-періодична
функція
f(x)
є
парною (![]() ),
то вона розкладається в ряд Фур’є тільки
за косинусами:
),
то вона розкладається в ряд Фур’є тільки
за косинусами:
![]() ,
,
де
![]()
![]() .
.
Непарна 2π- періодична функція f(x) розкладається в ряд Фур’є тільки за синусами:
![]() ,
,
де
![]() .
.
Зразки розв’язування задач
Побудувати ряд Фур’є для заданої функції
1.
![]() ,
,
![]() ;
;![]() .
.
![]() ,
,
тобто це функція загального виду, отже, ряд Фур’є цієї функції має вигляд
![]() .
.
Обчислимо коефіцієнти цього ряду.
![]()
![]()
![]()
![]()
![]() ;
;
![]()
![]()


![]()
![]()
![]()
![]() ;
;
![]()
![]()


![]()
![]()
![]()
![]()
![]() .
.
Таким чином, ряд Фур’є має вигляд
![]() .
.
2.
![]() ,
,![]() ;
;
![]()
![]() ,
,
тобто функція є парною, а її ряд Фур’є має вигляд
![]() .
.
Обчислимо коефіцієнти ряду.
![]()

![]() ;
;
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]() .
.
Отже,
![]() .
.
3.
Функція
![]() задана графічно.
задана графічно.
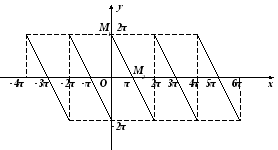
Рис.4.1
Графік даної функції симетричний відносно початку координат, тому функція непарна, періодична с періодом 2π.
Ряд Фур’є має вигляд
![]() де
де
![]() .
.
Задамо
функцію
![]() аналітично.
Графік функції – пряма, що сполучає
точки
аналітично.
Графік функції – пряма, що сполучає
точки
![]() та
та![]() .Запишемо рівняння прямої
.Запишемо рівняння прямої![]() :
:
![]()
![]()
![]() .
.
Тоді
![]()



 .
.
Таким чином, ряд Фур’є функції, зображеної на рис.1, виглядає так:
![]() .
.
Завдання для самостійної роботи
Знайти ряд Фур’є для функцій
1.
 .
.
2.
![]() .
.
3.
На проміжку
![]() функцію задано графічно;
функцію задано графічно;![]() .
.
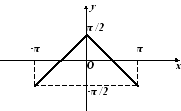
Рис. 4.2
Відповіді
1.
![]() .
.
2.
![]() .
.
3.
![]()
4.3. Ряди Фур’є 2l- періодичних функцій
Якщо f(x) є функцією періоду 2l, її розвинення в ряд Фур’є має вигляд
![]() ,
,
де коефіцієнти обчислюються за формулами
![]() ,
,
![]() ,
,
![]() .
.
Для парних функцій формули мають вигляд
![]() ,
,
![]() ,
,
![]() ,
,
а для непарних –
![]() ,
,
![]() .
.
Зразки розв’язання задач
1.
![]() ,
, ![]() ;
;
![]()
Функція
є періодичною з періодом
![]() ,
отже,
,
отже,![]() .
.
![]() – функція загального вигляду,
– функція загального вигляду,
отже,
![]() .
.
Обчислимо коефіцієнти ряду.
![]()
![]() ;
;
![]()


![]()

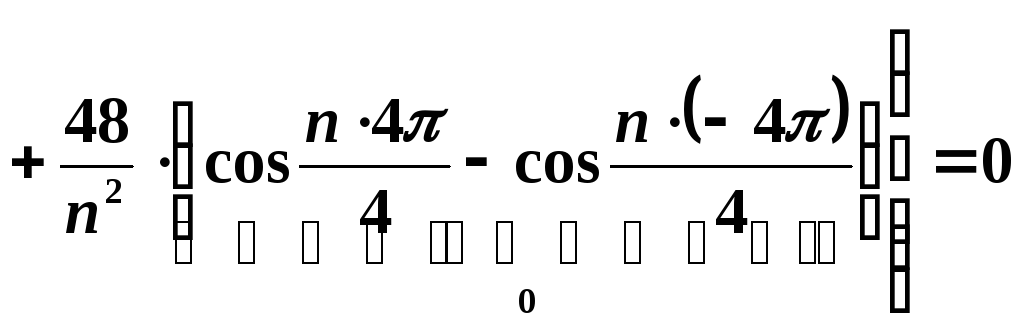 ;
;
![]()


![]()
![]()

![]()
![]()
![]() .
.
Остаточно
![]() .
.
2.
 ;
;
![]()
Функція
є періодичною з періодом
![]() ,
отже,
,
отже,![]() .
Очевидно, що функція є ні парною, ні
непарною, отже,
.
Очевидно, що функція є ні парною, ні
непарною, отже,
![]() .
.
Обчислимо коефіцієнти ряду.
 ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
![]()
 ,
,
![]()

![]()
![]()


![]() ,
,
![]()
![]()
![]() ,
,
![]() ;
;
![]()
 ,
,
![]()

![]()
![]()


![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() .
.
Таким чином, ряд має вигляд
![]() .
.
3.
![]() ,
, ![]() ;
;
![]() .
.
Функція
має період
![]() ,
отже,
,
отже,
![]() .
.
![]() –функція
непарна, тобто її ряд Фур’є має вигляд
–функція
непарна, тобто її ряд Фур’є має вигляд
![]() .
.
Обчислимо коефіцієнти ряду.


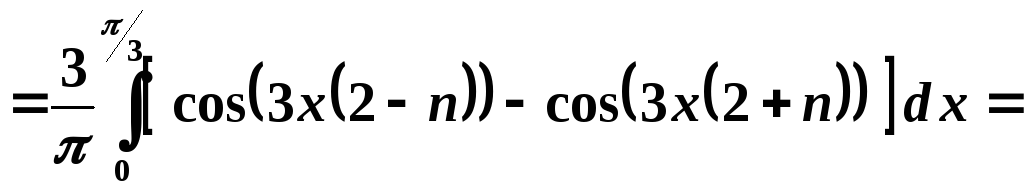

 .
.
Отриманий
результат справджується для ![]() ,
оскільки застосування відомої формули
з таблиці інтегралів можливо лише, якщо
,
оскільки застосування відомої формули
з таблиці інтегралів можливо лише, якщо
![]() .
.
Окремо
обчислимо коефіцієнт
![]() :
:

![]() .
.
Таким
чином, ![]() ,
або
,
або
![]() .
.
Отриманий
результат є очікуваним, оскільки функція
![]() співпадає з однією з функцій системи,
за якою будується розвинення.
співпадає з однією з функцій системи,
за якою будується розвинення.
4.
На
проміжку
![]() періодичну з періодом
періодичну з періодом![]() функцію
y=f(x)
задано
графічно.
функцію
y=f(x)
задано
графічно.

Рис.4.3
Період
функції 2l=8,
отже, півперіод l=4.
Графік є симетричним відносно осі
![]() ,
тому функція парна та розкладається в
ряд Фур’є за косинусами:
,
тому функція парна та розкладається в
ряд Фур’є за косинусами:
![]() .
.
Задамо
функцію аналітично.
Запишемо
рівняння прямої, яка проходить через
точки![]() та
та![]() .
.
Користуючись
рівнянням
![]() ,
маємо
,
маємо
![]()
![]()
![]() .
.
Таким
чином,
![]() для
для
![]() .
.
Якщо
![]() , то
, то
![]() ;
при
;
при
![]()
![]() .
.
Остаточно
 .
.
Обчислимо коефіцієнти Фур’є:


![]() ;
;
![]()
![]()



![]()

![]() .
.
![]() .
.
Зауваження.
Також цілком коректною є задача побудови
ряду Фур’є для функції, яку задано лише
на скінченому проміжку
![]() .
Треба лише зауважити, що застосовувати
отримане розвинення можна виключно для
значень аргументу із зазначеного
проміжку.
.
Треба лише зауважити, що застосовувати
отримане розвинення можна виключно для
значень аргументу із зазначеного
проміжку.
