
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
9.7.2. Обчислення площ плоских фігур
Як
вже було встановлено (див. «геометричне
значення визначеного інтеграла»), площа
криволінійної трапеції, розташованої
«вище» за вісь абсцис ( ),
дорівнює відповідному визначеному
інтегралу:
),
дорівнює відповідному визначеному
інтегралу:
 .
(9.7.1)
.
(9.7.1)
Формула
(9.7.1) отримана шляхом застосування першої
схеми—методу сум. Обґрунтуємо формулу
(9.7.1), використовуючи другу схему. Нехай
криволінійна трапеція обмежена лініями
 (див. рис..174).
(див. рис..174).

(рис.174)
Для знаходження площі S цієї трапеції виконаємо наступні операції:
Візьмемо довільне
 і вважатимемо, що
і вважатимемо, що .
.Дамо аргументу
 приріст
приріст
 .
Функція
.
Функція
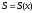 отримає
приріст
отримає
приріст
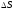 ,
який є площею «елементарної криволінійної
трапеції» (на малунку вона виділена).
,
який є площею «елементарної криволінійної
трапеції» (на малунку вона виділена).
Диференціал
площі
 це головна частина приросту
це головна частина приросту
 при
при
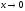 ,
і, очевидно, він дорівнює площі прямокутника
з основою
,
і, очевидно, він дорівнює площі прямокутника
з основою
 і висотою
і висотою
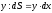 .
.
Інтегруючи одержану рівність в межах від
 до
до
 ,
отримаємо
,
отримаємо
 .
.
Відзначимо,
що якщо криволінійна трапеція розташована
«нижче» осі
 ,
то її площа може бути знайдена по формулі
,
то її площа може бути знайдена по формулі
 .
(9.7.2)
.
(9.7.2)
Формули (9.7.1) і (9.7.2) можна об'єднати в одну:
 .
.

(рис.175)
Площа
фігури, обмеженої кривими
 і
і
 ,
прямими
,
прямими
 і
і
 (при умові
(при умові
 )
(див. рис. 175), можна знайти по формулі
)
(див. рис. 175), можна знайти по формулі
 .
(*)
.
(*)

(рис.176)
Якщо
плоска фігура має «складну» форму (див.
рис. 176), то прямими, паралельними осі
 ,
її слід розбити на частини так, щоб можна
б було застосувати відомі формули.
,
її слід розбити на частини так, щоб можна
б було застосувати відомі формули.
Якщо
криволінійна трапеція обмежена прямими
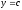 і
і
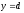 ,
віссю
,
віссю
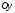 і неперервною кривою
і неперервною кривою
 (див. рис.177), то її площа знаходиться по
формулі
(див. рис.177), то її площа знаходиться по
формулі
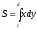 .
.

(рис.177)
І, нарешті, якщо криволінійна трапеція обмежена кривою заданою параметрично
 ,
,
прямими
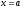 ,
,
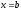 і віссю
і віссю
 ,
то площа її знаходиться по формулі
,
то площа її знаходиться по формулі
 ,
,
де
 і
і
 визначаються з рівності
визначаються з рівності
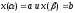 .
.
Приклад
9.7.1.
Обчислити площу фігури, що обмежена
віссю
 і графіком функції
і графіком функції
 при
при
 .
.

(рис.178)
○ Фігура
має вигляд, зображений на рис. 178. Знаходимо
її площу
 :
: ●
●
Приклад
9.7.2.
Обчислити площу фігури, що обмежена
еліпсом
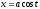 ,
, .
.
○ Знайдемо
спочатку
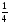 площіS.
Тут
площіS.
Тут
 змінюється від 0 до
змінюється від 0 до ,
отже,
,
отже, змінюється від
змінюється від до 0 (див. рис. 179).
до 0 (див. рис. 179).

(рис.179)
Знаходимо:
 .
.

Таким
чином,
 .
Значить
.
Значить![]() .●
.●
Знайдемо
площу S
криволінійного
сектора,
тобто плоскої фігури, обмеженої
неперервною лінією
 і двома променями
і двома променями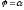 і
і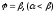 ,
де
,
де і
і![]() —полярні
координати (див. рис. 180). Для розв’язання
задачі використовуємо другу схему—метод
диференціала.
—полярні
координати (див. рис. 180). Для розв’язання
задачі використовуємо другу схему—метод
диференціала.

(рис.180)
Вважатимемо частину шуканої площі S як функцію кута
 ,
тобто
,
тобто
 ,
де
,
де
 (якщо
(якщо
 ,
то
,
то
 ,
якщо
,
якщо
 ,
то
,
то
 ).
).Якщо поточний полярний кут
 отримає приріст
отримає приріст
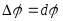 ,
то й приріст площі
,
то й приріст площі
 дорівнює площі «елементарного
криволінійного сектора»
дорівнює площі «елементарного
криволінійного сектора»
 .
.
Диференціал
 є головною частиною приросту
є головною частиною приросту
![]() при
при
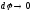 і дорівнює площі кругового сектора
і дорівнює площі кругового сектора
 (на рис. вона заштрихована) радіусу
(на рис. вона заштрихована) радіусу
![]() з центральним кутом
з центральним кутом
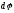 .
Тому
.
Тому
 .
.
Інтегруючи отриману рівність в межах
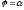 і
і
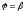 ,
отримаємо шукану
,
отримаємо шукану
площу
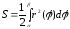 .
.
Приклад
9.7.3.
Знайти площу фігури, що обмежена
«трьохпелюстковою трояндою»
 (див. рис. 181).
(див. рис. 181).

(рис.181)
○
Знайдемо
спочатку площу половини одного листка
«троянди», тобто
 частини всієї площі фігури:
частини всієї площі фігури:
 ,
тобто
,
тобто
 .
Отже,
.
Отже,
 .●
.●
Якщо плоска фігура має «складну» форму, то промінням, що виходить з полюса, її слід розбити на криволінійні сектори, до яких застосувати одержану формулу для знаходження площі. Так, для фігури, зображеної на рис. 182, маємо:

(рис.182)
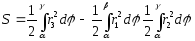 .
.
