Тема 9.5.Обчислення визначеного інтеграла

1. 9.5.1. Формула Ньютона-Лейбніца.

Простим і зручним методом обчислення визначеного інтеграла від неперервної функції є формула Ньютона-Лейбніца:

.

Застосовують цей метод у всіх випадках, коли може бути знайдена первісна функції 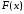для підінтегральної функції .

Наприклад. .

При обчисленні визначених інтегралів широко використовується метод заміни змінної і метод інтегрування по частинах.

2. 9.5.2. Інтегрування підстановкою (заміни змінної).

Нехай для обчислення інтеграла від неперервної функції зроблена підстановка .

Теорема 9.5.1. Якщо:

1. Функція і її похіднанеперервні при;

2. Множиною значень функції при є відрізок ;

3. і ,

то

. (9.5.1)

□ Нехай є первісною для на відрізку . Тоді по формулі Ньютона-Лейбніца . Оскільки , то є первісною для функції . Тому по формулі Ньютона-Лейбніца маємо .■

Формула (9.5.1) називається формулою заміни змінної в визначеному інтегралі.

Відзначимо, що:

1. при обчисленні визначеного інтеграла методом підстановки повертатися до старої змінної не потрібно;

2. часто замість підстановки застосовують підстановку ;

3. не слід забувати міняти межі інтегрування при заміні змінних!

Приклад 9.5.1. Обчислити .

○ Покладемо , тоді . Якщо , то ; якщо , тоо. Тому

.●

4. 9.5.3. Інтегрування частинами.

Теорема 9.5.2. Якщо функції імають неперервні похідні на відрізку, то має місце формула

. (9.5.2)

□ На відрізку має місце рівність. Отже, функціяє первісною для неперервної функції. Тоді по формулі Ньютона-Лейбніца маємо:

.

Отже,

.■

Формула (39.2) називається формулою інтегрування по частинах для визначеного інтеграла.

Приклад 9.5.2. Обчислити .

○ Покладемо .

Використовуючи формулу (9.5.2), отримаємо

.

Приклад 9.5.3. Обчислити інтеграл .

○ Розв’язання: Інтегруємо по частинах. Покладемо

.

Тому

. ●

5. 9.5.4. Інтегрування парних і непарних функцій в симетричних межах.

Нехай функція неперервна на відрізку , симетричному відносно точки . Доведемо, що

(9.5.3)

Розіб'ємо відрізок інтегрування на частини і . Тоді за властивістю аддитивності

. (9.5.4)

В першому інтегралі зробимо підстановку. Тоді

(згідно з властивістю: «визначений інтеграл не залежить від позначення змінної інтегрування»). Повертаючись до рівності (9.5.4), отримаємо

. (9.5.5)

Якщо парна ((), то ; якщо функція непарна ((), то .

Отже, рівність (9.5.5) приймає вигляд (9.5.3).

Завдяки доведеній формулі можна, наприклад, відразу, не проводячи обчислень, сказати, що

, .

Тема 9.6. Невласні інтеграли.

Визначений інтеграл , де проміжок інтегруванняскінчений, а підінтегральна функціянеперервна на відрізку, називають йоговласним інтегралом.

Розглянемо так звані невласні інтеграли, тобто визначений інтеграл від неперервної функції, але з нескінченним проміжком інтегрування або визначений інтеграл з скінченим проміжком інтегрування, але від функції, що має на ньому нескінченний розрив.

9.6.1. Інтеграл з нескінченним проміжком інтегрування

Нехай функція неперервна на проміжку . Якщо існує скінчена границя , то її називають невласним інтегралом першого роду і позначають .

Таким чином, по означенню

.

В цьому випадку говорять, що невласний інтеграл збіжний.

Якщо ж вказана границя не існує або вона нескінченна, то говорять, що інтеграл розбіжний.

Аналогічно означається невласний інтеграл на проміжку :

.

невласний інтеграл з двома нескінченними межами визначається формулою , де — довільне число.

В цьому випадку інтеграл зліва збіжний лише тоді, коли збіжні обидва інтеграли справа. Відзначимо, що якщо неперервна функція на проміжкуі інтегралзбіжний, то він виражає площу нескінченно довгої криволінійної трапеції (див. рис. 172).

(рис.172)

Приклад 9.6.1. Обчислити невласні інтеграли або встановити їх розбіжність: 1) ; 2); 3) .

○ 1) , інтеграл збіжний;

2), інтеграл розбіжний, оскільки при границя не існує.

3), інтеграл розбіжний. ●

В деяких задачах немає необхідності обчислювати інтеграл; достатньо лише знати, чи збіжний він чи ні.

Наведемо без доведення деякі ознаки збіжності.

Теорема 9.6.1 (ознака порівняння). Якщо на проміжку неперервні функціїізадовольняють умову, то із збіжності інтеграласлідує збіжність інтеграла, а з розбіжності інтеграласлідує розбіжність інтеграла.

Приклад 9.6.2. Чи збіжний інтеграл

○ При маємо . Але інтеграл збіжний. Отже, інтеграл також збіжний (і його значення менше 1). ●

Теорема 9.6.2. Якщо існує границя , то інтеграли і одночасно обидва збіжні або обидва розбіжні (тобто поводяться однаково в значенні збіжності).

Приклад 9.6.3. Дослідити збіжність інтеграла .

○ Інтеграл збіжний, оскільки інтегралзбіжний і

. ●