
- •Змістовий модуль 9
- •Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції
- •Робота змінної сили
- •Тема 9.3. Формула Ньютона-Лейбніца
- •Розглянемо тотожність
- •Перетворимо кожну різницю в дужках по формулі Лагранжа
- •Отримаємо
- •Тема 9.4. Основні властивості визначеного інтеграла
- •Так, наприклад, якщо , то
- •□ По формулі Ньютона-Лейбніца маємо
- •Тема 9.5.Обчислення визначеного інтеграла
- •9.5.1. Формула Ньютона-Лейбніца.
- •9.5.2. Інтегрування підстановкою (заміни змінної).
- •Теорема 9.5.1. Якщо:
- •9.5.3. Інтегрування частинами.
- •9.6.2. Інтеграл від розривної функції (невласний інтеграл другого роду)
- •Приклад 9.6.5. Чи збіжний інтеграл
- •Тема 9.7. Геометричні і фізичні застосування визначеного інтеграла
- •9.7.1. Схеми застосування визначеного інтеграла
- •9.7.2. Обчислення площ плоских фігур
- •9.7.3. Обчислення довжини дуги плоскої кривої.
- •Якщо рівняння кривої задано в параметричній формі
- •9.7.4. Обчислення об'єму тіла. Обчислення об'єму тіла за відомими площами паралельних перетинів
- •Об'єм тіла обертання
- •9.7.5. Обчислення площі поверхні обертання.
- •Приклад 9.7.9. Дано циклоїда
- •9.7.6. Механічне застосування визначеного інтеграла. Робота змінної сили
- •Тема 9.8. Наближене обчислення визначеного інтеграла
- •9.8.1. Формула прямокутників.
- •9.8.2. Формула трапецій.
- •9.8.3. Формула парабол (Сімпсона).
Тема 9.4. Основні властивості визначеного інтеграла
Розглянемо
основні властивості визначеного
інтеграла, вважаючи підінтегральну
функцію інтегрованою на відрізку
 .
При виведенні властивостей
використовуватимемо означення інтеграла
і формулу Ньютона-Лейбніца.
.
При виведенні властивостей
використовуватимемо означення інтеграла
і формулу Ньютона-Лейбніца.
Якщо
 — постійне число і функція
— постійне число і функція
 інтегрована на
інтегрована на

то
постійний множник
 можна виносити за знак визначеного
інтеграла.
можна виносити за знак визначеного
інтеграла.
 (9.4.1)
(9.4.1)
Складемо
інтегральну суму для функції
 .
Маємо :
.
Маємо :
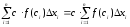 .
.
Тоді
 .
Звідси випливає, що функція
.
Звідси випливає, що функція
 інтегрована на
інтегрована на
 і справедлива формула (9.4.1).
і справедлива формула (9.4.1).
Якщо функції
 і
і інтегровані на
інтегровані на ,
тоді інтегрована на
,
тоді інтегрована на їх сума і
їх сума і
 (9.4.2)
(9.4.2)
тобто інтеграл від суми рівний сумі інтегралів.

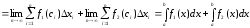 .
.
Властивість (2) розповсюджується на суму будь-якого скінченного числа доданків.
 .
Цю властивість можна прийняти за
означенням. Ця властивість також
підтверджується формулою Ньютона-Лейбніца.
.
Цю властивість можна прийняти за
означенням. Ця властивість також
підтверджується формулою Ньютона-Лейбніца.
 .
.
Якщо функція
 інтегрована на
інтегрована на
 і
і
 ,
то
,
то
 (9.4.3)
(9.4.3)
тобто інтеграл по всьому відрізку дорівнює сумі інтегралів по частинах цього відрізка. Цю властивість називають аддитивністю визначеного інтеграла (або властивістю аддитивності).
При
розбитті відрізка
 на частини включимо точку
на частини включимо точку в число точок поділу (це можна зробити
зважаючи на незалежність границі
інтегральної суми та способу розбиття
відрізка
в число точок поділу (це можна зробити
зважаючи на незалежність границі
інтегральної суми та способу розбиття
відрізка на частини). Якщо
на частини). Якщо
 ,
то інтегральну суму можна розбити на
дві суми:
,
то інтегральну суму можна розбити на
дві суми:
 .
.
Кожна
з написаних сум є інтегральною відповідно
для відрізків
 ,,
,, ,,
,, .
Переходячи до границі в останній рівності
при
.
Переходячи до границі в останній рівності
при
 ,
отримаємо рівність (38.3).
,
отримаємо рівність (38.3).
Властивість
(4) справедлива при будь-якому розташуванні
точок
 (вважаємо, що функція
(вважаємо, що функція інтегрується на більшому з відрізків).
інтегрується на більшому з відрізків).
Так, наприклад, якщо , то
 .
.
Звідси

(використані властивості (3) і (4)).
«Теорема про середнє». Якщо функція
 неперервна на відрізку
неперервна на відрізку
 ,
то існує точка
,
то існує точка
 така, що
така, що
 .
.
□ По формулі Ньютона-Лейбніца маємо
 ,
,
де
 .
Застосовуючи до різниці
.
Застосовуючи до різниці
 теорему Лагранжа (теорему про скінчевий
приріст функції), отримаємо
теорему Лагранжа (теорему про скінчевий
приріст функції), отримаємо
 .■
.■
Властивість
(5) («Теорема про середнє») при
 має простий геометричний зміст: значення
визначеного інтеграла дорівнює, при
деякому
має простий геометричний зміст: значення
визначеного інтеграла дорівнює, при
деякому
 ,
площі прямокутника з висотою
,
площі прямокутника з висотою
 і основою
і основою
 (див. рис. 170).
(див. рис. 170).

(рис.170)
Число
 називаєтьсясереднім
значенням функції
називаєтьсясереднім
значенням функції
 на відрізку
на відрізку
 .
.
Якщо функція
 зберігає знак на відрізку
зберігає знак на відрізку
 ,
де
,
де
 ,
то інтеграл
,
то інтеграл
 має той же знак, що і функція. Так, якщо
має той же знак, що і функція. Так, якщо
 на відрізку
на відрізку
 ,
то
,
то
 .
.
За «теоремою про середнє» (властивість (5))
 ,
де
,
де
 .
А оскільки
.
А оскільки
 для всіх
для всіх
 ,
то і
,
то і
 .
.
Тому
 ,
тобто
,
тобто
 .
.
Нерівність між неперервними функціями на відрізку
 ,
,
 можна інтегрувати. Так, якщо
можна інтегрувати. Так, якщо
 при
при
 ,
то
,
то
 .
.
Оскільки
 ,
то при
,
то при
 ,
згідно властивості (6), маємо
,
згідно властивості (6), маємо
 .
.
Або, згідно властивості (2)
 ,
тобто
,
тобто
 .
.
Відзначимо, що диференціювати нерівності не можна.
Оцінка інтеграла. Якщо т і М — відповідно найменше і найбільше значення функції
 на відрізку
на відрізку ,
, ,
то
,
то
 .
.
Застосовуючи до крайніх інтегралів властивість (5), отримаємо
 .
.
Якщо
 ,
та властивість (8) ілюструється геометрично:
площа криволінійної трапеції вкладена
між площами прямокутників, основою яких
є
,
та властивість (8) ілюструється геометрично:
площа криволінійної трапеції вкладена
між площами прямокутників, основою яких
є ,
а висоти рівні
,
а висоти рівні і
і (див. рис.171).
(див. рис.171).

(рис.171)
Модуль визначеного інтеграла не перевершує інтеграла від модуля підінтегральної функції:
 .
.
Застосовуючи
властивість (7) до очевидних нерівностей
 ,
отримаємо
,
отримаємо
 .
.
Звідси
слідує, що  .
.
Похідна визначеного інтеграла по змінній
верхній межі дорівнює підінтегральній функції, в якій змінна інтегрування замінена цією межею, тобто
 .
.
По
формулі Ньютона-Лейбніца маємо:
 .
.
Отже,
 .
.
Це означає, що визначений інтеграл із змінною верхньою межею є одна з первісних підінтегральних функцій.
