Тема 9.2. Геометричний і фізичний зміст визначеного інтеграла Площа криволінійної трапеції

Нехай на відрізку задана неперервна функція. Фігура, обмежена зверху графіком функції, а знизу — віссюОх, збоку — прямими і, називаєтьсякриволінійною трапецією. Знайдемо площу цієї трапеції.

(рис.168)

Для цього відрізок точками, розіб'ємо на частинних відрізків(див. рис. 168). В кожному частинному відрізкувізьмемо довільну точку і обчислимо значення функції в ній, тобто .

Помножимо значення функції на довжину відповідного частинного відрізка. Добуток дорівнює площі прямокутника з основою і висотою . Сума всіх таких добутків

дорівнює площі ступінчатої фігури і приблизно дорівнює площі криволінійної трапеції:

, тобто .

Із зменшенням всіх величин точність наближення криволінійної трапеції ступінчатої фігури і точність одержаної формули збільшуються. Тому за точне значення площікриволінійній трапеції приймається границя, до якої прямує площа ступінчатої фігури, колинеобмежено зростає так, що:

, тобто .

Отже, визначений інтеграл від невід’ємної функції чисельно рівний площі криволінійної трапеції.

В цьому і полягає геометричний зміст визначеного інтеграла.

Робота змінної сили

Нехай матеріальна точка М переміщається під дією сили , направленої уподовж осіі має змінну величину, де— абсциса рухомої точки М.

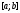Знайдемо роботу сили по переміщенню точки М вздовж осі з точки в точку . Для цього розіб'ємо відрізок точкаминачастинних відрізків. Сила діюча на відрізку, змінюється від точки до точки. Але якщо довжина відрізка 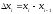достатньо риса, то сила 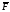на цьому відрізку змінюється трохи. Її можна приблизно вважати постійною і рівною значенню функції в довільно обраній точці . Тому робота, виконана цією силою на відрізку , рівна добутку .(Як робота постійної сили на ділянці .)

Наближене значення роботи сили на всьому відрізку є

. (9.2.1)

Ця наближена рівність тим точніша, чим менша довжина . Тому за точне значення роботи приймається границя суми (9.2.1) за умови, що найбільша довжина частинних відрізків прямує до нуля:

.

Отже, робота змінної сили , величина якої є неперервна функція , що діє на відрізку , дорівнює визначеному інтегралу від величини сили, узятому по відрізку .

В цьому полягає фізичний зміст визначеного інтеграла.

Аналогічно можна показати, що шлях , пройдений точкою за проміжок часу від до 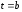, дорівнює визначеному інтегралу від швидкості :

;

маса неоднорідного стержня на відрізку дорівнює визначеному інтегралу від густини : .

Тема 9.3. Формула Ньютона-Лейбніца

Нехай функція інтегрована на відрізку .Точки розриву 1 роду

Теорема 9.3.1 Якщо функція неперервна на відрізкуі— яка-небудь її первісна, то має місце формула

. (9.3.1)

□ Розіб'ємо відрізок 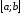точками на частинних відрізків , так як це показано на рис.169.

(рис.169)

Розглянемо тотожність

.

Перетворимо кожну різницю в дужках по формулі Лагранжа

.

Отримаємо

.

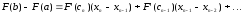
тобто

,

де є деяка точка інтервалу . Так як функція неперервна на 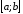. Тому існує границя інтегральної суми, що дорівнює визначеному інтегралу від на .

Переходячи в рівності (9.3.2) до границі при , отримаємо

,

тобто

.■

Рівність (9.3.1) називається формулою Ньютона-Лейбніца.

Якщо ввести позначення , то формулу Ньютона-Лейбніца можна переписати так:

.

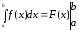Формула Ньютона–Лейбница дає зручний спосіб обчислення визначеного інтеграла. Щоб обчислити визначений інтеграл від неперервної функції на відрізку, треба знайти її первісну функціюі узяти різницюзначень цієї первісної на кінцях відрізка.

Приклад 9.3.1 Обчислити інтеграл .

○

.●

Приклад 9.3.2 Обчислити інтеграл .

○●