Тема 9.8. Наближене обчислення визначеного інтеграла

Нехай потрібно знайти визначений інтеграл від неперервної функції . Якщо можна знайти первісну функції , то інтеграл обчислюється по формулі Ньютона-Лейбніца:

Але знаходження первісної функції іноді досить складне, так відомо, не для всякої неперервної функції її первісна виражається через елементарні функції. В цих і інших випадках (наприклад, функція задана графічно або таблично) вдаються до наближених формул, за допомогою яких визначений інтеграл знаходиться з будь-яким ступенем точності.

Розглянемо три найбільш вживані формули наближеного обчислення визначеного інтеграла - формулу прямокутників, формулу трапецій, формулу парабол (Сімпсона), основані на геометричному значенні визначеного інтеграла.

9.8.1. Формула прямокутників.

Нехай на відрізку , задана неперервна функція . Потрібно обчислити інтеграл чисельно рівний площі відповідної криволінійної трапеції. Розіб'ємо основу цієї трапеції, тобто відрізок, нарівних частин (відрізків) довжини (крок розбиття) за допомогою точокМожна записати, що, де(див. рис. 200).

(рис.200)

В середині кожного такого відрізка побудуємо ординату графіка функції . Прийнявши цю ординату за висоту, побудуємо прямокутник з площею .

Тоді сума всіх площ прямокутників дає площу ступінчатої фігури, що є наближеним значенням шуканого визначеного інтеграла

. (9.8.1)

Формула (9.8.1) називається формулою середніх прямокутників.

Абсолютна похибка наближеної рівності (9.8.1.1) оцінюється за допомогою наступної формули:

де - найбільше значення на відрізку ,

.

Відзначимо, що для лінійної функції формула (9.8.1) дає точну відповідь, оскільки в цьому випадку.

9.8.2. Формула трапецій.

Формулу трапецій отримують аналогічно формулі прямокутників: на кожному частковому відрізку криволінійна трапеція замінюється звичайною.

Розіб'ємо відрізок 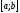на рівних частин довжини . Абсциси точок поділу (рис..201). Нехайвідповідні їм ординати графіка функції. Тоді розрахункові формули для цих значень матимуть вигляд.

(рис.201)

Замінимо криву ламаною лінією, ланки якої сполучають кінці ординаті. Тоді площа криволінійної трапеції приблизно дорівнює сумі площ звичайних трапецій з підставамиі висотою

або

. (9.8.2)

Формула (9.8.2) називається формулою трапецій.

Абсолютна похибка наближення, отриманого по формулі трапецій, оцінюється за допомогою формули , де . Знову для лінійної функції формула (9.8.2) – точна.

9.8.3. Формула парабол (Сімпсона).

Якщо замінити графік функції на кожному відрізкурозбиття не відрізками прямих, як в методах трапецій і прямокутників, а дугами парабол, то отримаємо більш точну формулу наближеного обчислення інтеграла.

Заздалегідь знайдемо площу криволінійної трапеції, обмеженої зверху графіком параболи, збоку – прямимиі знизу – відрізком

Нехай парабола проходить через три точки , де — ордината параболи в точці ; — ордината параболи в точці ; — ордината параболи в точці (див.рис. 202).

(рис.202)

Площа дорівнює

(9.8.3)

Виразимо цю площу через . З рівності для ординат знаходимо, що . Підставляючи ці значення і в рівність (42.3), отримаємо

Отримаємо тепер формулу парабол для обчислення інтеграла

Для цього відрізок розіб'ємо нарівних частин (відрізків) завдовжкиточкамиВ точках поділуобчислюємо значення підінтегральної функціїде(див.рис.203).

(рис.203)

Замінюємо кожну пару сусідніх елементарних криволінійних трапецій з основами, рівними , однією елементарною параболічною трапецією з основою, рівною. На відрізкупарабола проходить через три точки. Використовуючи формулу (9.8.3), знайдемо

Аналогічно знайдемо

Склавши отриману рівність, маємо

або

(9.8.4)

Формула (9.8.4) називається формулою парабол (або Сімпсона).

Абсолютна похибка обчислення по формулі (9.8.4) оцінюється співвідношенням

де .

Відзначимо, що формула (9.8.4) дає точне значення інтеграла у всіх випадках, коли — многочлен, степінь якого менше або дорівнює трьом (тоді ).

Приклад 9.8.1. Обчислити , розбивши відрізок інтегрування на 4 частини.

○ Маємо: ,

(див.рис.204.)

(рис.204)

а) по формулі прямокутників:

тобто

б) по формулі трапеції:

, тобто ;

в) по формулі парабол:

тобто

Точне значення інтеграла

Абсолютні похибки відповідних формул такі а) 0,125; би) 0,25; в) 0.●

60