
- •Міністерство освіти і науки україни
- •1. Подвійний інтеграл, його властивості. Обчислення подвійного інтеграла в декартових координатах
- •Властивості подвійного інтеграла
- •Обчислення подвійного інтеграла в декартових координатах
- •Зразки розв’язування задач
- •Рис 1.7
- •Завдання для самостійної роботи
- •2. Обчислення подвійного інтеграла в полярній системі координат. Застосування подвійних інтегралів до задач геометрії.
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3. Застосування подвійного інтеграла для деяких задач механіки
- •Момент інерції пластинки
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4. Обчислення криволінійних інтегралів першого та другого роду. Формула Гріна. Умови незалежності криволінійного інтеграла від шляху інтегрування
- •Властивості криволінійних інтегралів
- •Обчислення криволінійних інтегралів першого роду за плоскою областю
- •За плоскою областю
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •5. Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.
- •Види диференціальних рівнянь першого порядку:
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •7. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •9. Метод варіації довільних сталих.
- •Завдання для самостійного розв’язування
- •Література
- •Вища математика в прикладах та задачах Частина IV
- •49600, М. Дніпропетровськ – 5, пр. Гагаріна, 4
Зразки розв’язування задач
Приклад 1. Розв’язати рівняння:
![]() .
.
Розв’язання.
Це
рівняння є диференціальним рівнянням
з відокремлюваними змінними. Для того,
щоб відокремити змінні, поділимо обидві
частини рівняння на
![]() , а потім проінтегруємо його:
, а потім проінтегруємо його:
![]() ,
,
![]() ,
,
![]() .
.
Для того, щоб обчислити інтеграл, що знаходиться у правій частині, використаємо заміну змінної в невизначеному інтегралі:
![]() ,
,

Маємо:
![]() ,
або
,
або
![]() .
.
Повертаючись до старої змінної, дістанемо:
![]() ,
,
![]() загальний розв’язок рівняння.
загальний розв’язок рівняння.
Приклад 2. Знайти загальний розв’язок диференціального рівняння:
![]() .
.
Розв’язання.
Вважаючи,
що
![]() ,
маємо:
,
маємо:
![]() .
.
Помножимо
обидві частини на
![]() ,
а потім відокремимо змінні. Для цього
рівняння розділимо на
,
а потім відокремимо змінні. Для цього
рівняння розділимо на![]() :
:
![]() .
.
Після інтегрування отримаємо:
![]() ,
,
![]() ,
,
![]() загальний
розв’язок.
загальний
розв’язок.
Приклад 3. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Для
того, щоб відокремити змінні, треба
спочатку винести за дужки співмножники
в кожній з частин рівняння, тобто
![]() та
та![]() з лівої і правої частин рівняння
відповідно, а потім розділити рівняння
на
з лівої і правої частин рівняння
відповідно, а потім розділити рівняння
на![]() і проінтегрувати
і проінтегрувати

![]() ,
,
![]() ,
,
![]() ,
,
![]() загальний
розв’язок.
загальний
розв’язок.
Підставимо початкові умови в загальний розв’язок та отримаємо частинний розв’язок рівняння
![]() ,
,
![]() частинний
розв’язок.
частинний
розв’язок.
Приклад 4. Знайти частинний розв’язок рівняння
![]() .
.
Розв’язання.
Для
відокремлювання змінних у цьому рівнянні
розділимо його на
![]() .
Маємо:
.
Маємо:
![]() .
.
Проінтегруємо обидві частини рівняння та для обчислення інтегралів зробимо відповідні заміни змінних:
![]() ,
,
 ,
,
![]() ,
,
![]() ,
або
,
або
![]() ,
,
![]() або
або
![]() .
.
![]() загальний
розв’язок.
загальний
розв’язок.
Використаємо початкові умови і отримаємо частинний розв’язок рівняння:
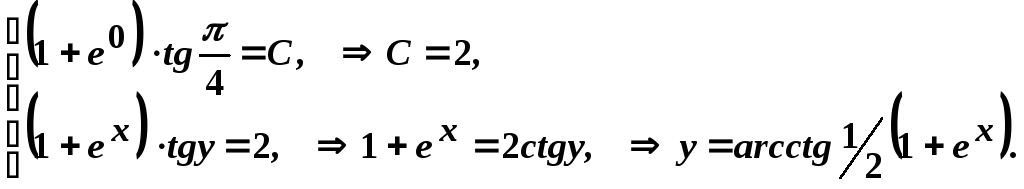
Приклад
5.
Записати рівняння кривої, яка проходить
через точку
![]() ,
кутовий коефіцієнт дотичної до якої у
кожній точці дорівнює
,
кутовий коефіцієнт дотичної до якої у
кожній точці дорівнює![]() .
.
Розв’язання.
Кутовий
коефіцієнт дотичної до кривої
![]() у кожній точці є
у кожній точці є![]() .
Маємо диференціальне рівняння з
відокремлюваними змінними:
.
Маємо диференціальне рівняння з
відокремлюваними змінними:
![]() .
.
Вважаємо,
що
![]() ,
та відокремлюючи змінні отримаємо:
,
та відокремлюючи змінні отримаємо:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() загальний
розв’язок рівняння.
загальний
розв’язок рівняння.
Підставимо координати точки, через яку проходить шукана крива, в отриманий розв’язок:
![]() .
.
Тоді
![]() є рівнянням цієї кривої.
є рівнянням цієї кривої.
Приклад 6. Розв’язати рівняння:
![]() .
.
![]()
Розв’язання.
Доведемо,
що це рівняння є однорідним. Нехай
![]() ,
тоді
,
тоді
![]() ,
,
![]() ,
тобто рівняння однорідне.
,
тобто рівняння однорідне.
Для
того, щоб перетворити його на рівняння
з відокремлюваними змінними, зробимо
підстановку:
![]() .
Отримаємо:
.
Отримаємо:
![]() ,
або
,
або
![]() ,
,
![]() .
.
Відокремлюючи змінні, маємо
![]() .
.
Після інтегрування отримаємо загальний інтеграл даного диференціального рівняння:
![]() ,
,
![]() .
.
Приклад 7. Знайти загальний розв’язок:
![]() .
.
Розв’язання.
Маємо:
![]() .
.
Функції
![]() та
та![]() є однорідними функціями другого виміру:
є однорідними функціями другого виміру:
![]() ;
;
![]() ,
,
Тобто початкове рівняння є однорідним.
Зробимо
підстановку
![]() ,
та зведемо це рівняння до рівняння з
відокремлюваними змінними:
,
та зведемо це рівняння до рівняння з
відокремлюваними змінними:
![]() ,
,
![]() ,
,
![]() ,
або
,
або
![]() .
.
Відокремимо змінні в останньому рівнянні:
![]() ;
;
![]() ;
;
 ;
;
 ,
або
,
або
 загальний
інтеграл даного рівняння;
загальний
інтеграл даного рівняння;
![]() ,
,
![]() ,
,
![]() ,
,
![]() загальний
розв’язок рівняння.
загальний
розв’язок рівняння.
Приклад 8. Розв’язати задачу Коші
![]() .
.
Розв’язання.
Це
рівняння є однорідним (перевірити
самостійно), тому після підстановки
![]() отримаємо рівняння з відокремлюваними
змінними:
отримаємо рівняння з відокремлюваними
змінними:
![]() ,
,
![]() ,
або
,
або
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Відокремимо змінні і проінтегруємо обидві частини рівняння:
![]() ,
,
або
![]() ,
,
![]() ,
,
![]() загальний
інтеграл.
загальний
інтеграл.
Використаємо початкові умови:
![]() .
.
Тоді
![]() ,
або
,
або![]() ,
або
,
або![]() розв’язок задачі Коші.
розв’язок задачі Коші.
Приклад 9. Знайти частинний розв’язок рівняння:
![]() при
при![]() .
.
Розв’язання.
Маємо:
![]() .
.
Це
однорідне рівняння. Зробимо підстановку
![]()
![]() та аналогічно попереднім прикладам
розв’яжемо отримане рівняння:
та аналогічно попереднім прикладам
розв’яжемо отримане рівняння:
![]() ,
,
![]() ,
,
![]() .
.
Для
обчислення інтеграла, що знаходиться
у лівій частині, використаємо заміну
змінної
![]() .
Маємо:
.
Маємо:
![]()
![]() .
.
Тоді,
загальний інтеграл рівняння має вигляд
![]() .
Знайдемо
.
Знайдемо![]() :
:
 .
.
![]() частинний розв’язок рівняння.
частинний розв’язок рівняння.
Приклад 10. Розв’язати рівняння:
![]() .
.
Розв’язання.
Це
рівняння є лінійним, і його розв’язок
будемо шукати у вигляді
![]() .
Тоді
.
Тоді![]()
Маємо:
![]() ,
,![]() .
.
Будемо вважати, що вираз в дужках у лівій частині рівняння дорівнює нулю. Тоді отримаємо систему диференціальних рівнянь з відокремлюваними змінними:

Знайдемо, спочатку, розв’язок першого рівняння. Для цього відокремимо змінні та проінтегруємо рівняння:
![]()
![]() .
.
Підставимо знайдений розв’язок в друге рівняння системи:
![]()
![]() .
.
Тоді, шуканий розв’язок лінійного рівняння матиме вигляд:
![]() .
.
Приклад 11. Розв’язати рівняння:
![]() .
.
Розв’язання.
Розв’язок
цього лінійного рівняння знаходимо у
вигляді
![]() .
Тоді
.
Тоді![]() .
Після підстановки цих виразів в лінійне
рівняння і розв’язування його аналогічно
попередньому дістанемо:
.
Після підстановки цих виразів в лінійне
рівняння і розв’язування його аналогічно
попередньому дістанемо:
![]() ,
,
![]() .
.

І.
![]()
![]() .
.
ІІ.
![]()
![]() .
.
Для останнього інтеграла використаємо підстановку:
 .
.
Дістанемо:
![]() .
.
Тоді загальний розв’язок лінійного рівняння буде мати вигляд:
![]() .
.
Приклад 12. Розв’язати рівняння:
![]() .
.
Розв’язання.
Розділимо
рівняння на
![]() ,
та розв’яжемо його аналогічно
попередньому:
,
та розв’яжемо його аналогічно
попередньому:![]() ;
;![]() ;
;
![]() ,
,![]() ,
,

І.
![]()
![]() .
.
ІІ.
![]()
![]() .
.
Отже,
![]() загальний розв’язок.
загальний розв’язок.
Приклад 13. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Розділимо
обидві частини рівняння на
![]() .
Дістанемо:
.
Дістанемо:
![]() .
.
Тоді
![]() ,
,
![]() ,
,
![]() .
.

І.
![]()
![]() ;
;
ІІ.
![]()
![]() .
.
Зробимо заміну змінної в інтегралі, що знаходиться праворуч.
 .
.
Для останнього інтеграла використаємо метод інтегрування частинами:

![]() .
.
Отже, повертаючись до старої змінної, отримаємо:
![]() .
.
Тоді, загальний розв’язок лінійного рівняння має вигляд:
![]() ,
або
,
або
![]() .
.
Підставимо
в цей вираз початкові умови: ![]() .
.
Отже
![]() частинний розв’язок лінійного рівняння.
частинний розв’язок лінійного рівняння.
Приклад 14. Розв’язати рівняння:
![]() .
.
Розв’язання.
Маємо рівняння Бернуллі, класичний вигляд якого буде:
![]() .
.
Метод
розв’язання – аналогічний до метода
розв’язання лінійних рівнянь. Тобто,
вважаючи, що
![]() ,
,![]() ,
дістанемо:
,
дістанемо:
![]() ,
,
![]() .
.
Нехай,
![]() ,
тоді
,
тоді![]() або
або![]() .
Таким чином, одержимо систему рівнянь
з відокремлюваними змінними:
.
Таким чином, одержимо систему рівнянь
з відокремлюваними змінними:

І.
![]()
![]() .
.
ІІ.
![]() .
.
Для
останнього інтеграла використаємо
заміну змінної
 .
Дістанемо:
.
Дістанемо:![]()
![]() .
.
Загальний розв’язок рівняння Бернуллі матиме вигляд:
![]() ,
або
,
або
![]() .
.
Приклад 15. Розв’язати рівняння:
![]() .
.
Розв’язання.
Перепишемо це рівняння Бернуллі у класичному вигляді:
![]() .
.
Загальний розв’язок рівняння Бернуллі буде
![]() .
.
Після підстановки цих виразів в початкове рівняння маємо:
![]() ,
,
![]() .
.

І.
![]() .
.
ІІ.
![]()
![]() .
.
Отже,
загальний розв’язок рівняння:
![]() .
.
Приклад 16. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Загальний
розв’язок рівняння Бернуллі будемо
шукати у вигляді:
![]() .
Тоді
.
Тоді
![]() ,
,
![]() ,
,
![]() .
.
 або
або

Тоді:
І.
 .
.
![]()
![]() .
.
ІІ.
![]()
![]() .
.
Отже загальний розв’язок рівняння Бернуллі має вигляд:
![]() .
.
Використовуючи
початкові умови знайдемо сталу
![]() :
:
![]() .
.
Маємо частинний розв’язок рівняння Бернуллі:
![]() .
.
Приклад 17. Розв’язати задачу Коші:
![]() .
.
Розв’язання.
Аналогічно
попередньому прикладу загальний
розв’язок задачі шукаємо у вигляді
![]() .
Маємо:
.
Маємо:


![]()

І.
![]()
![]() .
.
ІІ.
![]()

![]()
![]()
![]() .
.
Тоді, загальний розв’язок даного рівняння має вигляд:
![]() ,
або
,
або![]() .
.
Для
визначення частинного розв’язку
знаходимо
![]() ,
підставляючи початкові умови в загальний
розв’язок:
,
підставляючи початкові умови в загальний
розв’язок:
![]() .
.
Тому, частинний розв’язок має вигляд:
![]() .
.
