
- •Міністерство освіти і науки україни
- •1. Подвійний інтеграл, його властивості. Обчислення подвійного інтеграла в декартових координатах
- •Властивості подвійного інтеграла
- •Обчислення подвійного інтеграла в декартових координатах
- •Зразки розв’язування задач
- •Рис 1.7
- •Завдання для самостійної роботи
- •2. Обчислення подвійного інтеграла в полярній системі координат. Застосування подвійних інтегралів до задач геометрії.
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3. Застосування подвійного інтеграла для деяких задач механіки
- •Момент інерції пластинки
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •4. Обчислення криволінійних інтегралів першого та другого роду. Формула Гріна. Умови незалежності криволінійного інтеграла від шляху інтегрування
- •Властивості криволінійних інтегралів
- •Обчислення криволінійних інтегралів першого роду за плоскою областю
- •За плоскою областю
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •5. Звичайні диференціальні рівняння. Диференціальне рівняння першого порядку.
- •Види диференціальних рівнянь першого порядку:
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •6. Диференціальні рівняння вищих порядків. Диференціальні рівняння, що припускають зниження порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •7. Лінійні однорідні рівняння другого порядку зі сталими коефіцієнтами
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •9. Метод варіації довільних сталих.
- •Завдання для самостійного розв’язування
- •Література
- •Вища математика в прикладах та задачах Частина IV
- •49600, М. Дніпропетровськ – 5, пр. Гагаріна, 4
За плоскою областю
I.
Крива
![]() задана рівнянням
задана рівнянням![]() ,
а точки
,
а точки![]() і
і![]() задані кордина-
задані кордина-
тами
![]() :
:
 .
(4.4)
.
(4.4)
II.
Крива
![]() задається параметричними рівняннями
задається параметричними рівняннями

![]() .
.
 .
(4.5)
.
(4.5)
III.
Крива
![]() задається рівнянням
задається рівнянням
![]() ,
,![]() .
.
![]()
 .
(4.6)
.
(4.6)
Формула Гріна встановлює зв’язок між подвійним інтегралом по плоскій області й криволінійним інтегралом по контуру цієї області. Формула Гріна має вигляд:
![]() ,
,
де
Г
–
контур області
![]() функції
неперервні в області
функції
неперервні в області![]() ,
для яких існують неперервні частинні
похідні
,
для яких існують неперервні частинні
похідні![]() і
і![]() .
.
Нехай
функції
![]() визначені і неперервні в однозв’язній
обмеженій замкненій області
визначені і неперервні в однозв’язній
обмеженій замкненій області![]() площини
площини![]() .
Тоді величина криволінійного інтеграла
.
Тоді величина криволінійного інтеграла
![]()
не
залежить від шляху інтегрування, а лише
від початкової й кінцевої точок
інтегрування та від функцій
![]() і
і![]() ,
якщо буде виконуватися рівність:
,
якщо буде виконуватися рівність:
![]()
Зразки розв’язування задач
Приклад
1.
Обчислити криволінійний інтеграл
![]() ,
де
,
де![]() відрізок
прямої, яка сполучає точки
відрізок
прямої, яка сполучає точки![]() і
і![]() .
.
Розв’язання.
Рівняння прямої, якій задовольняють задані точки, знаходиться за формулою:
![]() ,
,
де
![]() задані
точки.
задані
точки.
Пряма
![]() має вигляд:
має вигляд:![]() або
або![]() .
Звідси
.
Звідси![]() .
.
За формулою (4.1) матимемо

![]() .
.
Приклад
2.
Обчислити криволінійний інтеграл
першого роду
![]() ,
де
,
де![]() коло
коло![]() .
.
Розв’язання.
Перейдемо
до полярних координат:
![]()
![]() .
Рівняння кривої
.
Рівняння кривої![]() набуває вигляду
набуває вигляду![]() ,
де
,
де![]() .
Для обчислення інтеграла застосуємо
формулу (4.3), оскільки
.
Для обчислення інтеграла застосуємо
формулу (4.3), оскільки![]() .
Отже
.
Отже
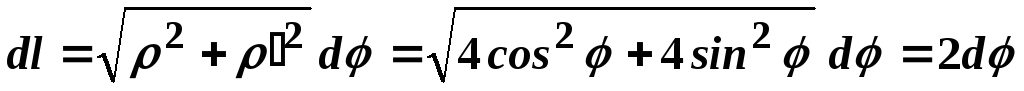 ;
;


![]() .
.
Приклад
3.
Обчислити криволінійний інтеграл
першого роду
![]() ,
де
,
де![]() дуга
циклоїди
дуга
циклоїди![]() між точками
між точками![]() та
та![]() .
.
Розв’язання.
Знайдемо
похідні функцій
![]() та
та![]() за параметром
за параметром![]() :
:
![]() .
.
За формулою (4.5) матимемо
![]()
![]()

![]() .
.
Приклад
4.
Обчислити криволінійний інтеграл
![]() ,
де
,
де![]() відрізок
прямої від точки
відрізок
прямої від точки![]() до точки
до точки![]() .
.
Розв’язання.
Запишемо
рівняння прямої, що проходить через
точки
![]() і
і![]() :
:
![]() .
.
Тоді
![]() .
Скористаємось формулою (4.4):
.
Скористаємось формулою (4.4):
![]()
![]() .
.
Приклад
5.
Обчислити інтеграл
![]() вздовж ламаної
вздовж ламаної![]() ,
де
,
де![]() і
і![]() .
.
Розв’язання.
Вздовж
ламаної
![]() на ділянці
на ділянці![]() маємо
маємо![]() і
і![]() ,
на ділянці
,
на ділянці![]()
![]() .
.
Тому, згідно з формулою (4.4), маємо:
![]()
![]() .
.
Приклад
6.
Обчислити інтеграл
![]() ,
де
,
де![]() частина
гіперболічної спіралі
частина
гіперболічної спіралі![]() від
від![]() до
до![]() .
.
Розв’язання.
Розглянемо
полярну систему координат:
![]() ,
,![]() .
Тоді
.
Тоді![]() .
.
За формулою (4.3) маємо

 .
.
Приклад
7.
За допомогою формули Гріна обчислити
криволінійний інтеграл
![]() ,
де
,
де![]() коло
коло![]() .
.
Розв’язання.
За
умовами задачі
![]() ;
;
![]() .
Отже
.
Отже
![]() .
.
За формулою Гріна
![]()
![]() .
.
Область
![]() коло
з центром в точці
коло
з центром в точці![]() і радіусом
і радіусом![]() .
Рівняння кола має вигляд:
.
Рівняння кола має вигляд:
![]() .
.
Перейдемо
до полярних координат з полюсом у центрі
![]() .
Рівняння, яке зв’язує
.
Рівняння, яке зв’язує![]() і полярні координати
і полярні координати![]() з полюсом у точці
з полюсом у точці![]() ,
має вигляд:
,
має вигляд:![]() .
.
Таким
чином,
![]()
![]()
![]() .
.
Приклад
8.
Чи залежить криволінійний інтеграл
від шляху інтегрування
![]() ?
?
Розв’язання.
За
умовами задачі:
![]() .
Знайдемо часткові похідні
.
Знайдемо часткові похідні![]() і
і![]() :
:![]() .
.
Отже, інтеграл залежить від шляху інтегрування.
Завдання для самостійної роботи
I. Обчислити криволінійні інтеграли:
а)
![]() де
де![]() відрізок
прямої між точками
відрізок
прямої між точками![]() і
і![]() ;
;
б)
![]() ,
де
,
де![]() прямокутник
з вершинами
прямокутник
з вершинами![]()
![]() ;
;
в)
![]() ,
де
,
де![]() коло
коло![]() ;
;
г)
![]() де
де![]() арка
циклоїди
арка
циклоїди![]()
![]()
![]() ;
;
д)![]() ,
де
,
де![]() верхня
половина еліпса
верхня
половина еліпса![]() по ходу стрілки годинника;
по ходу стрілки годинника;
е)
![]() ,
де
,
де![]() лінія
лінія![]() від точки
від точки![]() до точки
до точки![]() .
.
II. За допомогою формули Гріна обчислити криволінійний інтеграл
![]() ,
де
,
де
![]() коло
коло![]() .
.
III. Вказати криволінійний інтеграл по координатах, який не залежить від
шляху інтегрування
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
