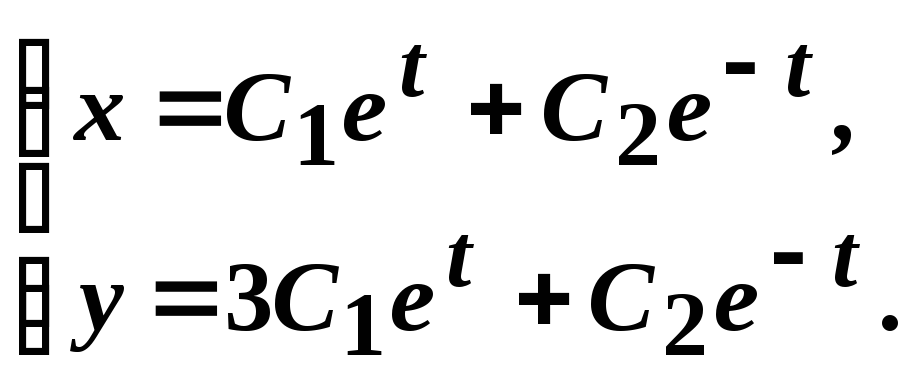8. Лінійні неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами із спеціальною правою частиною

Розглянемо лінійне неоднорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами:

.

Якщо права частина лінійного неоднорідного рівняння є функцією спеціального вигляду, то рівняння можна розв’язатиметодом невизначених коефіцієнтів, і загальний розв’язок має вигляд:

,

де загальний розв’язок відповідного однорідного рівняння,частинний розв’язок неоднорідного рівняння, який залежить від функціїта коренів характеристичного рівняння.

Можливі такі випадки:

1. Нехай , демногочлен степеня, тобто

, тоді:

а) якщо , тоді частинний розв’язок обираємо у вигляді, демногочлен ступенюз невідомими коефіцієнтами, тобто, якщо

,

,

,

;

б) якщо , тоді;

в) якщо , тоді.

Зауваження 1. Для знаходження невідомих коефіцієнтів многочлена треба підставити функціюта її похідні першого та другого порядку в вихідне рівняння та прирівняти коефіцієнти при однакових ступеняхз обох його сторін. Таким чином, дістанемо систему лінійних алгебраїчних рівнянь, з якої визначимо невідомі коефіцієнти.

2. Нехай , демногочлени степенівта, тоді існують такі випадки:

а) якщо , тоді, демногочлени ступенюз невідомими коефіцієнтами;

б) якщо , тоді.

Зауваження 2. У цьому випадку для знаходження невідомих коефіцієнтів многочленів тадіємо так само, але прирівнюємо коефіцієнти при, внаслідок чого знов дістанемо систему лінійних алгебраїчних рівнянь, з якої визначимо невідомі коефіцієнти.

Якщо, , детафункції спеціального вигляду, то частинний розв’язок неоднорідного лінійного рівняннямає вигляд

,

де тачастинні розв’язки лінійних неоднорідних рівнянь

тавідповідно.

Зразки розв’язування задач

Приклад 1. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Загальний розв’язок рівняння має вигляд , дезагаль-ний розв’язок відповідного однорідного рівняння. Характеристичне рівняннямає корені. Отже.

Частинний розв’язок неоднорідного рівняння залежить від вигляду правої частини (маємо).

Тоді . Для визначення невідомих коефіцієнтівтапідставимов початкове рівняння. Щоб це було можливим, знайдемо першу і другу похідні від частинного розв’язку:

Після підстановки в наше рівняння отримаємо

.

Розділимо рівняння на та приведемо подібні доданки. Маємо:

.

Прирівняємо коефіцієнти при в однакових ступенях:

Тобто, .

Отже, загальний розв’язок лінійного неоднорідного рівняння

.

Приклад 2. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Загальний розв’язок цього рівняння складається з двох компонентів . Характеристичне рівняння відповідного однорідного рівняннямає вигляд. Його корені:. Загальний розв’язок однорідного рівняння має вигляд:.

Враховуючи, що , тобто,, а також, що, дістанемо частинний розв’язок неоднорідного рівняння:

або .

Знаходимо:

,

Підставляючи в початкове рівняння, отримаємо:

Розділимо обидві частини на та приведемо подібні доданки:

.

Прирівняємо коефіцієнти при в однакових ступенях.

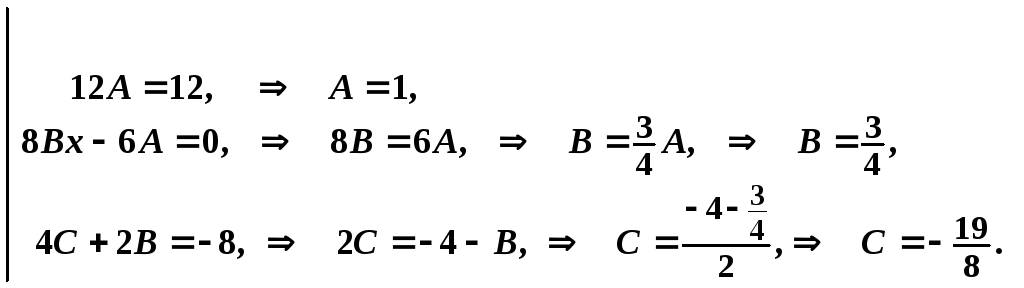
Тоді, .

Дістанемо загальний розв’язок лінійного неоднорідного рівняння у вигляді:

.

Приклад 3. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Аналогічно попередньому, маємо .

Характеристичне рівняння має однакові корені. Отже,.

, тобто,. Частинний розв’язок даного неоднорідного рівняння буде мати вигляд:

або

Після підстановки цих виразів в початкове рівняння, дістанемо

, або

.

Частинний розв’язок неоднорідного рівняння буде:

,

а загальний : .

Приклад 4. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Маємо: .

,

Отримаємо: .

Порівняємо коефіцієнти при тав обох частинах останнього рівняння:

Дістанемо систему рівнянь:

Розв’яжемо систему рівнянь за формулами Крамера:

;

;

.

Отже: , а

загальний розв’язок лінійного неоднорідного диференціального рівняння.

Приклад 5. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Маємо: .

, де . Загальний розв’язок однорідного рівняння.

Частинний розв’язок неоднорідного лінійного рівняння шукатимемо у вигляді :

,

,

Підставимо тав початкове рівняння та отримаємо:

Після низки арифметичних перетворень останнє рівняння набуває вигляду:

.

Порівняємо коефіцієнти при та:

Отримаємо систему рівнянь

яку розв’яжемо за формулами Крамера:

Тоді

Отже, маємо .

Загальний розв’язок неоднорідного рівняння дістанемо у вигляді:

.

Приклад 6. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Загальний розв’язок відповідного однорідного рівняння має вигляд. Оскільки, тобто, то частинний розв’язок неоднорідного рівняння буде:

,

,

Дістанемо:

Звідки, . Отже.

Загальним розв’язком лінійного неоднорідного рівняння буде функція .

Приклад 7. Знайти загальний розв’язок рівняння:

.

Розв’язання.

Загальний розв’язок відповідного однорідного рівняння має вигляд. Права частина початкового рівняння складається з двох доданків:, де. Тому частинний розв’язок лінійного неоднорідного рівняння теж складається з двох доданків:, детає частинними розв’язками рівнянь:

та

відповідно.

Аналогічно попередньому маємо:

,

,

.

Отримаємо:

, або

.

Отже, .

Тоді .

Звідки, . Отже,.

Загальний розв’язок початкового лінійного неоднорідного рівняння дістанемо у вигляді:

.

Приклад 8. Розв’язати задачу Коші:

.

Розв’язання.

Аналогічно попередньому маємо:

Отже, загальний розв’язок однорідного рівняння буде

.

.

,

,

.

Підставимо в початкове рівняння:

, або

.

Частинний розв’язок диференціального рівняння має вигляд: , а загальний розв’язок ‒.

Використаємо початкові умови, для цього знайдемо :

.

Маємо:

Отже, дістанемо розв’язок задачі Коші:

.

Приклад 9. Розв’язати задачу Коші:

.

Розв’язання.

Характеристичне рівняння відповідного однорідного диференціального рівняння має два рівних кореня . Отже,. Оскільки, права частина складається з суми двох різних функцій:, то кожній з них будуть відповідати частинні розв’язкита, а.

,

,

.

Маємо:

Розділимо це рівняння на :

.

Тобто, .

Знайдемо :

.

Прирівняємо коефіцієнти при та:

Отже: .

Дістанемо загальний розв’язок лінійного неоднорідного рівняння

.

Використаємо початкові умови, щоб знайти та, для цього треба знайти похідну від загального розв’язку:

.

Тоді:

Таким чином, розв’язок задачі Коші має вигляд:

.

Приклад 10. Розв’язати систему рівнянь:

Розв’язання.

Систему лінійних однорідних диференціальних рівнянь першого порядку із сталими коефіцієнтами розв’яжемо зведенням її до одного диференціального рівняння другого порядку. Для цього перше рівняння системи продиференцюємо по :

.

Замість підставимо праву частину другого рівняння системи:

.

З останнього виразу виключимо змінну . Для цього використаємо перше рівняння системи:

.

Отже, маємо:

, або

Тоді,

.

Отже, загальний розв’язок системи