
- •М.Д. Бабич, с.І. Куприков
- •1. Невизначений інтеграл
- •1.1. Первісна функція. Невизначений інтеграл.
- •1.2. Основні властивості невизначеного інтеграла
- •1.3. Таблиця основних невизначених інтегралів
- •Покажемо на прикладах, що наведені табличні інтеграли будуть вірні, коли - незалежній змінній і коли- диференційовній функції відx.
- •1.4. Основні методи інтегрування
- •1.5. Інтегрування раціональних дробів
- •1.6. Інтегрування простих ірраціональностей
- •1.7. Інтегрування тригонометричних функцій
- •1.8. Інтегрування деяких трансцендентних функцій
- •2. Визначений інтеграл
- •2.1. Визначений інтеграл як границя інтегральної суми
- •2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
- •2.3. Основні властивості визначеного інтеграла.
- •2.4. Методи обчислення визначених інтегралів
- •2.5. Застосування визначеного інтеграла
- •3. Функції двох змінних
- •3.1. Поняття функції двох змінних та їх геометричне зображення
- •3.2. Локальні екстремуми функції двох змінних
- •Дослідимо цю функцію всередині трикутника
- •4. Диференціальні рівняння
- •4.1. Основні поняття. Задача Коші.
- •4.2. Диференціальні рівняння першого порядку з відокремлюваними змінними
- •4.3. Лінійні диференціальні рівняння. Однорідні диференціальні рівняння
- •4.4. Диференціальні рівняння другого порядку
- •Диференціальні рівняння другого порядку, що допускають пониження порядку
- •4.5. Лінійні диференціальні рівняння другого порядку.
- •4.6. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.7. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •5. Числові та функціональні ряди
- •5.1. Числові ряди. Ознаки збіжності
- •5.2. Знакозмінні ряди
- •5.3. Функціональні ряди
- •5.4. Степеневі ряди. Радіус збіжності
- •5.5. Ряди Тейлора і Маклорена
- •Контрольна робота № 2
- •Рекомендована література
3. Функції двох змінних
3.1. Поняття функції двох змінних та їх геометричне зображення
Означення. Змінна величина z називається однозначною функцією змінних x і y , якщо кожній парі значень x і y із області їх допустимої зміни за певним правилом або законом ставиться у відповідність одне значення величини z. Функціональна залежність z від x і y записується у виді :
|
|
(3.1) |
Множина допустимих значень змінних x і y називається областю визначення функції z або областю допустимих значень (ОДЗ) аргументу.
Наприклад,
функція
![]() є многочлен цілий відносноx
і y.
Це означає, що ОДЗ є вся площина ХоУ;
є многочлен цілий відносноx
і y.
Це означає, що ОДЗ є вся площина ХоУ;
![]() - це є функція, область допустимих значень
якої визначає круг
- це є функція, область допустимих значень
якої визначає круг![]() .
.
Пара
значень x і
y
визначає на площині ХоУ точку
![]() а
а![]() - визначає аплікату відповідної точки
- визначає аплікату відповідної точки![]() .
Множина точок
.
Множина точок![]() ,
що відповідає множині точок
,
що відповідає множині точок![]() геометрично визначає деяку поверхню.
Тому кажуть, щоz
є функція точки
геометрично визначає деяку поверхню.
Тому кажуть, щоz
є функція точки
![]() і пишуть
і пишуть![]() .
.
Границя
функції. Число
А називається границею функції
![]() або
або![]() при
при![]() ,
якщо різниця
,
якщо різниця![]() -А
або
-А
або![]() -А
є нескінченно мала при
-А
є нескінченно мала при![]() або
або![]() при будь-якому способі прямування
точки Р до точки
при будь-якому способі прямування
точки Р до точки![]() .
Позначається це так:
.
Позначається це так:
 або
або
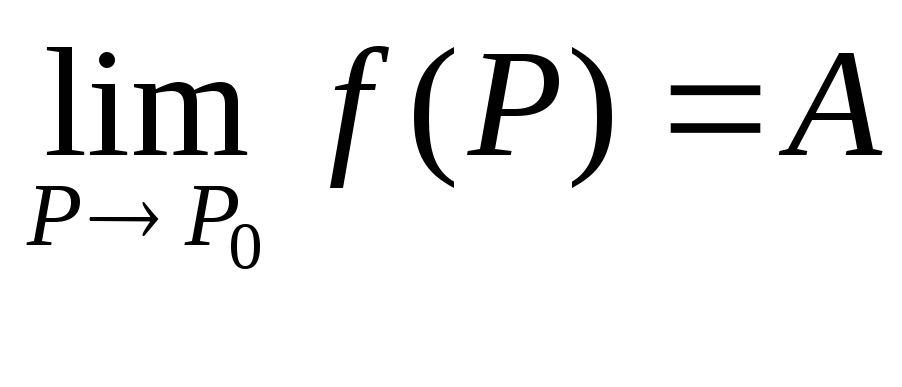 .
.
Неперервність
функції. Функція
![]() називається неперервною в точці
називається неперервною в точці![]() ,
якщо
,
якщо
 або
або
![]()
Функція
![]() називається неперервною в деякій
області, якщо вона неперервна в будь-якій
точці цієї області.
називається неперервною в деякій
області, якщо вона неперервна в будь-якій
точці цієї області.
Неперервна
в замкненій області функція
![]() досягає на ній своє найбільше і найменше
значення.
досягає на ній своє найбільше і найменше
значення.
Частинні
похідні 1-го порядку.
Нехай у функції
![]() зміннау
зберігає постійне значення, а змінюється
тільки х .
Тоді функцію
зміннау
зберігає постійне значення, а змінюється
тільки х .
Тоді функцію
![]() можна розглядати як функцію одногох
і ставити питання про
її приріст і похідну. Позначимо через
можна розглядати як функцію одногох
і ставити питання про
її приріст і похідну. Позначимо через
![]() прирістz,
який вона набуде за умови, що у
– стала, а х
набуде приросту
прирістz,
який вона набуде за умови, що у
– стала, а х
набуде приросту
![]() ,
тобто
,
тобто
![]() .
.
Похідну
отримаємо, якщо знайдемо відношення
![]() та його границю, при
та його границю, при![]() ,
тобто
,
тобто
![]() ;
;
Ця похідна, яка отримана за умови, що y залишається сталою, називається частинною похідною від z по х і позначається так:
![]() або
або
![]() або
або![]() .
.
Аналогічно визначається частинна похідна функції z по у за умови, що в цьому випадку змінна х залишається сталою, тобто
![]() або
або
![]() або
або![]() .
.
Правила
знаходження частинних похідних такі
самі, як і для похідних від функції
одної змінної з таким зауваженням: коли
шукається
![]() ,
тоу
вважається сталою величиною, а коли
шукається
,
тоу
вважається сталою величиною, а коли
шукається
![]() ,
тох
вважається сталою величиною.
,
тох
вважається сталою величиною.
Приклад.
Знайти
![]() і
і![]() ,
якщо
,
якщо![]()
![]() .
.
![]()
Повний
диференціал 1-го порядку.
Якщо функція
![]() має у точці
має у точці![]() неперервні частинні похідні, то її
повний приріст записується у вигляді
неперервні частинні похідні, то її
повний приріст записується у вигляді
|
|
(3.2) |
де
![]() при
при![]() .
Вираз
.
Вираз![]() представляє головну частину повного
приросту функції. Він називається
повним диференціалом функції і
позначається
представляє головну частину повного
приросту функції. Він називається
повним диференціалом функції і
позначається![]() .
Отже,
.
Отже,
|
|
(3.3) |
Якщо покласти у (3.3) послідовно z=x, а потім z=y , то одержимо:
![]() і
і
![]() і формула (3.3) набуде вигляду
і формула (3.3) набуде вигляду
|
|
(3.4) |
Із (3.2)
випливає, що при достатньо малих
![]() і
і![]() повний приріст функціїz
наближено дорівнює її
повному диференціалу, тобто
повний приріст функціїz
наближено дорівнює її
повному диференціалу, тобто
![]() .
Цей факт широко використовується при
наближених обчисленнях, оскільки
диференціал функції обчислюється
простіше, ніж її повний приріст.
.
Цей факт широко використовується при
наближених обчисленнях, оскільки
диференціал функції обчислюється
простіше, ніж її повний приріст.
Приклад.
Знайти значення повного диференціала
функції
![]() при
при![]() .
Скористаємось формулою (3.4). Для цього
знаходимо:
.
Скористаємось формулою (3.4). Для цього
знаходимо:![]()
![]() ;
тоді
;
тоді![]() =
=
![]() .
.
