
- •М.Д. Бабич, с.І. Куприков
- •1. Невизначений інтеграл
- •1.1. Первісна функція. Невизначений інтеграл.
- •1.2. Основні властивості невизначеного інтеграла
- •1.3. Таблиця основних невизначених інтегралів
- •Покажемо на прикладах, що наведені табличні інтеграли будуть вірні, коли - незалежній змінній і коли- диференційовній функції відx.
- •1.4. Основні методи інтегрування
- •1.5. Інтегрування раціональних дробів
- •1.6. Інтегрування простих ірраціональностей
- •1.7. Інтегрування тригонометричних функцій
- •1.8. Інтегрування деяких трансцендентних функцій
- •2. Визначений інтеграл
- •2.1. Визначений інтеграл як границя інтегральної суми
- •2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
- •2.3. Основні властивості визначеного інтеграла.
- •2.4. Методи обчислення визначених інтегралів
- •2.5. Застосування визначеного інтеграла
- •3. Функції двох змінних
- •3.1. Поняття функції двох змінних та їх геометричне зображення
- •3.2. Локальні екстремуми функції двох змінних
- •Дослідимо цю функцію всередині трикутника
- •4. Диференціальні рівняння
- •4.1. Основні поняття. Задача Коші.
- •4.2. Диференціальні рівняння першого порядку з відокремлюваними змінними
- •4.3. Лінійні диференціальні рівняння. Однорідні диференціальні рівняння
- •4.4. Диференціальні рівняння другого порядку
- •Диференціальні рівняння другого порядку, що допускають пониження порядку
- •4.5. Лінійні диференціальні рівняння другого порядку.
- •4.6. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.7. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •5. Числові та функціональні ряди
- •5.1. Числові ряди. Ознаки збіжності
- •5.2. Знакозмінні ряди
- •5.3. Функціональні ряди
- •5.4. Степеневі ряди. Радіус збіжності
- •5.5. Ряди Тейлора і Маклорена
- •Контрольна робота № 2
- •Рекомендована література
2.5. Застосування визначеного інтеграла
Обчислення
площ плоских фігур.
Згідно з трактовкою
геометричного змісту визначеного
інтеграла, якщо функція
![]() на відрізку
на відрізку![]() неперервна і
неперервна і![]() ,
то площу криволінійної трапеції,
обмеженої кривою
,
то площу криволінійної трапеції,
обмеженої кривою![]() ,
віссю
,
віссю![]() і ординатами
і ординатами![]() і
і![]() (рис. 1) обчислюють за формулою (2.2).
Криволінійна трапеція
(рис. 1) обчислюють за формулою (2.2).
Криволінійна трапеція![]() (рис. 1) в цьому випадку лежить над віссю
(рис. 1) в цьому випадку лежить над віссю![]() .
Якщо ж
.
Якщо ж![]() на
на![]() ,
та фігура
,
та фігура![]() буде лежати під віссю
буде лежати під віссю![]() і її площа буде дорівнювати площі
рівновеликої аналогічної фігури,
обмеженої зверху кривою
і її площа буде дорівнювати площі
рівновеликої аналогічної фігури,
обмеженої зверху кривою![]() .
Тоді згідно з формулою (2.2)
.
Тоді згідно з формулою (2.2)
|
|
(2.6) |
Об‘єднавши формули (2.5) і (2.6) в одну, одержимо
|
|
(2.7) |
Ця
формула залишається справедливою, якщо
функція
![]() на відрізку
на відрізку![]() змінює свій знак скінчене число раз.
Дійсно, нехай
змінює свій знак скінчене число раз.
Дійсно, нехай![]() є знакозмінна неперервна функція на
відрізку
є знакозмінна неперервна функція на
відрізку![]()
![]() .
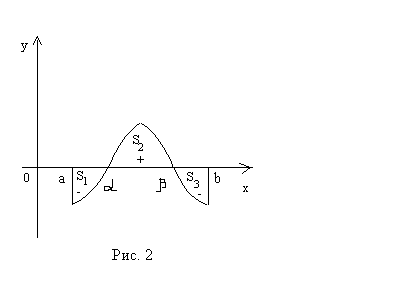
Наприклад (рис. 2),
.
Наприклад (рис. 2),![]() при
при![]() ,
,![]() при
при![]() і
і![]() при
при![]() .
Тоді згідно з властивістю 4 визначеного
інтеграла, та враховуючи його геометричний
зміст можна записати
.
Тоді згідно з властивістю 4 визначеного
інтеграла, та враховуючи його геометричний
зміст можна записати
|
|
(2.8) |
де
![]() - площі відповідних криволінійних
трапецій.
- площі відповідних криволінійних
трапецій.
Таким
чином, визначений інтеграл, в загальному
випадку, при
![]() є алгебраїчна сума площ відповідних
криволінійних трапецій, в якій площі
трапецій, розташованих над віссю
є алгебраїчна сума площ відповідних
криволінійних трапецій, в якій площі
трапецій, розташованих над віссю![]() ,
беруться із знаком плюс, а площі трапецій,
розташованих під віссю
,
беруться із знаком плюс, а площі трапецій,
розташованих під віссю![]() ,
із знаком мінус.
,
із знаком мінус.
Зауважимо, що площа заштрихованої на рис.2 фігури виражається інтегралом
![]() .
.
Очевидно,
щоб знайти площу такої фігури, потрібно
знайти нулі функції
![]() ,
тобто значення
,
тобто значення![]() і
і![]() ,
при яких
,
при яких![]() і взяти суму площ цих криволінійних
трапецій.
і взяти суму площ цих криволінійних
трапецій.
Приклад.
Знайти площу фігури, обмеженої кривою
![]() прямими
прямими![]() і
і![]() і віссю
і віссю![]() (рис. 3). Згідно з (2.8) та врахуванням того,
що
(рис. 3). Згідно з (2.8) та врахуванням того,
що![]() ,
,![]() ,
одержимо:
,
одержимо:

![]()
![]()
![]()
![]() кв.од.
кв.од.
Розглянемо
деякі інші випадки обчислення площ
криволінійних фігур. Нехай потрібно
обчислити площу фігури, обмеженої двома
неперервними лініями
![]() і
і![]() ,
при чому
,
при чому![]() та двома ординатами
та двома ординатами![]() і
і![]() (рис. 4).
(рис. 4).

Очевидно,
що шукану площу
![]() можна розглядати як різницю площ двох
криволінійних трапецій, обмежених цими
лініями і віссю
можна розглядати як різницю площ двох
криволінійних трапецій, обмежених цими
лініями і віссю![]() .
Отже
.
Отже
|
|
(2.9) |
Приклад.
Обчислити площу фігури, обмеженої
кривими
![]() ,
,![]() та прямими
та прямими![]() ,
,![]() .
.
Згідно з (2.9)
 .
.
До задачі
(2.9) зводиться і задача обчислення площі
криволінійної фігури, обмеженої лініями
![]() ,
,![]() ,
що перетинаються у двох точках. В цьому
випадку межі інтегрування визначаються
як абсциси точок перетину цих кривих і
знаходяться як розв‘язок рівняння
,
що перетинаються у двох точках. В цьому
випадку межі інтегрування визначаються
як абсциси точок перетину цих кривих і
знаходяться як розв‘язок рівняння![]() .
.
Приклад.
Знайти площу
![]() криволінійної фігури, обмеженої кривою
криволінійної фігури, обмеженої кривою![]() та прямою
та прямою![]() .
.
Межі
інтегрування знайдемо із рівняння
![]()
![]()
![]()
![]() кв.од.
кв.од.
Обчислення
об‘ємів тіл. Розглянемо
задачу обчислення об‘єму
![]() тіла за відомим законом зміни площі
його поперечного перерізу
тіла за відомим законом зміни площі
його поперечного перерізу![]() (рис. 5).
(рис. 5).

Нехай
![]() - деякий вибраний напрямок і
- деякий вибраний напрямок і![]() - площа поперечного перерізу площиною,
перпендикулярною осі
- площа поперечного перерізу площиною,
перпендикулярною осі![]() у
точці з абсцисою
у
точці з абсцисою![]() .
Функцію
.
Функцію![]() будемо вважати відомою і неперервною.
Перетнемо тіло площинами, перпендикулярними
до осі
будемо вважати відомою і неперервною.
Перетнемо тіло площинами, перпендикулярними
до осі![]() ,
на відрізку
,
на відрізку![]() його довжини. В результаті наше тіло
розіб‘ється на
його довжини. В результаті наше тіло
розіб‘ється на![]() шарів, кожний з яких наближено можна
вважати за циліндр. Зважаючи на те, що
об‘ємі-го
шару наближено дорівнює
шарів, кожний з яких наближено можна
вважати за циліндр. Зважаючи на те, що
об‘ємі-го
шару наближено дорівнює
![]() ,
де
,
де![]() - деяка точка відрізка
- деяка точка відрізка![]() ,
то для об‘єму
,
то для об‘єму![]() усього тіла одержимо вираз
усього тіла одержимо вираз
|
|
(2.10) |
При
![]() та
та![]() наближена рівність (2.10) все точніше буде
характеризувати об‘єм тіла і у границі
одержимо
наближена рівність (2.10) все точніше буде
характеризувати об‘єм тіла і у границі
одержимо
![]() .
.
Оскільки
(2.10) являє собою інтегральну суму для
неперервної функції
![]() ,
то її границя є відповідний визначений
інтеграл. Отже,
,
то її границя є відповідний визначений
інтеграл. Отже,
|
|
(2.11) |
Приклад.
Знайти об‘єм
![]() піраміди, площа основи якої дорівнює
піраміди, площа основи якої дорівнює![]() ,
а висота
,
а висота![]() .
.

За вісь
![]() приймемо пряму, що виходить із вершини
піраміди, перпендикулярно її основі
(рис. 6).
приймемо пряму, що виходить із вершини
піраміди, перпендикулярно її основі
(рис. 6).
Позначимо
через
![]() площу якогось паралельного основі
перерізу на відстані
площу якогось паралельного основі
перерізу на відстані![]() від вершини. Відомо, що площі паралельних
перерізів піраміди відносяться як
квадрати їх відстаней від вершини. Отже,
від вершини. Відомо, що площі паралельних
перерізів піраміди відносяться як
квадрати їх відстаней від вершини. Отже,![]() .
Звідси
.
Звідси![]() і на основі (2.11)
і на основі (2.11)
![]() .
.
Отриманий результат повністю узгоджується із відомою формулою геометрії.
Об‘єм
тіла обертання. Нехай
криволінійна трапеція
![]() обертається
обертається

навколо
осі
![]() (рис. 7). Оскільки площа змінного поперечного
перерізу
(рис. 7). Оскільки площа змінного поперечного
перерізу![]() у точці
у точці![]() є круг радіуса
є круг радіуса![]() ,
то
,
то![]() .
Звідси на основі (2.11) одержимо
.
Звідси на основі (2.11) одержимо
|
|
(2.12) |
Якщо ж
криволінійна трапеція обмежена графіком
неперервної функції
![]() і прямими
і прямими![]() ;
;![]() ;
;![]() ,
тоді об‘єм тіла, утвореного обертанням
цієї трапеції навколо осі
,
тоді об‘єм тіла, утвореного обертанням
цієї трапеції навколо осі![]() визначається за формулою
визначається за формулою
|
|
(2.13) |
Приклад.
Визначити об‘єм тіла, утвореного
обертанням навколо осі
![]() кола
кола![]() .
.
Очевидно,
що обертання кола навколо осей
![]() або
або![]() утворює кулю, об‘єм якої
утворює кулю, об‘єм якої![]() .
Перевіримо це!
.
Перевіримо це!
Згідно з формулою (2.12) будемо мати
![]() .
.
Аналогічно,
при обертанні кола навколо осі
![]() одержимо, що
одержимо, що![]() .
.
Обчислення довжини дуги
Означення. Під довжиною дуги розуміють границю, до якої прямує довжина ламаної лінії, вписаної в цю дугу; коли число ланок зростає, а довжина найбільшої ланки прямує до нуля.
Нехай
на відрізку
![]() задана функція
задана функція![]() неперервна разом із своєю першою
похідною.
неперервна разом із своєю першою
похідною.
Довжина
дуги
![]() графіка цієї функції на відрізку
графіка цієї функції на відрізку![]() обчислюється за формулою
обчислюється за формулою
|
|
(2.14) |
де
![]() .
.
Приклад.
Обчислити довжину кола
![]() .
.
Для
застосування формули (2.14) потрібно
знайти похідну функції
![]() ,
заданої неявно. Похідна функції
,
заданої неявно. Похідна функції![]() знаходиться за формулою
знаходиться за формулою
![]() отже
отже
![]() ,
або
,
або![]() .
.
Тоді
![]()
![]() - довжина
півкола. Звідси довжина усього кола
- довжина
півкола. Звідси довжина усього кола
![]() .
.
