2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.

Нехай функція задана і неперервне на відрізкудеабо, а- деяка її первісна, тобтопри.

Теорема Якщо є якою-небудь первісною, то справедлива формула

,

(2.3)

тобто визначений інтеграл від від даної неперервної функції на даному відрізкудорівнює приросту її первісної

Ця формула називається формулою Ньютона-Лейбніца.

У виразі (2.3) числа іназиваються межами інтегрування, відповідно нижньою і верхньою,- проміжком інтегрування,- підінтегральною функцією. Формулу (2.3) можна подати як правило, а саме: визначений інтеграл дорівнює різниці значень первісної функції для верхньої і нижньої меж інтегрування. Запишемо це так:

(2.4)

де символ називається вставкою. Формула (2.4) дає практичне правило обчислення визначеного інтеграла. Воно означає знаходження невизначеного інтеграла, тобто первісної функціїіз наступним обчисленням її значень в точкахі.

Приклад. Обчислити інтеграл.

.

2.3. Основні властивості визначеного інтеграла.

При формулюванні основних властивостей визначеного інтеграла будемо виходити із формули (2.3), де - неперервна на відрізку, апри.

1. Величина визначеного інтеграла не залежить від позначення змінної інтегрування, тобто

2. Визначений інтеграл з однаковими межами інтегрування дорівнює нулю, тобто

.

3. При перестановці меж інтегрування визначений інтеграл змінює свій знак на протилежний, тобто

3. Якщо відрізок точкоюс поділений на два відрізкиі, то має місце рівність

3. Сталий множник виноситься за знак визначеного інтеграла, тобто

6. Визначений інтеграл від алгебраїчної суми скінченого числа неперервних функцій дорівнює такій же алгебраїчній сумі визначених інтегралів від цих функцій, тобто .

7. Якщо всюди на відрізку функція, то

8. Якщо всюди на відрізку виконується умова, то справедлива нерівність

.

9. Якщо функція 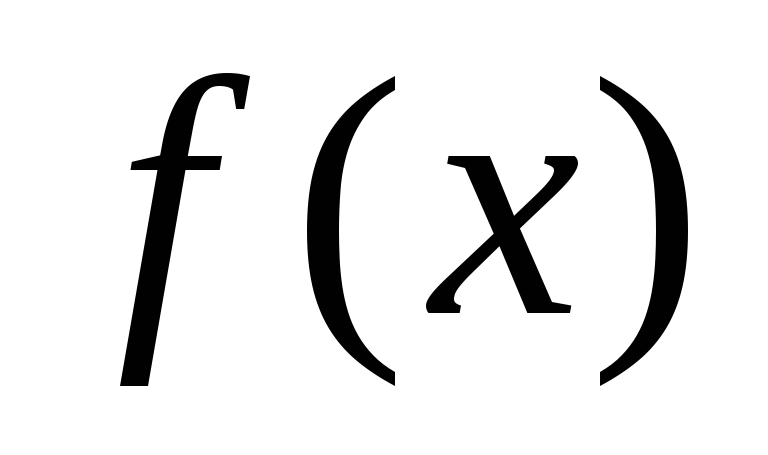інтегровна на відрізку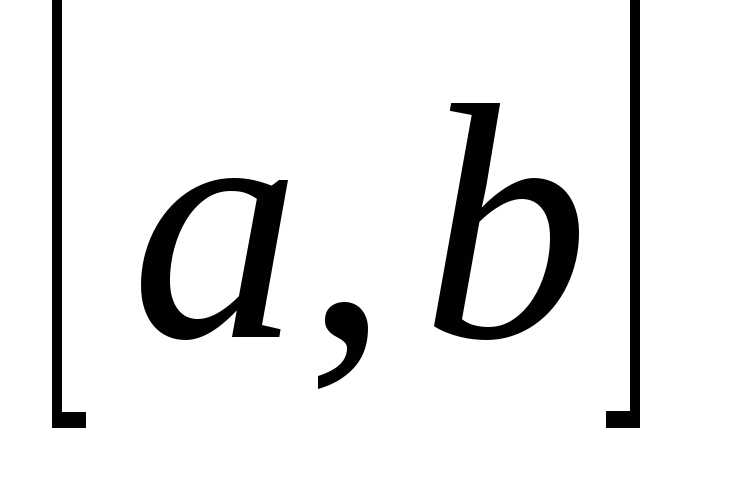, то

9. Якщо функція неперервна на відрізку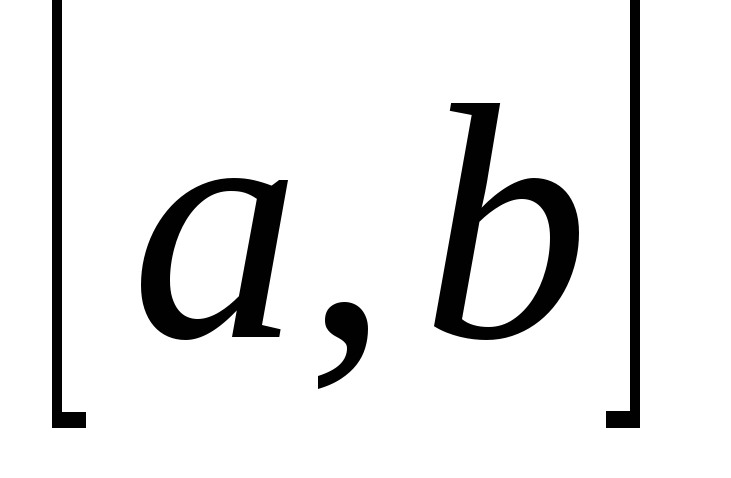, то на цьому відрізку знайдеться така точкас , що

11. Похідна визначеного інтеграла із змінною верхньою межою по цій межі дорівнює значенню підінтегральної функції для цієї межі, тобто

2.4. Методи обчислення визначених інтегралів

Обчислення визначених інтегралів здійснюється за формулами і правилами знаходження невизначених інтегралів із наступним використанням формули Ньютона-Лейбніца. Розглянемо деякі з них.

Інтегрування частинами у визначеному інтегралі.

Нехай функції інеперервно диференційовні на відрізку, тобтоі- неперервні функції. Тоді

або

Інтегруючи цю рівність в межах від до, одержимо

Звідси одержимо формулу інтегрування частинами

(2.5)

Приклад. Знайти інтеграл.

.

Заміна змінної у визначеному інтегралі.

Заміна змінної у визначеному інтегралі здійснюється як і у випадку невизначеного інтеграла з тим додатком, що із підстановки визначаються нові межі інтегрування. Старі і нові межі інтегрування зв’язані рівностями,. Формула (1.7) у даному випадку матиме вигляд

Приклад. Обчислити інтеграл.

=

;