
- •М.Д. Бабич, с.І. Куприков
- •1. Невизначений інтеграл
- •1.1. Первісна функція. Невизначений інтеграл.
- •1.2. Основні властивості невизначеного інтеграла
- •1.3. Таблиця основних невизначених інтегралів
- •Покажемо на прикладах, що наведені табличні інтеграли будуть вірні, коли - незалежній змінній і коли- диференційовній функції відx.
- •1.4. Основні методи інтегрування
- •1.5. Інтегрування раціональних дробів
- •1.6. Інтегрування простих ірраціональностей
- •1.7. Інтегрування тригонометричних функцій
- •1.8. Інтегрування деяких трансцендентних функцій
- •2. Визначений інтеграл
- •2.1. Визначений інтеграл як границя інтегральної суми
- •2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
- •2.3. Основні властивості визначеного інтеграла.
- •2.4. Методи обчислення визначених інтегралів
- •2.5. Застосування визначеного інтеграла
- •3. Функції двох змінних
- •3.1. Поняття функції двох змінних та їх геометричне зображення
- •3.2. Локальні екстремуми функції двох змінних
- •Дослідимо цю функцію всередині трикутника
- •4. Диференціальні рівняння
- •4.1. Основні поняття. Задача Коші.
- •4.2. Диференціальні рівняння першого порядку з відокремлюваними змінними
- •4.3. Лінійні диференціальні рівняння. Однорідні диференціальні рівняння
- •4.4. Диференціальні рівняння другого порядку
- •Диференціальні рівняння другого порядку, що допускають пониження порядку
- •4.5. Лінійні диференціальні рівняння другого порядку.
- •4.6. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.7. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •5. Числові та функціональні ряди
- •5.1. Числові ряди. Ознаки збіжності
- •5.2. Знакозмінні ряди
- •5.3. Функціональні ряди
- •5.4. Степеневі ряди. Радіус збіжності
- •5.5. Ряди Тейлора і Маклорена
- •Контрольна робота № 2
- •Рекомендована література
Контрольна робота № 2
Невизначений інтеграл. Визначений інтеграл та його застосування в геометрії. Частинні похідні та повний диференціал функції багатьох змінних. Диференціальні рівняння першого та другого порядків. Числові та степеневі ряди.
Знайти невизначені інтеграли
а)
 ;
;
б)
![]() ;
;
в)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
в)
![]() ;
;
3.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
4.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
5.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
г)
![]()
д)
![]() ;
;
е)
![]()
г)
![]() ;
;
д)
![]() ;
;
е)

г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]()
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
6.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
7.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
8.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
9.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
10.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
а)
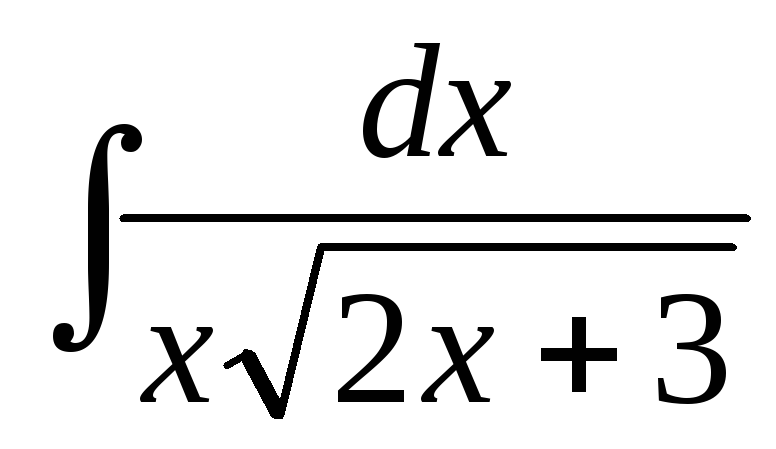 ;
;
б)
![]() ;
;
в)
![]() ;
;
а)
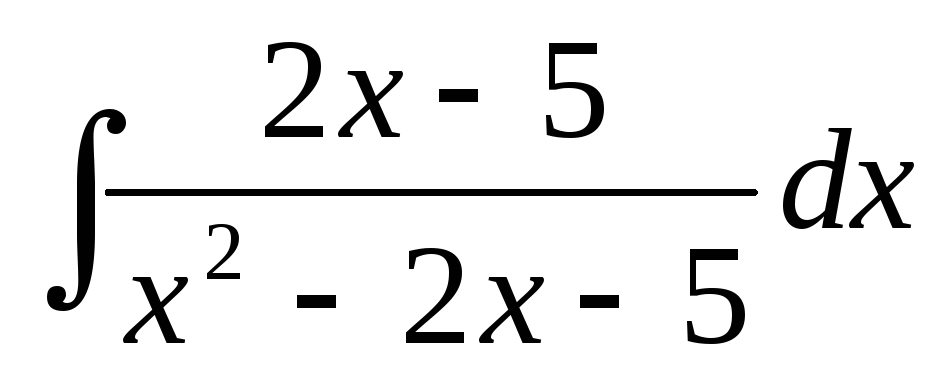 ;
;
б)
![]() ;
;
в)
![]() ;
;
13.а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)![]() ;
;
е)
![]() ;
;
а)
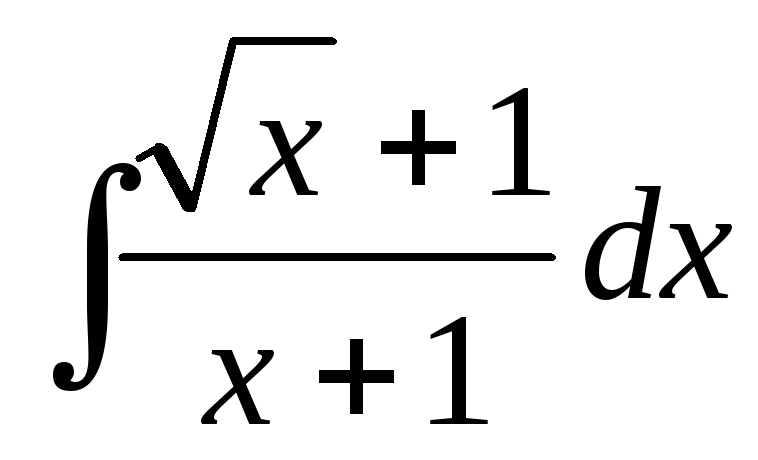 ;
;
б)
![]() ;
;
в)
![]() ;
;
15.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
16.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
17.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
18.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
19.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]()
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
20.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
21.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
22.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
23.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
24.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
25.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
26.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
в)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
в)
![]() ;
;
29.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
30.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ІІ. Обчислити визначений інтеграл.
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]() ;
;
11.
 ;
;
12.
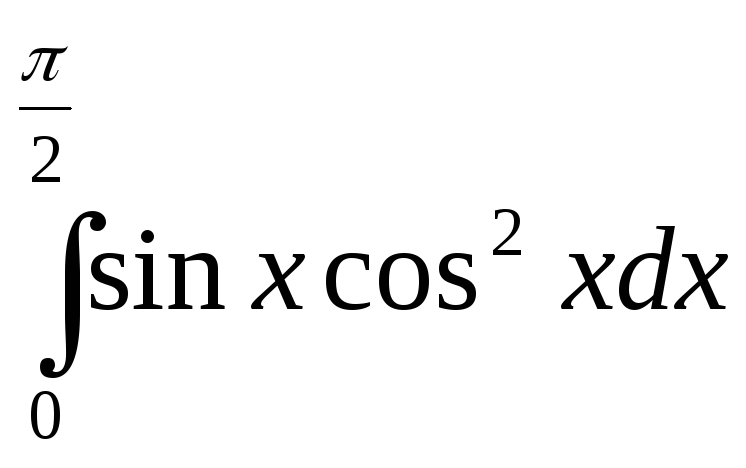 ;
;
13.
![]() ;
;
14.
![]() ;
;
15.![]() ;
;
16.
![]() ;
;
17.
 ;
;
18.
 ;
;
19.
![]() ;
;
20.
![]() ;
;
21.
 ;
;
22.
 ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]()
ІІІ. Застосування визначеного інтеграла в геометрії.
Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою .
.Обчислити площу фігури, обмеженої лініями
 ,
, ,
,
 іy=0.
іy=0. Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою .
.Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою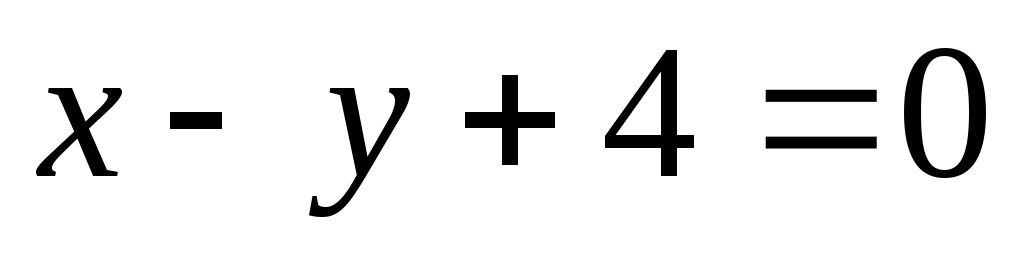 .
.Обчислити площу фігури, обмеженої параболою
 і віссю абсцисс.
і віссю абсцисс.Обчислити об’єм тіла, утвореного обертанням навколо осі ОХ фігури, яка обмежена гіперболою
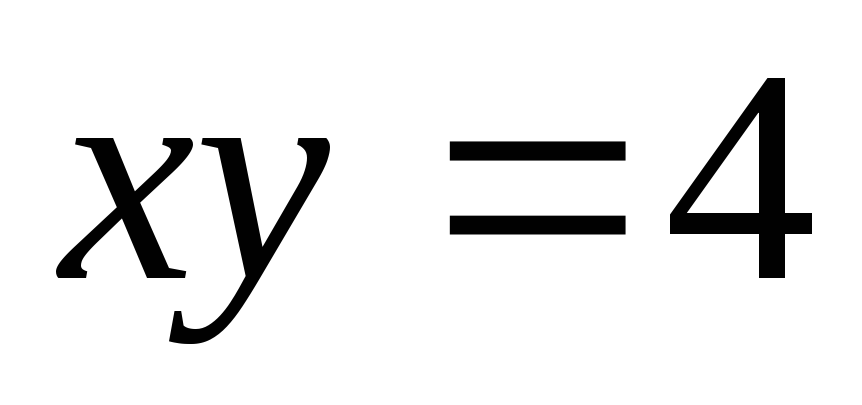 ,
прямимих=3,
х=12 та
віссю абсцисс.
,
прямимих=3,
х=12 та
віссю абсцисс.Обчислити об’єм тіла, утвореного обертанням навколо осі OY фігури, яка обмежена гіперболою
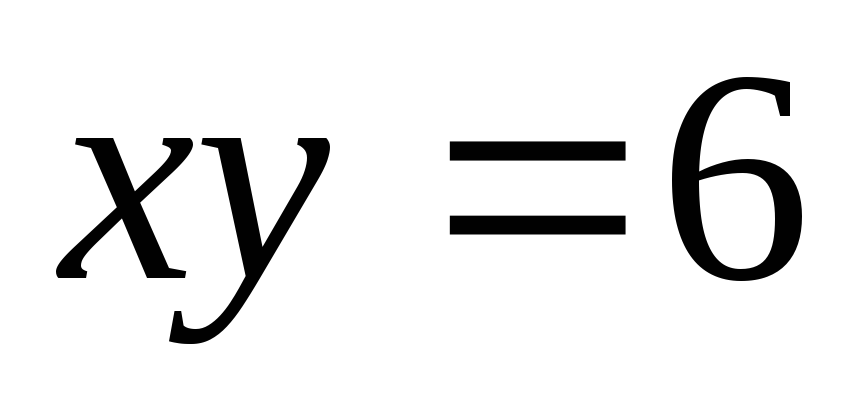 ,
прямими
,
прямими ,
, та віссюOY
.
та віссюOY
. Обчислити об’єм тіла, утвореного обертанням навколо осі OY фігури, яка обмежена параболою
 ,
прямою
,
прямою і віссюOY.
і віссюOY. Обчислити об’єм тіла, утвореного обертанням навколо осі ОХ фігури, яка обмежена параболою
 ,
прямою
,
прямою і віссюОХ.
і віссюОХ. Обчислити об’єм тіла, утвореного обертанням навколо осі ОХ фігури, яка обмежена лініями
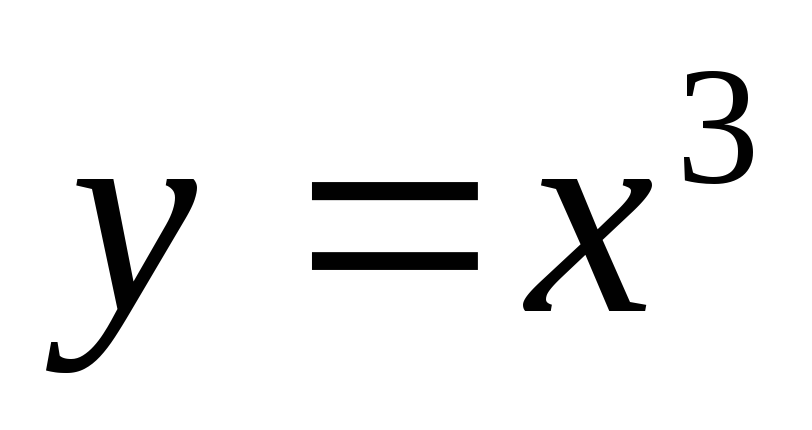 ,
, і
і .
.Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою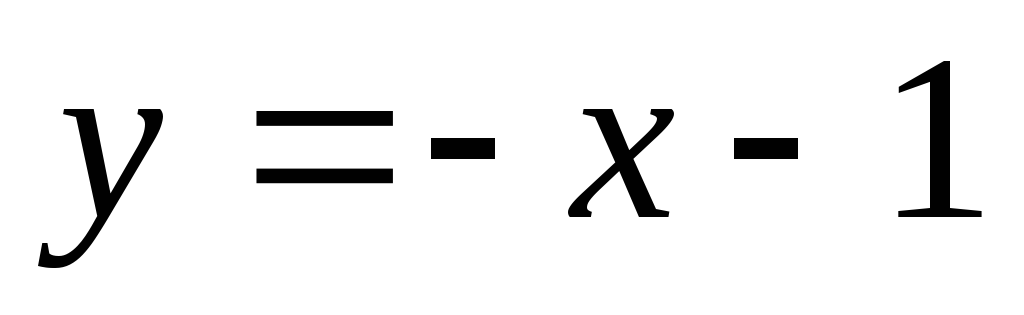 .
.Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою .
.Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою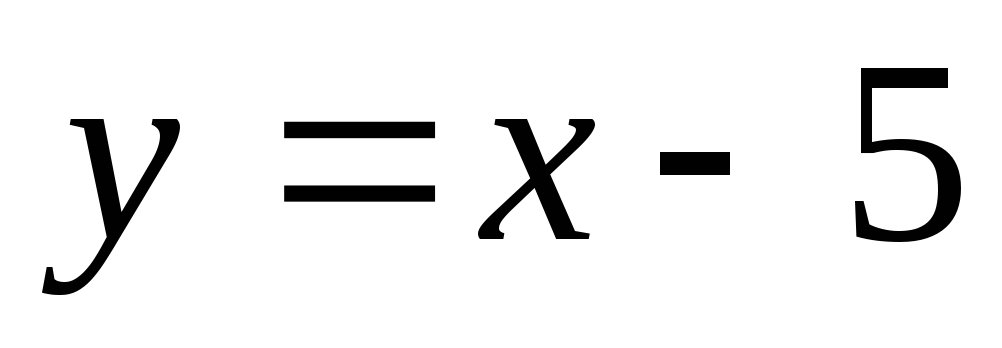 .
.
14.
Обчислити площу фігури, обмеженої
гіперболою
![]() ,
віссюОХ
і прямими х=2,
х=6.
,
віссюОХ
і прямими х=2,
х=6.
15.
Обчислити площу фігури, обмеженої
кривими
![]() і
і![]() .
.
Обчислити об’єм тіла, утвореного обертанням навколо осі ОY фігури, яка обмежена лініями
 ,
, і
і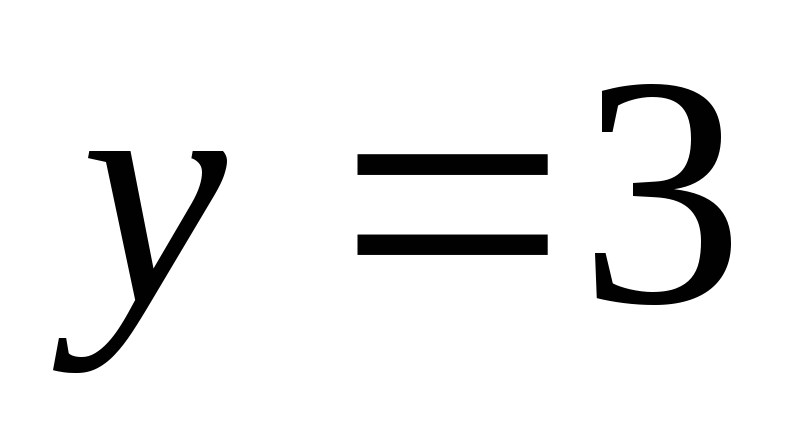 .
.Обчислити об’єм тіла, утвореного обертанням навколо осі ОХ фігури, яка обмежена лініями
 ,
, і
і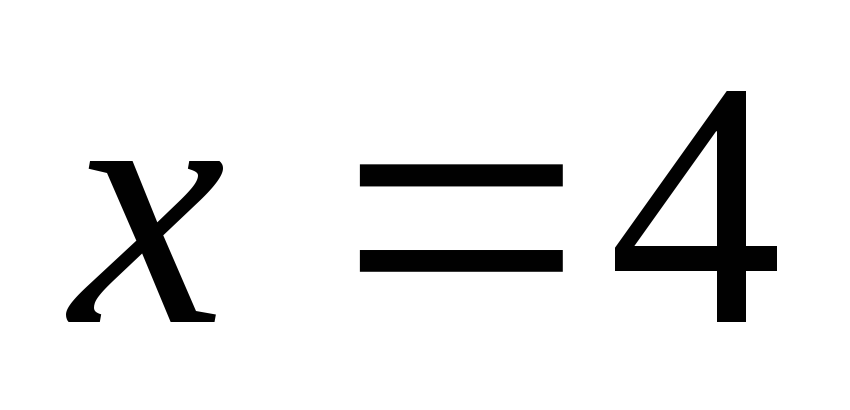 .
.Обчислити об’єм тіла, утвореного обертанням навколо осі ОY фігури, яка обмежена лініями
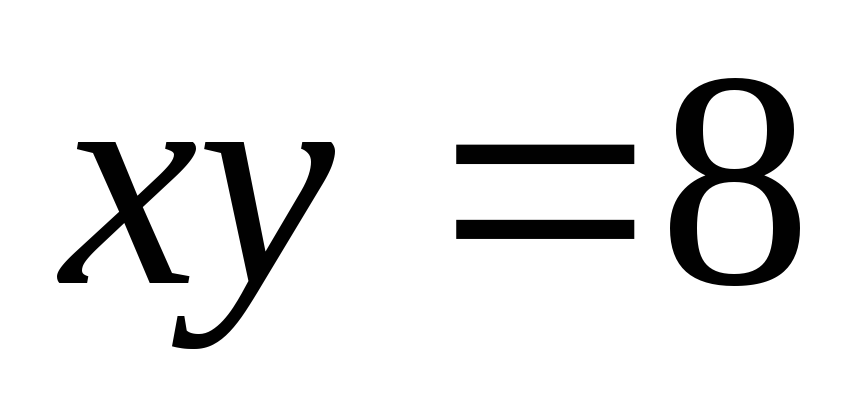 ,
, і
і ,
, .
.Обчислити об’єм тіла, утвореного обертанням навколо осі ОХ фігури, яка обмежена лініями
 ,
, і
і ,
, .
.Обчислити об’єм тіла, утвореного обертанням навколо осі ОY фігури, яка обмежена параболою
 ,
віссюОY
і прямою
,
віссюОY
і прямою
 .
.Обчислити площу фігури, обмеженої параболою
 і прямою
і прямою .
.Обчислити площу фігури, обмеженої лініями
 ,
, .
.Обчислити площу фігури, обмеженої кривими
 ,
, .
.
24.
Обчислити площу фігури, обмеженої
лініями
![]() ,
,![]() .
.
25.
Обчислити площу фігури, обмеженої
кривими
![]() ,
,![]() .
.
26.
Обчислити об’єм тіла, утвореного
обертанням навколо осі ОХ
фігури, яка обмежена
лініями
![]() ,
,![]() ,
,![]() .
.
27.
Обчислити об’єм тіла, утвореного
обертанням навколо осі ОY
фігури, яка обмежена
кривою
![]() ,
віссюОY
і прямою
,
віссюОY
і прямою
![]() .
.
28.
Обчислити об’єм тіла, утвореного
обертанням навколо осі ОХ
фігури, яка обмежена
кривою
![]() ,
віссюОХ
і прямими
,
віссюОХ
і прямими
![]() ,
,![]() .
.
Обчислити довжину дуги кривої
 від
від до
до .
.Обчислити площу фігури, обмеженої кривими
 ,
, .
.
IV. Знайти екстремум функції багатьох змінних
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
![]() ;
;
10.
![]()
11.
![]() ;
;
12.
![]() ;
;
13.
![]() ;
;
14.
![]() ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
![]() ;
;
18.
![]() ;
;
19.
![]() ;
;
20.
![]() ;
;
21.
![]() ;
;
22.
![]() ;
;
23.
![]() ;
;
24.
![]() ;
;
25.
![]() ;
;
26.
![]() ;
;
27.
![]() ;
;
28.
![]() ;
;
29.
![]() ;
;
30.
![]() ;
;
Знайти розв’язки диференціальних рівнянь.
а)
 ;
;
б)
![]() ;
;
2.
а)
![]() ;
;
б)
![]() ;
;
3.
а)
![]() ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
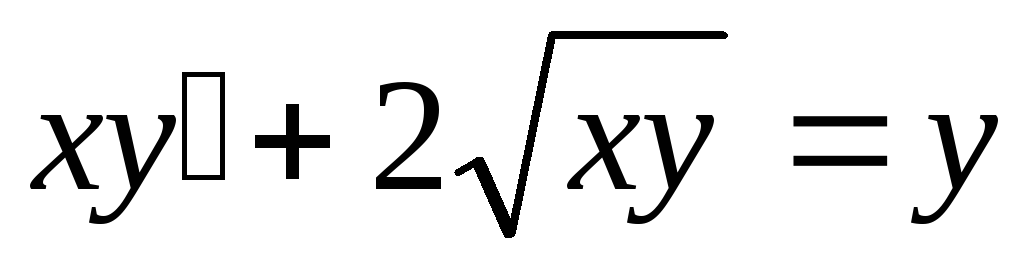 ;
;
б)
![]() ;
;
10.а)
![]() ;
;
б)
![]() ;
;
11.а)
![]() ;
;
б)
![]() ;
;
12.а)
![]() ;
;
б)
![]() ;
;
13.а)
![]() ;
;
б)
![]() ;
;
14.а)
![]() ;
;
б)
![]() ;
;
15.а)
![]() ;
;
б)
![]() ;
;
16.
а)
![]()
б)
![]()
17.а)
![]()
б)
![]()
18.
а)
![]()
б)
![]()
19.
а)
![]()
б)
![]()
20.
а)
![]()
б)
![]()
21.
а)
![]()
б)
![]()
22.
а)
![]()
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
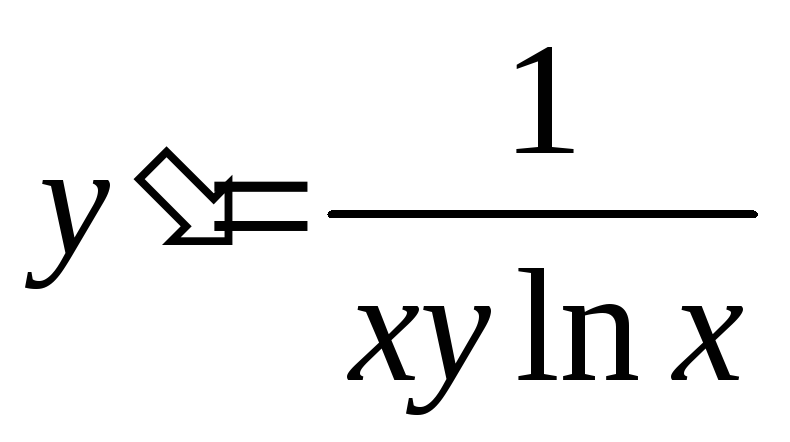 ;
;
б)
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
а)
 ;
;
б)
![]() ;
;
![]() ;
;
![]() .
.
VI. Числові та степеневі ряди.
а) Дослідити збіжність числового ряду.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
б) знайти інтервали збіжності степеневого ряду і дослідити його поведінку на кінцях інтервалу.
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
