5.4. Степеневі ряди. Радіус збіжності

Серед функціональних рядів степеневі ряди використовуються найбільш широко.

Означення. Степеневим рядом називається функціональний ряд виду

(5.5)

або, в загальному випадку

Числа називають коефіцієнтами степеневого ряду.

Теорема 1 (перша теорема Абеля). Якщо степеневий ряд збігається для значення, відмінного від нуля, то він абсолютно збігається для будь-якого значення, що задовільняє нерівності.

Якщо ж ряд розбігається при деякому значенні , то він розбігається при будь-якому, такому, що.

Теорема 2 (друга теорема Абеля – про будову області збіжності степеневого ряду). Для кожного степеневого ряду існує таке додатнє число(це може бути і), що

1. ряд збігається абсолютно для ,.

2. ряд розбігається для ,

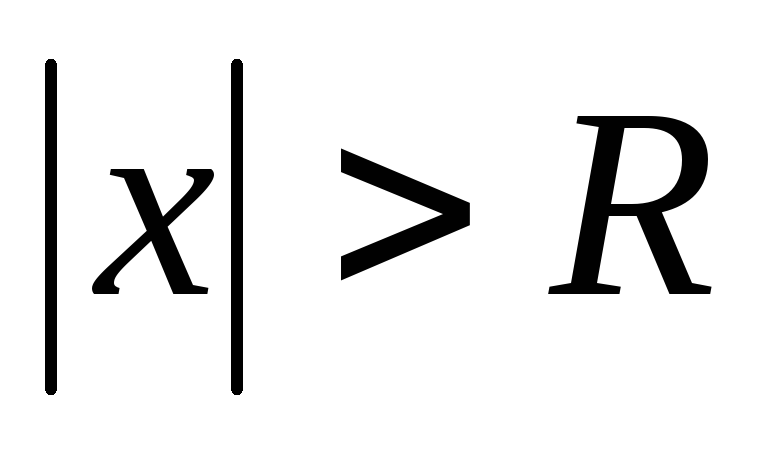
Число називається радіусом збіжності степеневого ряду.

Означення. Інтервалом збіжності степеневого ряду називається такий інтервал , що для будь-якого, що належить цьому інтервалові, ряд збігається, і притому абсолютно, а для всіх, що лежать зовні інтервала, ряд розбігається; значення,вимагають додаткової перевірки.

Теорема (про рівномірну збіжність степеневого ряду). Яке б додатнє число не взяти, степеневий ряд буде збігатися рівномірно відноснона відрізку.

Отже, в середині інтервалу збіжності степеневий ряд володіє всіма властивостями рівномірно збіжного функціонального ряду: його сума є неперервною функцією аргумента , його можна почленно інтегрувати та диференціювати.

Знаходження радіуса збіжності степеневого ряду

Для знаходження радіуса збіжності степеневого ряду поряд із рядом розглянемо ряд, утворений із абсолютних величин його членів:.

Для дослідження збіжності цього ряду (з додатними членами) скористуємось ознакою Даламбера

, .

Для збіжності ряду цей вираз повинен бути менше 1: , звідки; отже, інтервалі є інтервал збіжності степеневого ряду, тобто.

Якщо провести аналогічні міркування, користуючись ознакою Коші, то ми отримаємо: .

Приклад 1. Знайти інтервал збіжності степеневого ряду

(5.6)

Розв‘язання. Для знаходження інтервалу збіжності скористуємось ознакою Даламбера: ,;.

Отже, ряд збігається для значень , що задовольняють нерівності.

Дослідимо збіжність ряду на кінцях інтервалу. Для цього підставляємо значення ;в вираз (5.6).

При отримуємо ряд, який розбігається, як узагальнений гармонійний при.

При отримуємо ряд Лейбніца

,

який збігається умовно (за теоремою Лейбніца). Отже, інтервалом збіжності ряду (5.6) є .

Приклад 2. Знайти інтервал збіжності степеневого ряду .

Розв‘язання. Для знаходження інтервалу збіжності скористаємось ознакою Коші:

; ; таким чином, ряд збігається приі розбігається при.

Дослідимо збіжність на кінцях інтервалу:

при отримуємо гармонійний ряд, який є розбіжним;

при отримуємо знакочергуючий ряд, який за теоремою Лейбніца збігається умовно. Отже, інтервалом збіжності є.

5.5. Ряди Тейлора і Маклорена

Нехай функція на відрізкуабонескінчено диференційовна. Тоді для всіх значеньз цього проміжку має місце формула

(5.7)

Такий ряд (незалежно від того, чи є він збіжним і чи має своєю сумою функцію ) називається рядом Тейлора для функції.

Поклавши в цій формулі , отримаємо ряд Маклорена:

(5.8)

Як і для числових рядів, суму ряду Тейлора можна представити у вигляді часткової суми ряду і-го залишку ряду:.

Має місце наступна теорема:

Теорема (необхідні і достатні умови розвинення функції в ряд Тейлора). Для того, щоб ряд Тейлора збігався до функції , необхідно і достатньо, щоб призалишок ряду прямував до нуля:

для всіх значень із інтервалу збіжності ряду.

Розвинення в ряд Маклорена деяких функцій

1. ;

Запишемо ряд Маклорена:

Знайдемо коефіцієнти ряду для функції

.

. . . . . . . . . . . .

. . . . . .

Звідси маємо:

(Інтервал збіжності ряду ).

Замінивши в цій формулі на, отримуємо новий розклад:

2. :

;

Легко переконатись, що -на похідна може бути обчислена за формулою

.

Звідки маємо: ,.

Підставляючи ці значення в ряд Маклорена, отримуємо:

.

3. .

Міркуючи цілком аналогічно і зважуючи, що , отримаємо

; ,

Звідки

.

4. : Функція визначена і диференційовна при .

;

; ;;

; ... ; ;