
- •М.Д. Бабич, с.І. Куприков
- •1. Невизначений інтеграл
- •1.1. Первісна функція. Невизначений інтеграл.
- •1.2. Основні властивості невизначеного інтеграла
- •1.3. Таблиця основних невизначених інтегралів
- •Покажемо на прикладах, що наведені табличні інтеграли будуть вірні, коли - незалежній змінній і коли- диференційовній функції відx.
- •1.4. Основні методи інтегрування
- •1.5. Інтегрування раціональних дробів
- •1.6. Інтегрування простих ірраціональностей
- •1.7. Інтегрування тригонометричних функцій
- •1.8. Інтегрування деяких трансцендентних функцій
- •2. Визначений інтеграл
- •2.1. Визначений інтеграл як границя інтегральної суми
- •2.2. Обчислення визначеного інтеграла. Формула Ньютона-Лейбніца.
- •2.3. Основні властивості визначеного інтеграла.
- •2.4. Методи обчислення визначених інтегралів
- •2.5. Застосування визначеного інтеграла
- •3. Функції двох змінних
- •3.1. Поняття функції двох змінних та їх геометричне зображення
- •3.2. Локальні екстремуми функції двох змінних
- •Дослідимо цю функцію всередині трикутника
- •4. Диференціальні рівняння
- •4.1. Основні поняття. Задача Коші.
- •4.2. Диференціальні рівняння першого порядку з відокремлюваними змінними
- •4.3. Лінійні диференціальні рівняння. Однорідні диференціальні рівняння
- •4.4. Диференціальні рівняння другого порядку
- •Диференціальні рівняння другого порядку, що допускають пониження порядку
- •4.5. Лінійні диференціальні рівняння другого порядку.
- •4.6. Лінійні однорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •4.7. Лінійні неоднорідні диференціальні рівняння другого порядку із сталими коефіцієнтами
- •5. Числові та функціональні ряди
- •5.1. Числові ряди. Ознаки збіжності
- •5.2. Знакозмінні ряди
- •5.3. Функціональні ряди
- •5.4. Степеневі ряди. Радіус збіжності
- •5.5. Ряди Тейлора і Маклорена
- •Контрольна робота № 2
- •Рекомендована література
Диференціальні рівняння другого порядку, що допускають пониження порядку
Рівняння виду
 ,
що не містить шуканої функції та її
похідних.
,
що не містить шуканої функції та її
похідних.
Якщо
права частина рівняння залежить лише
від
![]() ,
то рівняння розв‘язується послідовним
інтегруванням. Дійсно, приймаючи до
уваги, що
,
то рівняння розв‘язується послідовним
інтегруванням. Дійсно, приймаючи до
уваги, що![]() ,
ми приходимо до рівняння
,
ми приходимо до рівняння
![]() або
або
![]() .
.
Інтегруючи праву та ліву частини, отримуємо
![]() .
.
Цілком
аналогічно, вважаючи, що
![]() і підставляючи замість
і підставляючи замість![]() його значення, будемо мати
його значення, будемо мати![]() .
.
Знов інтегруючи, отримаємо:
![]() .
.
Отже, загальний розв‘язок знаходиться шляхом двократного інтегрування (або, як кажуть, двократної квадратури).
Частинний
розв‘язок, що задовільняє початковим
умовам
![]() ,
,![]() знаходиться тим же шляхом, але враховуються
початкові умови:
знаходиться тим же шляхом, але враховуються
початкові умови:
Так, для
![]() отримаємо:
отримаємо: ,
,
а оскільки
![]() ,
то, підставляючи замість
,
то, підставляючи замість![]() значення
значення![]() ,
будемо мати
,
будемо мати
 ;
;
 .
.
Тоді
 .
.
Знов
покладаючи
![]() ,
отримаємо
,
отримаємо
![]() ,
звідки
,
звідки
 (оскільки
(оскільки
![]() є
стала).
є
стала).
Приклад.
Знайти частинний розв‘язок рівняння
![]() при заданих початкових умовах
при заданих початкових умовах![]() ;
;![]() .
.
![]() ;
;
![]()
Покладемо
тепер
![]() ;
тоді
;
тоді![]() .
.
![]() .
.
Інтегруємо другий раз:
![]() ;
;
![]()
![]()
![]() .
.
Поклавши
![]() і зважаючи, що
і зважаючи, що![]() ,
отримаємо, що
,
отримаємо, що![]() .
Звідси маємо частинний розв‘язок:
.
Звідси маємо частинний розв‘язок:
![]() або
або ![]() .
.
Рівняння виду
 ,
або
,
або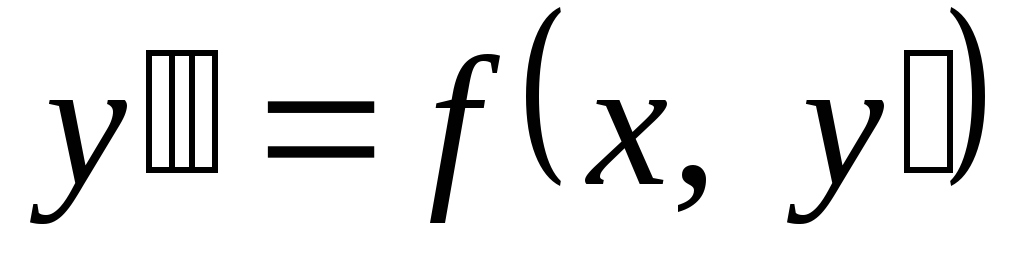 ,
що не містить явно шуканої функції
,
що не містить явно шуканої функції :
:
Таке
рівняння розв‘язується за допомогою
заміни
![]() ,
звідки
,
звідки![]()
![]() .
.
Підставивши ці значення у вихідне рівняння, ми отримуємо
![]()
а це вже
є рівняння першого порядку відносно
![]() .
Проінтегрувавши це рівняння, ми знайдемо
його загальний розв‘язок
.
Проінтегрувавши це рівняння, ми знайдемо
його загальний розв‘язок![]() ,
а потім із співвідношення
,
а потім із співвідношення![]() отримаємо загальний розв‘язок вихідного
рівняння
отримаємо загальний розв‘язок вихідного
рівняння
![]() .
.
Приклад.
![]() .
.
Робимо
заміну
![]() ;
підставляючи у вихідне рівняння,
отримуємо рівняння першого порядку:
;
підставляючи у вихідне рівняння,
отримуємо рівняння першого порядку:
![]() .
.
Відокремлюємо змінні
![]() .
.
![]() ;
;
![]() .
.
![]()
![]() .
Взявши тангенси від обох частин, отримаємо
.
Взявши тангенси від обох частин, отримаємо
![]() (за
формулою
(за
формулою
![]() ).
).
Повертаємось до вихідної змінної:
![]() ;
;
![]() ;
;![]() .
.
Обчислюємо цей інтеграл:
![]()
![]()
![]() ;
;
Звідси маємо загальний розв‘язок
![]()
Рівняння виду
 або
або ,
що
не містить явно незалежної змінної
,
що
не містить явно незалежної змінної
 :
:
Для
знаходження розв‘язку такого рівняння
знов використовується заміна
![]() ,
але тепер вважаємо
,
але тепер вважаємо![]() функцією
функцією![]() :
:![]() :
:![]() :
:![]() .
.
В
результаті відносно функції
![]() вихідне рівняння перетворюється в
рівняння першого порядку:
вихідне рівняння перетворюється в
рівняння першого порядку:
![]() .
.
Інтегруючи
це рівняння, знаходимо
![]() як функцію
як функцію![]() та довільної сталої
та довільної сталої![]() :
:
![]() ;
;
![]() .
.
Інтегруючи
останнє рівняння, отримуємо загальний
інтеграл вихідного рівняння:
![]() .
.
Приклад.
Знайти
розв‘язок рівняння
![]() ,
що задовольняє початковим умовам
,
що задовольняє початковим умовам
![]() ;
;
![]() .
.
Рівняння
не містить явно незалежної змінної
![]() ;
робимо заміну
;
робимо заміну![]() :
:
![]() .
.
Підставляємо ці значення у вихідне рівняння.
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
Підставляємо початкові умови:
![]() ;
;
![]() ,
звідки
,
звідки![]() ;
;![]() ;
;![]() .
.
Знов підставляємо початкові умови:
![]()
![]() .
.
Звідси отримуємо частинний розв‘язок:
![]() .
.
4.5. Лінійні диференціальні рівняння другого порядку.
Загальні поняття.
Лінійним диференціальним рівнянням другого порядку називається рівняння виду
![]() .
.
де
![]() та
та![]() - задані неперервні на інтервалі
- задані неперервні на інтервалі![]() функції. Якщо в цьому інтервалі функція
функції. Якщо в цьому інтервалі функція![]() ,
то рівняння називається однорідним,
якщо ж
,
то рівняння називається однорідним,
якщо ж![]() ,
то неоднорідним. Існування неперервних
на
,
то неоднорідним. Існування неперервних
на![]() функцій
функцій![]() та
та![]() забезпечує існування та єдиність
розв‘язку задачі Коші з довільними
початковими умовами при довільному
забезпечує існування та єдиність
розв‘язку задачі Коші з довільними
початковими умовами при довільному![]() .
.
Для однорідного рівняння мають місце наступні теореми:
Теорема
1. Якщо
![]() є частинний розв‘язок однорідного
лінійного диференціального рівняння
є частинний розв‘язок однорідного
лінійного диференціального рівняння
![]() ,
,
то
добуток
![]() ,
де
,
де![]() - довільна стала, також є розв‘язком
цього рівняння.
- довільна стала, також є розв‘язком
цього рівняння.
Теорема
2. Якщо
![]() та
та![]() є частинні розв‘язки однорідного
рівняння, то їх сума
є частинні розв‘язки однорідного
рівняння, то їх сума![]() також є розв‘язком цього рівняння.
також є розв‘язком цього рівняння.
Нагадаємо,
що функції
![]() називаються лінійно залежними на
називаються лінійно залежними на![]() якщо існують числа
якщо існують числа![]() ,
одночасно не рівні нулю, такі, що лінійна
комбінація
,
одночасно не рівні нулю, такі, що лінійна
комбінація
![]() .
.
Якщо ця
тотожність виконується лише в тому
випадку, коли всі
![]() ,
то функції
,
то функції![]() називаються лінійно незалежними.
називаються лінійно незалежними.
Якщо
функцій лише дві, то критерій лінійної
незалежності буде виконуватись, якщо
їх відношення
![]() .
Так, наприклад, функції
.
Так, наприклад, функції![]() і
і![]() є лінійно незалежними на будь-якому
інтервалі, оскільки
є лінійно незалежними на будь-якому
інтервалі, оскільки![]() .
.
Означення.
Система з двох лінійно незалежних на
інтервалі
![]() розв‘язків
розв‘язків![]() ,
,![]() однорідного лінійного диференціального
рівняння другого порядку з неперервними
на
однорідного лінійного диференціального
рівняння другого порядку з неперервними
на![]() коефіцієнтами називається фундаментальною
системою розв‘язків цього рівняння.
коефіцієнтами називається фундаментальною
системою розв‘язків цього рівняння.
Перевірити
лінійну незалежність розв‘язків можна
також за допомогою визначника Вронського.
Це визначник, складений з частинних
розв‘язків та їх похідних. Для рівняння
другого порядку він має такий вид
![]() .
.
Теорема.
Для того, щоб розв‘язки
![]() та
та![]() лінійного однорідного диференціального
рівняння були лінійно незалежними в
лінійного однорідного диференціального
рівняння були лінійно незалежними в![]() (в інтервалі неперервності коефіцієнтів
рівняння), необхідно і достатньо, щоб
(в інтервалі неперервності коефіцієнтів
рівняння), необхідно і достатньо, щоб![]() не обертався в нуль в жодній точці з
не обертався в нуль в жодній точці з![]() .
.
Теорема
(про структуру загального розв‘язку
однорідного лінійного диференціального
рівняння). Якщо функції
![]() та
та![]() утворюють фундаментальну систему
розв‘язків однорідного лінійного
диференціального рівняння другого
порядку з неперервними на
утворюють фундаментальну систему
розв‘язків однорідного лінійного
диференціального рівняння другого
порядку з неперервними на![]() коефіцієнтами, то загальний розв‘язок
рівняння має вигляд
коефіцієнтами, то загальний розв‘язок
рівняння має вигляд
![]() ,
де
,
де
![]() ,
а
,
а![]() - довільні сталі.
- довільні сталі.
Отже, щоб розв‘язати лінійне однорідне диференціальне рівняння другого порядку треба знайти його фундаментальну систему розв‘язків.
Можна показати, що інтегрування неоднорідного рівняння зводиться до інтегрування відповідного однорідного, якщо відомий частинний розв‘язок неоднорідного рівняння. Має місце наступна теорема.
Теорема(про структуру загального розв‘язку неоднорідного рівняня). Загальний розв‘язок лінійного неоднорідного диференціального рівняння дорівнює сумі довільного частинного розв‘язку цього рівняння і загального розв‘язку відповідного однорідного рівняння.
