
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Завдання для самостійної роботи
1. Знайти повний диференціал функцій:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
2.
Обчислити наближено
![]() .
.
3.
Знайти
![]() ,
якщо
,
якщо
![]() ,
,![]() ,
,![]() .
.
4.
Знайти
![]() ,
якщо
,
якщо
 ,
,![]() .
.
5.
Знайти
![]() і
і![]() ,
якщо
,
якщо
![]() ,
,![]() ,
,![]() .
.
2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
Якщо
задано функцію
![]() і обчислені її частинні похідні
і обчислені її частинні похідні![]() і
і![]() ,
то вони також є функціями незалежних
змінних
,
то вони також є функціями незалежних
змінних![]() і
і![]() ,
а тому від кожної із них можна обчислити
похідні як по змінній
,
а тому від кожної із них можна обчислити
похідні як по змінній![]() так і по змінній
так і по змінній![]() .
.
Частинні похідні від частинних похідних першого порядку називаються частинними похідними другого порядку. Вони позначаються:
 ,
,
 ,
,
 ,
,
 .
.
Аналогічно означаються і позначаються частинні похідні вищих порядків.
Частинні
похідні, які відмінні одна від одної
лише порядком диференціювання,
називаються мішаними
похідними.
Вони є рівними між собою при умові їх
неперервності, тобто
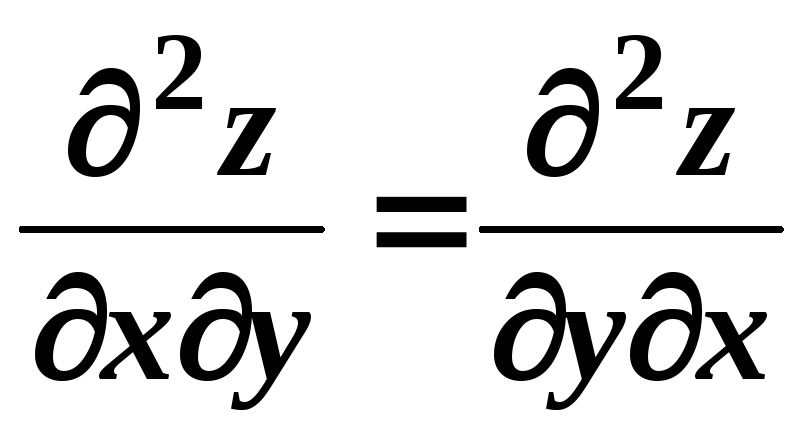 .
.
Похідна
від неявної функції,
яку задано рівнянням
![]() може бути обчислена за формулою:
може бути обчислена за формулою:
 .
(2.7)
.
(2.7)
Частинні
похідні неявної функції
![]() ,
заданої рівнянням
,
заданої рівнянням![]() ,
можуть бути обчисленні за формулами:
,
можуть бути обчисленні за формулами:
 ,
,
 .(2.8)
.(2.8)
Зразки розв’язування задач
1. Знайти частинні похідні другого порядку:
а)
![]() .
.
Знайдемо перші похідні:
![]() ,
,
![]() .
.
Знайдемо другі похідні:
 ,
,
 ,
,
 ,
,
 .
.
б)
![]() .
.
![]() ,
,
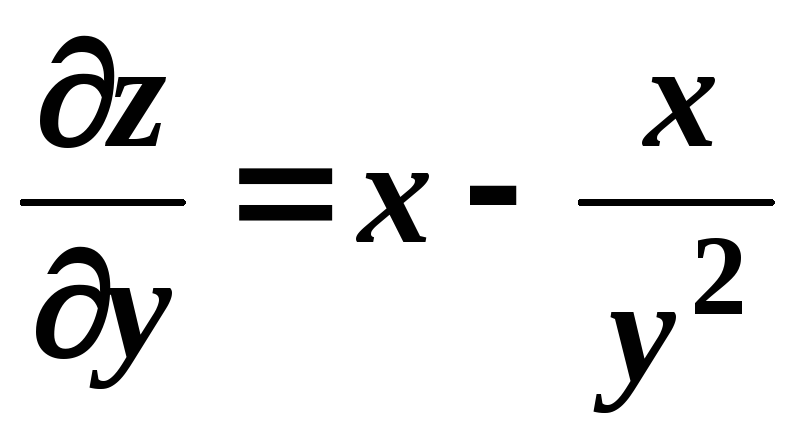 ;
;
 ,
,
 ,
,
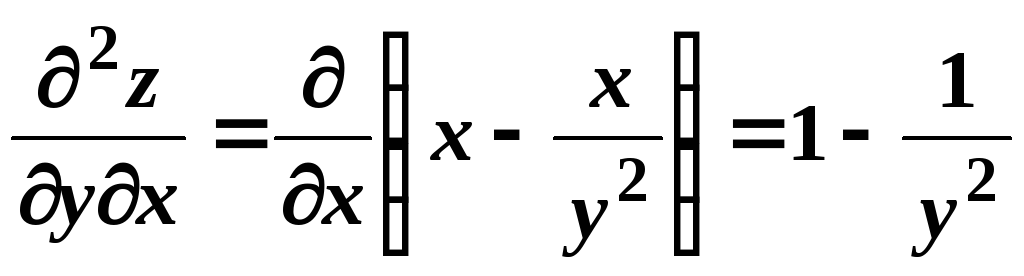 ,
,
 .
.
в)
![]() .
.
 ,
,
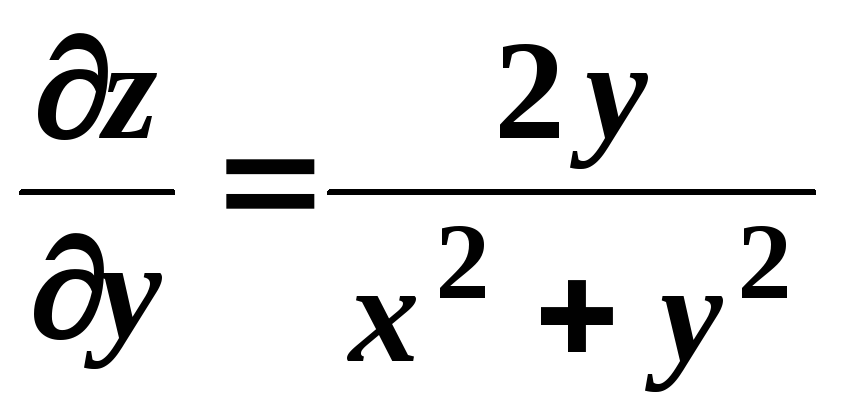 ;
;
 ,
,
 ,
,
 .
.
2.
Перевірити, що
 для функції
для функції![]() .
.
Знаходимо перші похідні:
 ,
,
 .
.
Обчислимо мішані похідні другого порядку:
 ,
,
 .
.
Як
бачимо,
 .
.
3.
Перевірити, що функція
![]() задовольняє рівняння
задовольняє рівняння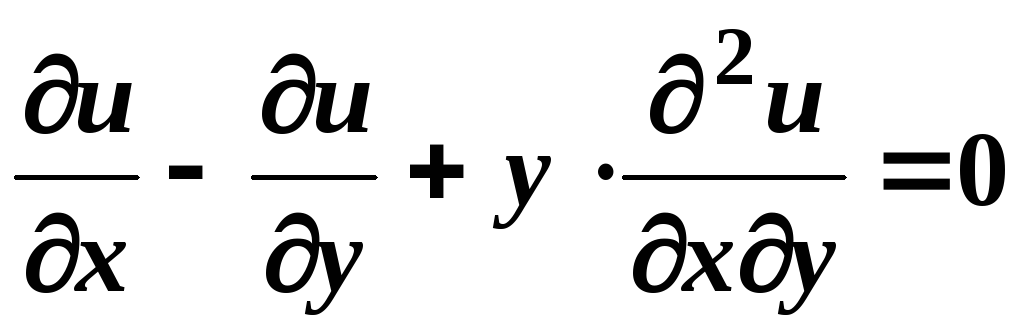 .
.
Знайдемо частинні похідні першого та другого порядку, які є в даному рівнянні:
 ,
,
 ;
;
 .
.
Підставляємо знайдені похідні в наше рівняння:
 або
або
 .
.
Отримаємо:
 ,
а саме
,
а саме![]() .
.
Ми
отримали тотожність, тому функція
![]() задовольняє дане рівняння.
задовольняє дане рівняння.
4.
Знайти похідну
![]() від функцій, заданих неявно:
від функцій, заданих неявно:
а)
![]() .
.
![]() .
.
Знайдемо
частинні похідні:
![]() ,
,![]() .
.
За
формулою (2.7) маємо:
 .
.
б)
![]() .
.
![]() .
.
![]() ,
,
 .
.
За
формулою (2.7) маємо:
 .
.
в)
![]() .
.
![]() .
.
Тоді
![]() ,
,![]() .
.
Отримаємо:
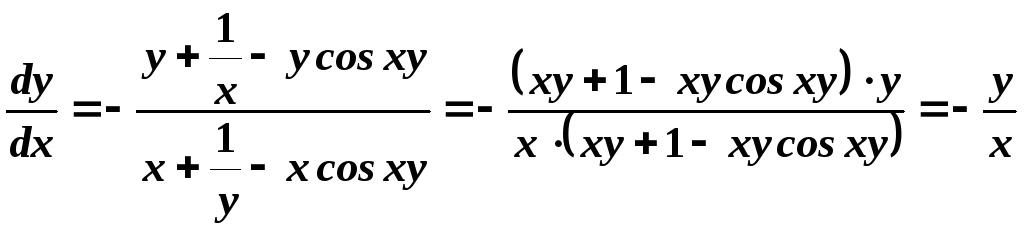 .
.
5.
Знайти
![]() та
та![]() від неявно заданих функцій:
від неявно заданих функцій:
а)
![]() .
.
![]() .
.
Обчислимо
![]() ,
,![]() ,
,![]() .
.
Зауважимо,
що
у
кожному
випадку
беручи
похідну
по
одній змінній, дві другі
вважаються
сталими.
За формулами
(2.8) маємо:
![]() ,
,![]() .
.
б)
![]() .
.
![]() .
.
Обчислимо
![]() ,
,![]() ,
,![]() .
.
Тоді
будемо мати:
![]() ,
,
 .
.
6.
![]() .
Знайти
.
Знайти![]() та
та![]() у точці
у точці![]() .
.
![]() .
.
Знайдемо
![]() ,
,![]() ,
,![]() .
.
За формулами (2.8):
![]() ,
тоді
,
тоді
![]() .
.
![]() ,
тоді
,
тоді
![]() .
.
Завдання для самостійної роботи
1. Знайти частинні похідні другого порядку:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
2.
Показати, що функція
![]() задовольняє рівняння
задовольняє рівняння .
.
3.
![]() .
Знайти
.
Знайти![]() ,
,![]() .
.
4.
Знайти
![]() від функцій, заданих неявно:
від функцій, заданих неявно:
а)
![]() ;
б)
;
б)![]() .
.
5.
Знайти
![]() та
та![]() ,
якщо
,
якщо![]() .
.
