
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Завдання для самостійної роботи
1. Знайти область визначення функцій:
а)
![]() ;
б)
;
б) ;
в)
;
в)![]() ;
г)
;
г) .
.
2. Знайти частинні похідні функцій:
а)
![]() ;
;
б)
![]() ;
;
в)
 ;
;
г)
![]() ;
;
д)
![]() ;
;
є)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
3.
Довести, що функція
![]() задовольняє рівняння
задовольняє рівняння
![]() .
.
2.2. Повний диференціал функції. Похідні складених функцій
Повний
приріст функції
![]() визначається за формулою
визначається за формулою
![]() ,
(2.1)
,
(2.1)
де
![]() і
і![]() - прирости незалежних змінних.
- прирости незалежних змінних.
Повним
диференціалом функції
![]() називається головна лінійна відносно
називається головна лінійна відносно![]() і
і![]() частина приросту функції, яка обчислюється
за формулою
частина приросту функції, яка обчислюється
за формулою
![]() ,
(2.2)
,
(2.2)
де
![]() ,
,![]() .
.
Для наближеного обчислення значення функції двох змінних користуються наближеною рівністю
![]() .
(2.3)
.
(2.3)
Ця
наближена рівність
тим
точніша, чим менше величини
![]() і
і![]() .
.
Нехай
![]() - функція двох змінних
- функція двох змінних![]() і
і![]() ,
кожна з яких, в свою чергу, є функцією
незалежної змінної
,
кожна з яких, в свою чергу, є функцією
незалежної змінної![]() :
:![]() ,
,![]() .
Тоді функція
.
Тоді функція![]() єскладеною
функцією змінної
єскладеною
функцією змінної
![]() .
.
Похідну цієї функції знаходять за формулою
![]() .
(2.4)
.
(2.4)
Зокрема,
якщо
![]() , а
, а![]() ,
то
,
то
![]() .
(2.5)
.
(2.5)
Нехай
![]() - функція двох змінних
- функція двох змінних![]() та
та![]() ,
які також залежать від змінних
,
які також залежать від змінних![]() та
та![]() :
:![]() ,
,![]() .
Тоді функція
.
Тоді функція![]() єскладеною
функцією незалежних змінних
єскладеною
функцією незалежних змінних
![]() та
та
![]() ,
а її частинні похідні по цим змінним
обчислюються за формулами:
,
а її частинні похідні по цим змінним
обчислюються за формулами:
(2.6) Зразки розв’язування задач
1. Знайти повний диференціал функцій:
а)
![]() .
.
Знайдемо частинні похідні:
![]() ;
;
 .
.
За формулою (2.2) будемо мати:
 .
.
б)
![]() .
.
![]() ;
;
![]() .
.
Отже,
![]() .
.
в)
![]() .
.
![]() ;
;
 .
Будемо мати:
.
Будемо мати: .
.
г)
![]() .
.
 ;
;
 .
.
Тоді отримаємо:
![]() .
.
2.
Обчислити наближено за допомогою
повного диференціала:
![]() .
.
Розглянемо
функцію
![]() ,
тоді
,
тоді![]() ;
;![]() .
Покладемо, що
.
Покладемо, що![]() ,
,![]() ,
обчислимо
,
обчислимо![]() ,
,![]() .
Тоді
.
Тоді![]() .
Знаходимо частинні похідні і їх значення
в точці
.
Знаходимо частинні похідні і їх значення
в точці![]() ,
а саме
,
а саме
 ,
тоді
,
тоді
 ;
;
 ,
тоді
,
тоді
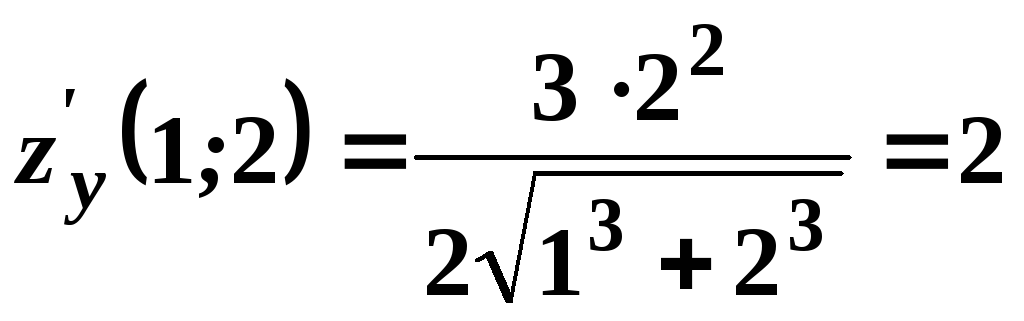 .
.
Повний диференціал
![]() .
.
Користуючись
формулою (2.3), отримаємо:
![]() ,
а саме:
,
а саме:![]() .
.
3.
Знайти
![]() ,
якщо
,
якщо![]() ,
,![]() ,
,![]() .
.
Функція
![]() є складеною функцією змінної
є складеною функцією змінної![]() ,
тому за формулою (2.4) отримаємо:
,
тому за формулою (2.4) отримаємо:![]() .
.
Будемо
мати:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Тоді шукана похідна запишеться у вигляді:
![]() .
.
Підставляючи
замість
![]() і
і![]() їхні вирази через
їхні вирази через![]() ,
дістанемо:
,
дістанемо:
![]() .
.
4.
Знайти
![]() ,
якщо
,
якщо![]() ,
,![]() ,
,![]() .
.
Функція
![]() є складеною функцією змінної
є складеною функцією змінної![]() ,
тому її похідна обчислюватиметься за
формулою (2.4):
,
тому її похідна обчислюватиметься за
формулою (2.4):
![]() .
.
Будемо
мати:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Тоді
![]()
![]() .
.
5.
Знайти
![]() ,
якщо
,
якщо![]() ,
,![]() .
.
Згідно
з формулою (2.5):
![]() .
Обчислимо:
.
Обчислимо:
 ,
,
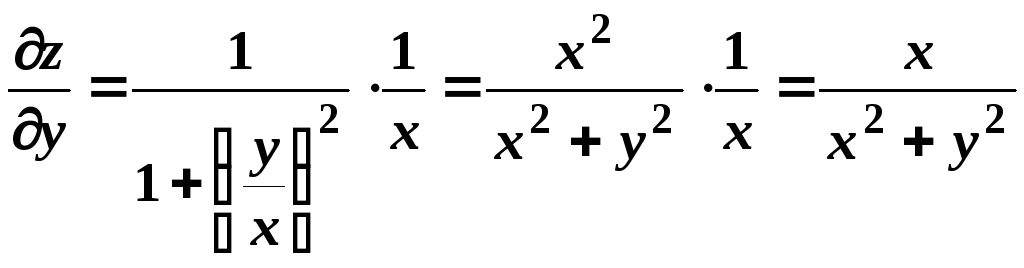 ,
,
 .
.
Тоді
 .
.
Підставляючи
замість
![]() його значення через
його значення через![]() ,
дістанемо:
,
дістанемо:

 .
.
6.
Знайти
![]() і
і![]() ,
якщо
,
якщо![]() ,
,![]() ,
,![]() .
.
Функція
![]() є складеною функцією змінних
є складеною функцією змінних![]() та
та![]() .
Для обчислення її похідних застосуємо
формули (2.6).
.
Для обчислення її похідних застосуємо
формули (2.6).
Будемо
мати:
![]() ,
,![]() .
.
Знайдемо
частинні похідні:
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
Підставляючи, отримаємо:
![]() ,
,
![]() .
.
Замінюючи
![]() і
і![]() виразами через
виразами через![]() і
і![]() ,
остаточно дістанемо:
,
остаточно дістанемо:
![]()
![]() ,
,
![]()
![]() .
.
7.
Знайти
![]() і
і![]() ,
якщо
,
якщо![]() ,
,![]() ,
,![]() .
.
Як
і в попередньому прикладі
![]() - складена функція змінних
- складена функція змінних![]() та
та![]() .
Обчислимо:
.
Обчислимо:![]() ,
, ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
За формулами (2.6) маємо:

![]() ,
,
 .
.
