
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Завдання для самостійної роботи
Дослідити функції та побудувати їхні графіки:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
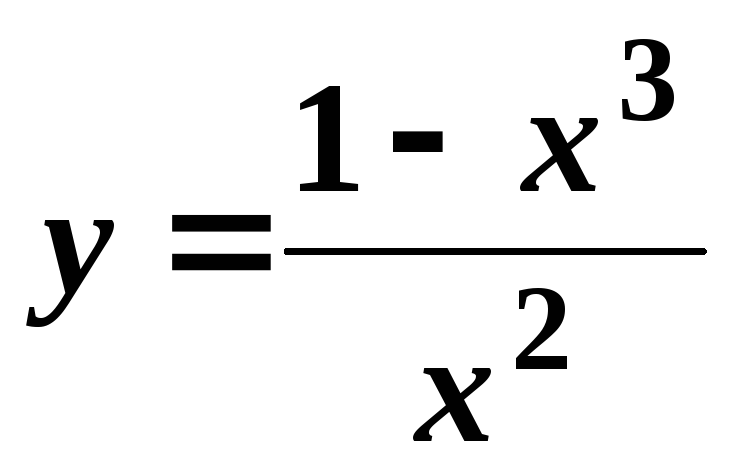 .
.
Розділ 2
ФУНКЦІЇ ДВОХ ЗМІННИХ
2.1. Означення та область визначення. Частинні похідні першого порядку
Нехай
![]() - множина упорядкованих пар чисел
- множина упорядкованих пар чисел![]() .
Якщо кожній парі чисел
.
Якщо кожній парі чисел![]() за певним законом відповідає число
за певним законом відповідає число![]() ,
то кажуть, що на множині
,
то кажуть, що на множині![]() визначено функцію
визначено функцію![]() від двох змінних
від двох змінних![]() і
і![]() і записують
і записують![]() .
.
Змінну
![]() називаютьзалежною
змінною (функцією),
а змінні
називаютьзалежною
змінною (функцією),
а змінні
![]() та
та![]() -незалежними
змінними (аргументами).
-незалежними
змінними (аргументами).
Множину
пар чисел
![]() ,
для яких функція
,
для яких функція![]() визначена, називаютьобластю
визначення функції
і позначають
визначена, називаютьобластю
визначення функції
і позначають
![]() .
Множину значень
.
Множину значень![]() позначають
позначають![]() .
.
Оскільки
кожній упорядкованій парі чисел
![]() відповідає в прямокутній системі
координат
відповідає в прямокутній системі
координат![]() єдина точка
єдина точка![]() площини, і, навпаки, кожній точці
площини, і, навпаки, кожній точці![]() площини відповідає єдина упорядкована
пара чисел
площини відповідає єдина упорядкована
пара чисел![]() ,
то функцію
,
то функцію![]() ,
де
,
де![]() ,
можна розглядати як функцію точки
,
можна розглядати як функцію точки![]() і замість
і замість![]() писати
писати![]() .
Областю визначення функції у цьому
випадку є деяка множина точок площини
.
Областю визначення функції у цьому
випадку є деяка множина точок площини![]() .
.
Значення
функції
![]() в точці
в точці![]() позначають
позначають![]() або
або![]() ,
або
,
або![]() .
.
Величина
![]() називаєтьсячастинним
приростом функції
називаєтьсячастинним
приростом функції
![]() по змінній
по змінній![]() .
.
Величина
![]() називаєтьсячастинним
приростом функції
називаєтьсячастинним
приростом функції
![]() по змінній
по змінній![]() .
.
Якщо
існує границя
![]() ,
то вона називаєтьсячастинною
похідною функції
,
то вона називаєтьсячастинною
похідною функції
![]() по змінній
по змінній![]() і позначається
і позначається
![]() .
.
Якщо
існує границя
 ,
то вона називаєтьсячастинною
похідною функції
,
то вона називаєтьсячастинною
похідною функції
![]() по змінній
по змінній![]() і позначається
і позначається
![]() .
.
При
обчисленні частинних похідних функції
двох
змінних користуються вже відомими
формулами і правилами диференціювання
функції однієї змінної. Слід лише
пам’ятати, що при знаходженні частинної
похідної
![]() обчислюють звичайну похідну функції
змінної
обчислюють звичайну похідну функції
змінної![]() ,
вважаючи змінну
,
вважаючи змінну![]() сталою. При знаходженні похідної
сталою. При знаходженні похідної![]() сталою вважається змінна
сталою вважається змінна![]() .
.
Зразки розв’язування задач
1. Знайти та зобразити області визначення функцій двох змінних:
а)
![]() .
.
Функція
не визначена лише тоді, коли
![]() .
Геометрично це означає, що область
визначення функції складається із двох
півплощин, одна з яких лежить вище, а
друга нижче прямої
.
Геометрично це означає, що область
визначення функції складається із двох
півплощин, одна з яких лежить вище, а
друга нижче прямої![]() (рис. 2.1)
(рис. 2.1)
б)
![]() .
.
Функція
визначена при умові
![]() ,
тобто
,
тобто![]() .
Рівняння
.
Рівняння![]() визначає в площині
визначає в площині![]() коло з центром в початку координат і
радіусом
коло з центром в початку координат і
радіусом![]() .
Функція визначена в точках, які лежать
усередині кола та на його межі, так як
для всіх точок, які лежать поза колом,
має місце нерівність
.
Функція визначена в точках, які лежать
усередині кола та на його межі, так як
для всіх точок, які лежать поза колом,
має місце нерівність![]() (рис.2.2).
(рис.2.2).


в)
![]() .
.
 Область
визначення цієї функції визначається
з нерівності
Область
визначення цієї функції визначається
з нерівності
![]() .
Межа області – парабола
.
Межа області – парабола![]() ,
яка ділить всю площину на дві частини.
Щоб виявити, яка з частин є областю
визначення даної функції, тобто
задовольняє умову
,
яка ділить всю площину на дві частини.
Щоб виявити, яка з частин є областю
визначення даної функції, тобто
задовольняє умову![]() ,
достатньо перевірити цю умову для
якої-небудь однієї точки, яка не лежить
на параболі. Наприклад, точка
,
достатньо перевірити цю умову для
якої-небудь однієї точки, яка не лежить
на параболі. Наприклад, точка![]() належить області визначення, тому що
належить області визначення, тому що![]() .
Отже, область визначення даної функції
є множина точок, розташованих нижче
параболи. Межа (парабола
.
Отже, область визначення даної функції
є множина точок, розташованих нижче
параболи. Межа (парабола![]() )
не належить до області визначення
функції. (рис. 2.3).
)
не належить до області визначення
функції. (рис. 2.3).
г)
z![]() .
.
Областю
визначення цієї функції є сукупність
пар
![]() і
і![]() ,
які задовольняють нерівностям
,
які задовольняють нерівностям![]() .
На площині
.
На площині![]() ця область є смуга, обмежена прямими
ця область є смуга, обмежена прямими![]() і
і![]() (рис.2.4)
(рис.2.4)

2. Знайти частинні похідні функцій:
а)
![]() .
.
Функція
![]() є функцією двох змінних
є функцією двох змінних![]() і
і![]() .
Припускаючи, що
.
Припускаючи, що![]() стала й обчислюючи похідну від функції
стала й обчислюючи похідну від функції![]() по
по![]() ,
знаходимо частинну похідну по
,
знаходимо частинну похідну по![]() :
:
![]() .
Припускаючи,
що стала
.
Припускаючи,
що стала
![]() й обчислюючи похідну від функції
й обчислюючи похідну від функції![]() по
по![]() ,
знаходимо частинну похідну по
,
знаходимо частинну похідну по![]() :
:
![]() .
.
б)
![]() .
.
Вважаючи,
що
![]() ,
маємо:
,
маємо:
![]() .
.
Якщо,
![]() ,
то
,
то
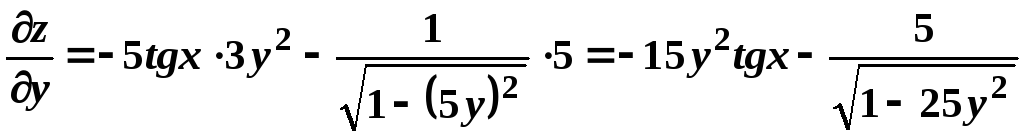 .
.
в)
![]() .
.
![]() ;
;
![]() .
.
г)
![]() .
.
![]() ;
;
 .
.
д)
![]() .
.
При
диференціюванні по
![]() функція має вигляд
функція має вигляд![]() .
Тому
.
Тому
 .
.
При
диференціюванні по
![]() функція набуває вигляду
функція набуває вигляду![]() ,
тому
,
тому
![]() .
.
є)
 .
.
Аналогічно попередньому прикладу маємо:
 ;
;

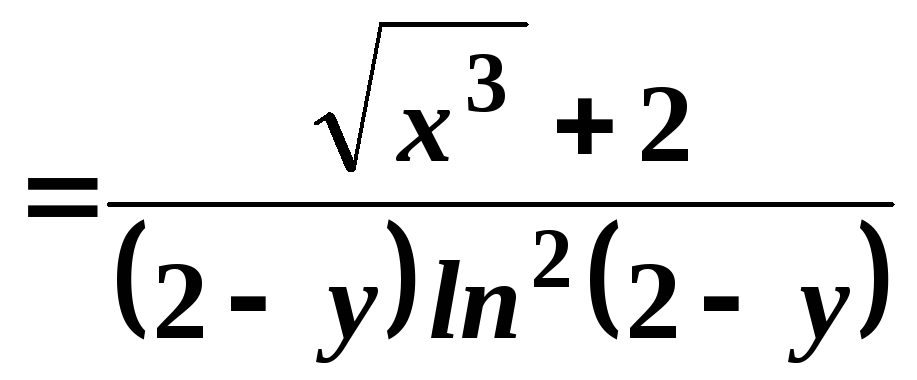 .
.
ж)
![]() .
.
При
знаходженні частинних похідних
![]() і
і![]() маємо функцію
маємо функцію![]() у вигляді дробу, в чисельнику і знаменнику
якого знаходяться змінні. Тому застосуємо
правило диференціювання частки двох
функцій, а саме:
у вигляді дробу, в чисельнику і знаменнику
якого знаходяться змінні. Тому застосуємо
правило диференціювання частки двох
функцій, а саме:
 ;
;
 .
.
з)
![]() .
.
При
диференціюванні по
![]() задану функцію треба розглядати як
степеневу
задану функцію треба розглядати як
степеневу![]() .
Тоді отримаємо
.
Тоді отримаємо![]() .
При диференціюванні по
.
При диференціюванні по![]() функція має вигляд показникової
функція має вигляд показникової![]() . Будемо мати
. Будемо мати![]() .
.
і)
![]() .
.
Аналогічно
попередньому прикладу маємо: по
![]() функція є показниковою, а по
функція є показниковою, а по![]() - степеневою. Знаходимо:
- степеневою. Знаходимо: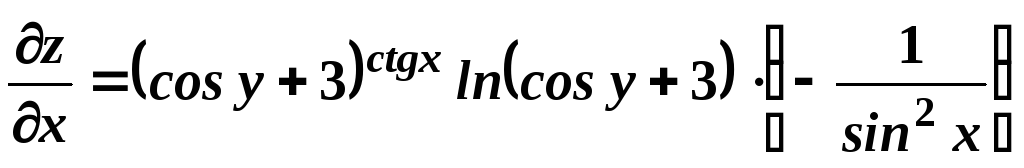 ;
;![]() .
.
к)
![]() .
.
Обчислюючи
![]() ,
вважаємо
,
вважаємо![]() і знаходимо частинну похідну від
складеної функції по
і знаходимо частинну похідну від
складеної функції по![]() :
: .
.
Обчислюючи
похідну
![]() ,
вважаємо
,
вважаємо![]() ,
а функцію
,
а функцію![]() - складеною по
- складеною по![]() :
: .
.
л)
![]() .
.
 ;
;
 .
.
м)
![]() .
.
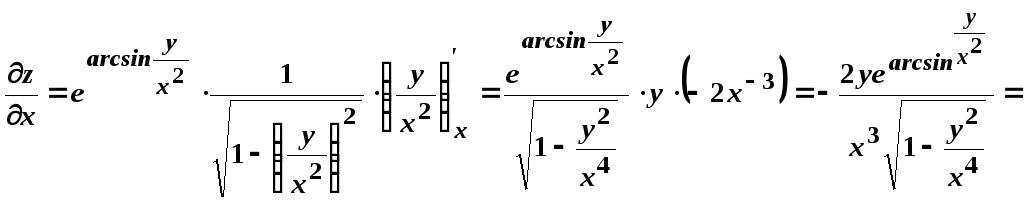
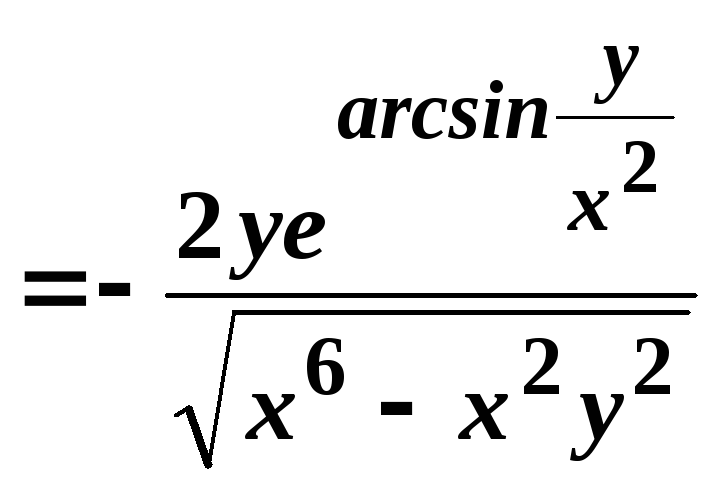 ;
;
 .
.
н)
![]() .
.
 ;
;
 .
.
3.
Довести, що функція
![]() задовольняє рівняння
задовольняє рівняння![]() .
.
Знайдемо
частинні похідні функції
![]() :
:
![]() ;
;
![]() .
.
Підставимо
саму функцію
![]() та її частинні похідні в наведене
рівняння:
та її частинні похідні в наведене
рівняння:
![]()
![]() .
.
Будемо мати:
![]() ;
;
![]() .
.
Отримано
тотожність, це означає, що функція
![]() задовольняє рівняння.
задовольняє рівняння.
