Завдання для самостійної роботи

Обчислити інтеграли:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. ;

14. ;

15. ;

16. .

3.6. Інтегрування деяких іраціональних функцій

Насамперед зауважимо, що інтеграл від іраціональної функції не завжди обчислюється в скінченному вигляді. Розглянемо деякі типи таких інтегралів, які за допомогою певної підстановки можна звести до інтеграла від раціональної функції, а отже, знайти його.

1) Інтеграли виду , де>,- натуральні числа, обчислюються за допомогою підстановки, де- спільний знаменник дробів.

2) Інтеграли виду ,

де - дійсні числа, причому(бо у противному випадку відношенняє сталим і підінтегральна функція в цьому разі є раціональною функцією від) за допомогою підстановкизводяться до інтегралів від раціональної функції змінної.

3) а) Інтеграли виду вилученням повного квадрату під радикалом зводяться до табличних інтегралів:

, ;

б) інтеграли виду за допомогою підстановкизводяться до інтегралів попереднього виду.

4) Для перелічених нижче видів іраціональностей використовуються тригонометричні підстановки, що дозволяють прийти до інтегралів від тригонометричних функцій і.

Розглянемо випадки:

а) для інтегралів виду застосовується підстановкаабо;

б) для інтегралів виду застосовується підстановкаабо;

в) для інтегралів виду підстановкаабодає змогу позбутися іраціональності.

Зразки розв’язування задач

Обчислити інтеграли.

1. .

Найменшим спільним кратним показників коренів є . Виконаємо підстановку, , , .

.

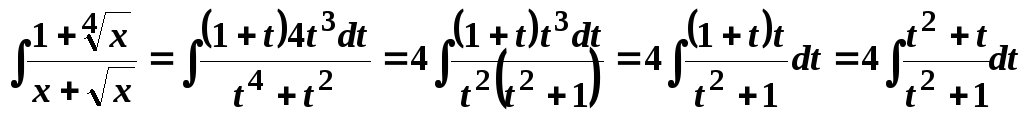Отримали інтеграл від неправильного раціонального дробу. Виділивши цілу частину дробу і виконавши почленне ділення в отриманому правильному дробу, матимемо:

.

Повернемось до початкової змінної, враховуючи що . Тоді.

2. .

Для інтегрування отриманого раціонального дробу запишемо його у вигляді суми найпростіших дробів:

.

Невизначені коефіцієнти знайдемо порівнянням коефіцієнтів при однакових степеняхв лівій та правій частинах рівності:.Отримаємо: .

Шуканий інтеграл матиме вигляд:

.

3.

.

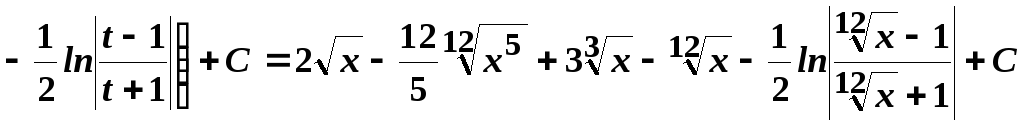4.

.

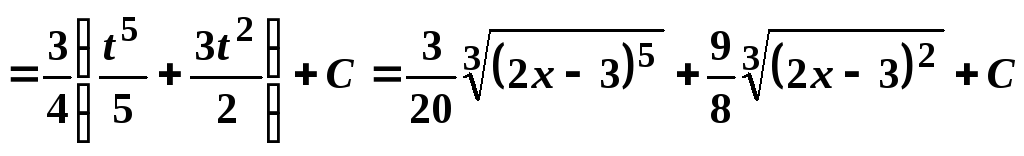5.

.

6.

.

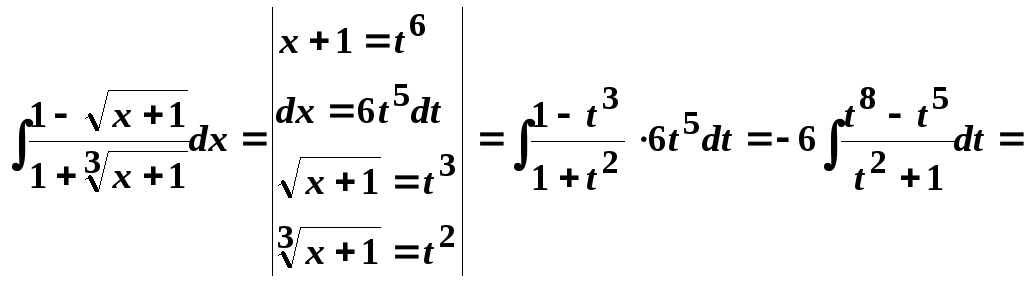
7. .

Введемо підстановку . Тоді, , , , звідки . Знайдемо: .

Після підстановки отримаємо: . Інтеграл може бути обчислений розкладанням дробу на суму найпростіших дробів. Розглянемо інший спосіб. Проінтегруємо частинами:

.

Повернувшись до початкової змінної, маємо:

.

8. .

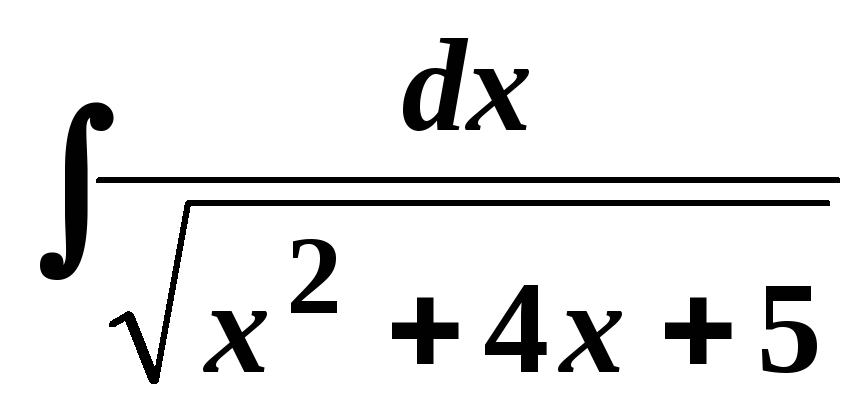Виділимо під коренем повний квадрат, звівши тим самим інтеграл до табличного:

.

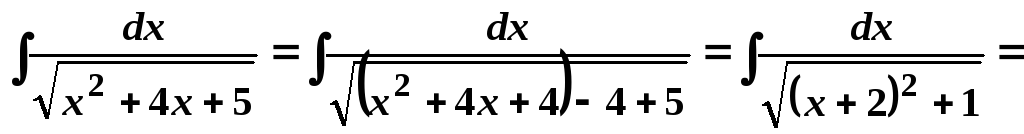
9. .

Перетворимо підкореневий вираз:

.

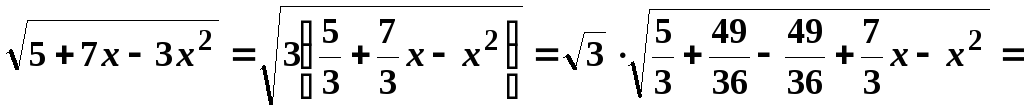
Тоді інтеграл має вигляд:

.

10. .

Використаємо підстановку ,.

.

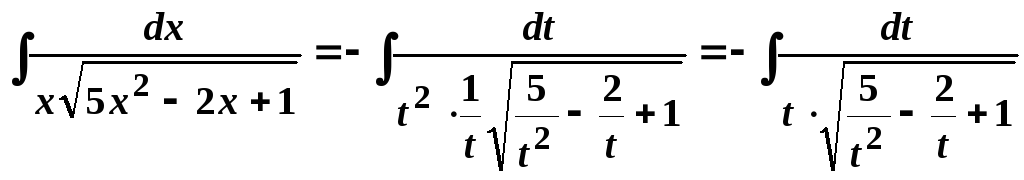Внесемо в знаменнику під корінь і отримаємо:

.

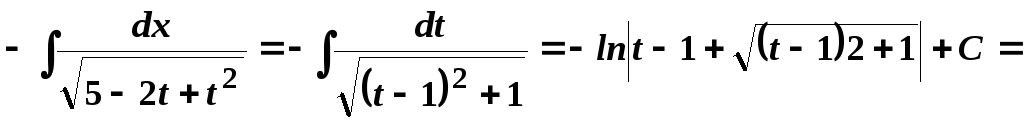
11. .

Обчислимо даний інтеграл за допомогою заміни . Тоді,,.

Маємо:.

Обчислимо отриманий інтеграл, використовуючи формулу пониження степеня:.

Отримаємо:

.

Зауваження. У перетвореннях використовуються тотожності:

, .

12.

.

Враховуючи, що , маємо далі:

.

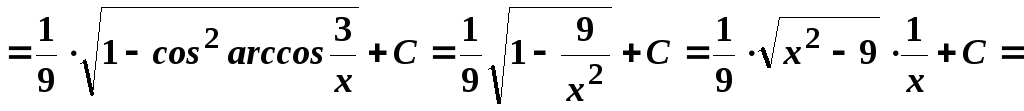
13.

.

Зауваження. У перетвореннях використовуються тотожності:

, .