
- •З м і с т
- •Розділ 1 застосування диференціального числення для дослідження функцій
- •1.1. Зростання і спадання функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.2. Локальний екстремум функції
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.3. Опуклість і угнутість кривих. Точки перегину
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.4. Асимптоти кривих
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •1.5. Схема дослідження функції та побудова її графіка
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 2
- •2.1. Означення та область визначення. Частинні похідні першого порядку
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.2. Повний диференціал функції. Похідні складених функцій
- •(2.6) Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.3. Частинні похідні вищих порядків. Похідні неявно заданих функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •2.4. Рівняння дотичної площини і нормалі до поверхні. Екстремум функції двох змінних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Розділ 3 невизначений інтеграл
- •3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
- •Таблиця основних інтегралів
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Зразки розв’язування задач
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.5. Інтегрування функцій, раціонально залежних від тригонометричних
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •3.6. Інтегрування деяких іраціональних функцій
- •Зразки розв’язування задач
- •Завдання для самостійної роботи
- •Вища математика
Розділ 3 невизначений інтеграл
3.1. Поняття первісної функції та невизначеного інтеграла. Метод безпосереднього інтегрування
Функція
![]() називаєтьсяпервісною
функції
називаєтьсяпервісною
функції
![]() на проміжку
на проміжку![]() ,
якщо
,
якщо![]() диференційовна на
диференційовна на![]() і
і![]() для всіх
для всіх![]() .
Очевидно, що будь-яка з функцій
.
Очевидно, що будь-яка з функцій![]() ,
де
,
де![]() - довільна стала, також є первісною
функції
- довільна стала, також є первісною
функції![]() на цьому проміжку.
на цьому проміжку.
Сукупність
усіх первісних функції
![]() на проміжку
на проміжку![]() називаютьневизначеним
інтегралом
функції
називаютьневизначеним
інтегралом
функції
![]() на цьому проміжку і позначають
на цьому проміжку і позначають
![]() ,
,
де
![]() - підінтегральна функція,
- підінтегральна функція,![]() - підінтегральний вираз,
- підінтегральний вираз,![]() - довільна стала.
- довільна стала.
Операцію знаходження невизначеного інтеграла від функції називають інтегруванням цієї функції.
Властивості невизначеного інтеграла:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
Якщо
![]() і
і![]() - довільна функція, що має неперервну
похідну, то
- довільна функція, що має неперервну
похідну, то![]() .
.
При
обчисленні невизначених інтегралів
зручно користуватися наступними
правилами: якщо
![]() ,
тоді
,
тоді
![]() ,
,
![]() ,
,
![]() ,
,
де
![]() та
та![]() - сталі величини.
- сталі величини.
Таблиця основних інтегралів
1.

![]() ,
,
1'.
![]() ,
,
2.
![]() ,
,
3.
 ,
,
![]() >
>![]() ,
,![]() ,
,
3'.
![]() ,
,
4.
![]() ,
,
5.
![]() ,
,
6.
![]() ,
,
7.
![]() ,
,
8.
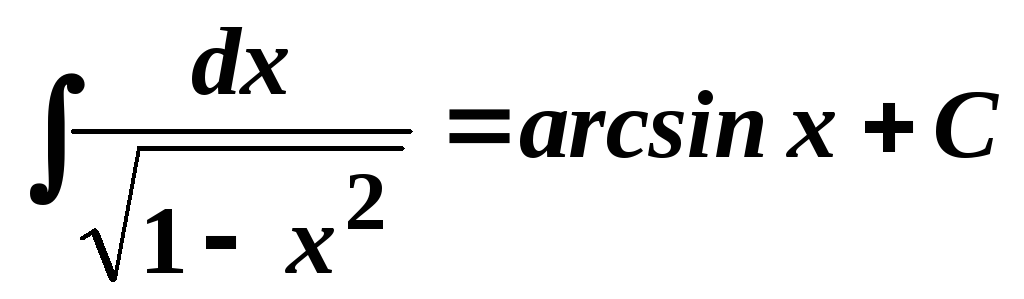 ,
,
8'.
 ,
,
![]() >
>![]() ,
,
9.
![]() ,
,
9'.
![]() ,
,
![]() ,
,
10.
 ,
,
![]() ,
,
11.
 ,
,
![]() ,
,
12.
![]() ,
,
13.
![]() ,
,
14.
![]() ,
,
15.
 .
.
Зауваження. Варто відзначити, що задача інтегрування функції вирішується неоднозначно. Тобто один і той же інтеграл може бути обчислений не єдиним методом.
Метод безпосереднього інтегрування полягає у зображенні вихідного інтеграла у вигляді алгебраїчної суми табличних інтегралів.
Зразки розв’язування задач
Обчислити інтеграли.
1.
![]() .
.
Користуючись властивостями 4 та 5, будемо мати:

2.

![]()
3.


4.


5.
 .
.
Тут, крім властивостей 4 та 5, застосуємо правила інтегрування. Дістанемо:

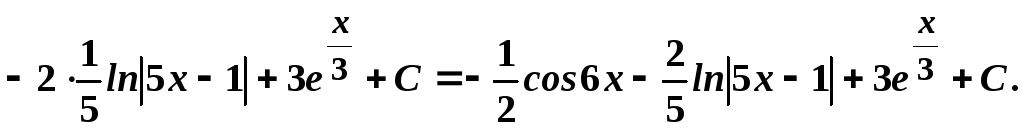
6.

![]()

7.
 .
.
Інтеграл
не є табличним, тому за допомогою
алгебраїчних перетворень треба
підінтегральну функцію подати у такому
вигляді, щоб можна було застосувати
властивості невизначеного інтеграла
та обчислити його. Для цього в чисельнику
дробу додамо і віднімемо 1. Поділивши
почленно
![]() на
на![]() ,
отримаємо алгебраїчну суму двох
табличних інтегралів:
,
отримаємо алгебраїчну суму двох
табличних інтегралів:

8.
![]() .
.
Використаємо
формулу тригонометрії:
![]() .
.
Тоді

Завдання для самостійної роботи
Обчислити інтеграли:
1.
 ;
;
2.
![]() ;
;
3.
 ;
;
4.
![]() ;
;
5.
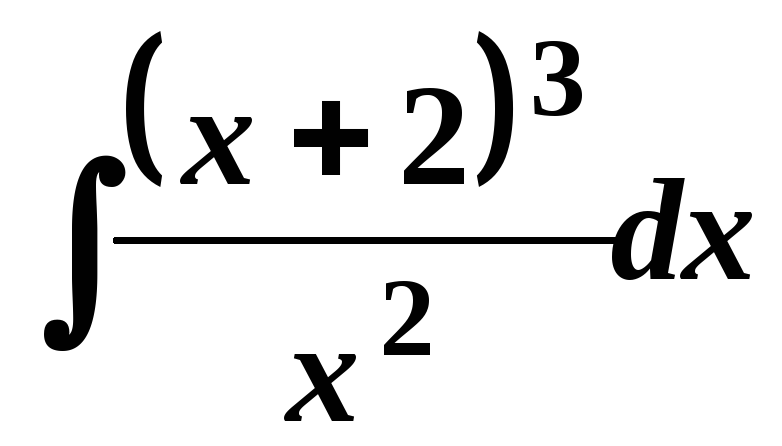 ;
;
6.
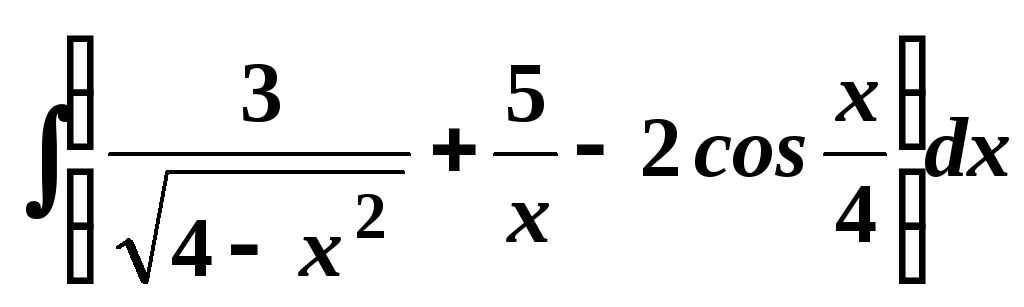 ;
;
7.
![]() ;
;
8.
 ;
;
9.
 ;
;
10.
 .
.
3.2. Метод підстановки (заміни змінної)
Заміна змінної у невизначеному інтегралі виконується за допомогою підстановок двох типів:
1.
Інтеграл
![]() зображають у вигляді:
зображають у вигляді:
![]() ,
,
де
функція
![]() має обернену функцію
має обернену функцію![]() і для функції
і для функції![]() відома первісна
відома первісна![]() .
.
Тоді
 .
.
2.
Інтеграл
![]() записують у вигляді
записують у вигляді
![]() ,
,
в
якому для функції
![]() відома первісна
відома первісна![]() .
.
Тоді

![]()
В обох випадках досягається мета спростити вихідний інтеграл та привести його до табличного інтегралу.
Зразки розв’язування задач
Обчислити інтеграли.
1.
 .
.
Поклавши
![]() ,
знайдемо
,
знайдемо![]() .
Ця підстановка призведе до того, що
під знаком синуса з’явиться
змінна інтегрування, а не корінь з неї.
Отримаємо:
.
Ця підстановка призведе до того, що
під знаком синуса з’явиться
змінна інтегрування, а не корінь з неї.
Отримаємо:

Відповідь
повинна бути виражена через початкову
змінну
![]() .
Підставляючи в результат інтегрування
.
Підставляючи в результат інтегрування![]() ,
дістанемо:
,
дістанемо:
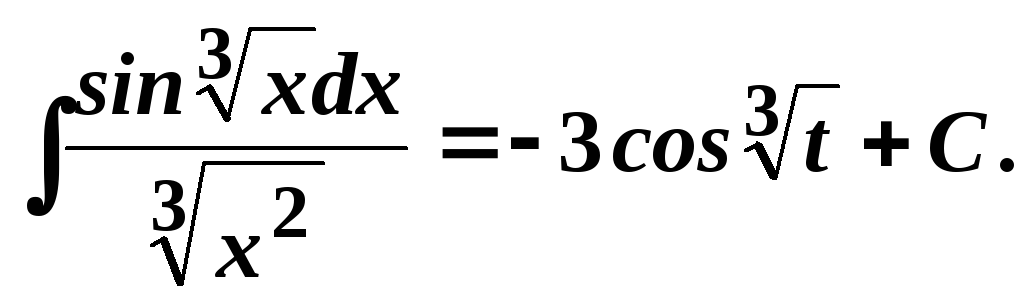
2.


3.

![]()
4.

![]()
5.

6.

7.

8.

![]()
9.

10.

![]()
11.


12.


Завдання для самостійної роботи
Обчислити інтеграли:
1.
 ;
;
2.
![]() ;
;
3.
 ;
;
4.
![]() ;
;
5.
 ;
;
6.
 ;
;
7.
![]() ;
;
8.
 ;
;
9.
 ;
;
10.
![]() ;
;
11.
 ;
;
12.
![]() .
.
3.3. Метод інтегрування частинами
Якщо
![]() та
та![]() - функції, що мають на деякому проміжку
неперервні похідні, то справедлива
формула інтегрування частинами:
- функції, що мають на деякому проміжку
неперервні похідні, то справедлива
формула інтегрування частинами:
![]() .
.
Тут
вважається заданою ліва частина формули,
тобто
![]() .
Обчислення цього інтеграла зводиться
до знаходження диференціала
.
Обчислення цього інтеграла зводиться
до знаходження диференціала
![]() функції
функції![]() та функції
та функції![]() за відомим її диференціалом
за відомим її диференціалом![]() .
Функція
.
Функція![]() визначається неоднозначно, з точністю
до довільної сталої
визначається неоднозначно, з точністю
до довільної сталої![]() ,
тому вибирають ту функцію, яка має
найпростіший вигляд (як правило,
покладають
,
тому вибирають ту функцію, яка має
найпростіший вигляд (як правило,
покладають![]() ).
).
Методом інтегрування частинами зручно обчислювати такі типи інтегралів:
1)
інтеграли виду
![]() ,
,![]() ,
,![]() ,
,![]() ,
де
,
де![]() - многочлен
- многочлен![]() -ого
степеня від
-ого
степеня від![]() ,
,![]() - дійсне число . У цих інтегралах за
- дійсне число . У цих інтегралах за![]() слід взяти множник
слід взяти множник![]() ,
а за
,
а за![]() - вираз, що залишився;
- вираз, що залишився;
2)
інтеграли виду
![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
У цих інтегралах слід взяти за
.
У цих інтегралах слід взяти за![]() множник
множник![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
а за
,
а за![]() -
-![]() ;
;
3)
інтеграли виду
![]() ,
,![]() ,
де
,
де![]() - дійсні числа.
- дійсні числа.
Тут після двократного застосування формули інтегрування частинами утворюється лінійне рівняння відносно шуканого інтеграла. Розв’язуючи це рівняння, знаходять інтеграл.
