
Arkhitektura_EVM_uchebnoe_posobie
.pdf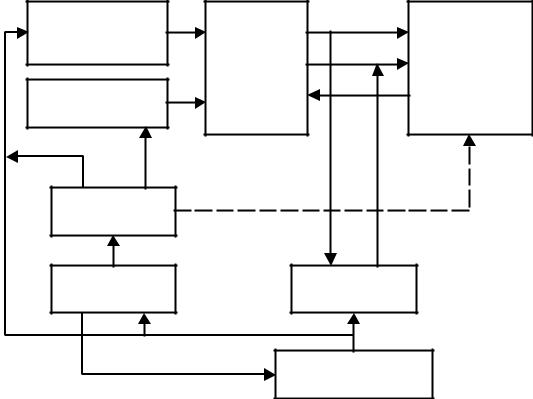
Селектор регистров |
|
|
|
1-го операнда |
Массив |
|
|
и результата |
Арифметико- |
||
|
регистров |
логическое |
|
|
общего |
||
|
устройство |
||
Селектор регистра |
назначения |
||
|
|||
2-го операнда |
|
|
|
Дешифратор кода |
|
|
|
операции |
|
|
|
Регистр команды |
|
Регистр данных |
Основная память
Рис. 1.7. Архитектура вычислительной машины на базе регистров общего назначения
Операции загрузки регистров из памяти и сохранения содержимого регистров в памяти идентичны таким же операциям с аккумулятором. Отличие состоит в этапе выбора нужного регистра, обеспечиваемого соответствующими селекторами.
К достоинствам регистровых АСК следует отнести: компактность получаемого кода, высокую скорость вычислений за счет замены обращений к основной памяти на обращения к быстрым регистрам. Хотя, данная архитектура требует более длинных инструкций по сравнению с аккумуляторной архитектурой.
Примерами машин на базе РОН могут служить CDC 6600, IBM 360/370, PDP-11, все современные персональные компьютеры. Правомочно утверждать, что в наши дни этот вид архитектуры системы команд является преобладающим.
Архитектура с выделенным доступом к памяти
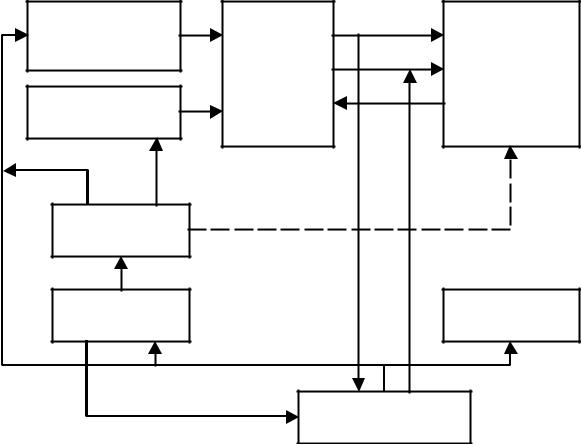
Состав и информационные тракты ЭВМ с выделенным доступом к памяти показаны на рис. 1.8.
В архитектуре с выделенным доступом к памяти обращение к основной памяти возможно только с помощью двух специальных команд: load и store. В английской транскрипции данную архитектуру называют Load/Store architecture.
30
Селектор регистров |
|
|
|
1-го операнда |
Массив |
|
|
и результата |
Арифметико- |
||
|
регистров |
логическое |
|
|
общего |
||
|
устройство |
||
Селектор регистра |
назначения |
||
|
|||
2-го операнда |
|
|
|
Дешифратор кода |
|
|
|
операции |
|
|
|
Регистр команды |
|
Регистр данных |
|
|
|
Основная память |
Рис. 1.8. Архитектура вычислительной машины с выделенным доступом к памяти
Команда load (загрузка) обеспечивает считывание значения из основной памяти и занесение его в регистр процессора (в команде обычно указывается адрес ячейки памяти и номер регистра). Пересылка информации в противоположном направлении производится командой store (сохранение). Операнды во всех командах обработки информации могут находиться только в регистрах процессора (чаще всего в регистрах общего назначения). Результат операции также заносится в регистр. В архитектуре отсутствуют команды обработки, допускающие прямое обращение к основной памяти. Допускается наличие в АСК ограниченного числа команд, где операнд является частью кода команды.
Вопросы к главе 1
1.Что называют электронно-вычислительной машиной?
2.Что такое архитектура ЭВМ?
3.Приведите основные характеристики ЭВМ.
4.Приведите классификацию ЭВМ по быстродействию.
5.Назовите основные компоненты типичной фон-неймановской ЭВМ.
6.Укажите основные концепции фон-неймановской ЭВМ.
7.Что представляет собой цикл команды процессора?
31
8.Назовите этапы выполнения цикла процессора.
9.Что называется системой команд и архитектурой системы команд
ЭВМ?
10.Приведите основные концепции CISC-архитектуры?
11.Приведите основные концепции RISC-архитектуры?
12.Чем характеризуется стековая АСК?
13.Чем характеризуется аккумуляторная АСК?
14.Чем характеризуется регистровая АСК?
15.Приведите характеристики АСК с выделенным доступом к памяти.
32
Глава 2
АРИФМЕТИКО-ЛОГИЧЕСКИЕ ОСНОВЫ ЭВМ
2.1. Системы счисления
Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
Различают позиционные и непозиционные системы счисления.
Из непозиционных наиболее распространенной является римская система счисления. В ней базовые числа обозначены заглавными латинскими буквами: 1 – 1, 5 – V, 10 – X, 50 – L, 100 – C, 500 – D, 1000 – M. Все другие числа строят-
ся из комбинаций базовых чисел в соответствии со следующими правилами:
если цифра меньшего значения стоит справа от большей цифры, то их значение суммируется; если слева – то меньшее значение вычитается из большего;
цифры I, X, C и M могут следовать подряд не более трех раз каждая; цифры V, L и D могут использоваться в записи числа не более одного раза.
Например, запись XIX соответствует числу 19, MDXLIX – числу 1549. Запись чисел в такой системе громоздка и неудобна. Отсутствие нуля, знаков для чисел больше М не позволяют римскими цифрами записать любое число. Поэтому римская система счисления используется лишь для нумерации.
В позиционных системах каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:
A |
n |
= a |
a |
Ka a |
. a |
a |
Ka |
−k |
= a |
m−1 |
Nm−1 +a |
m−2 |
Nm−2 +K+a |
−k |
N−k , |
или |
|
m−1 m−2 |
1 0 |
|
−1 −2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
m−1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
An = ∑ai Ni |
|
|
|
|
(2.1) |
|||||
i=−k
где ai – i-я цифра числа, k – количество цифр в дробной части числа, m – коли-
чество цифр в целой части числа, N – основание системы счисления. Основание системы счисления N показывает, во сколько раз «вес» i-го раз-
ряда больше (i-1) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
Пример 2.1. В соответствии с формулой (2.1) число А10=634.51 формируется из
цифр с весами рядов:
A10 = 6·102+3·101+4·100+5·10-1+1·10-2
Во всех современных ЭВМ для представления числовой информации используется двоичная система счисления. Это обусловлено
более простой реализацией алгоритмов выполнения арифметических и логических операций;
33
более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
экономичностью аппаратурной реализации всех схем ЭВМ.
При N=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр: 0 и 1.
Кроме двоичной системы счисления широкое распространение получили и производные системы:
шестнадцатеричная - {0, 1, 2, ...9, А, В, С, D, Е, F}. Здесь шестнадцате-
ричная цифра А обозначает число 10, В – число 11, ..., F – число 15;
восьмеричная (от слова восьмерик) – {0, 1, 2, 3, 4, 5, 6, 7}. Она широко ис-
пользуется во многих специализированных ЭВМ.
Пример 2.2. Число в двоичной, восьмеричной и шестнадцатеричной системах
счисления имеет следующее представление:
А2 = 1101001,101 = 1·26+1·25+0·24+1·23+0·22+0·21+1·20+1·2-1+0·2-2+1·2-3;
А8 = 237,5 = 2·82+3·81+7·80+5·8-1; A16 = 5B,A = 5·161+11·160+10·16-1.
Представление чисел в различных системах счисления допускает однозначное преобразование их из одной системы в другую. В ЭВМ перевод из одной системы в другую осуществляется автоматически по специальным программам. Правила перевода целых и дробных чисел отличаются.
Правило 1. Целое число с основанием N1 переводится в систему счисления с основанием N2 путем последовательного деления числа AN1 на основание N2,
записанного в виде числа с основанием N1, до получения остатка. Полученное частное следует вновь делить на основание N2, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя. Полученные остатки от деления и последнее частное записываются в порядке, обратном полученному при делении. Сформированное число и будет являться числом с основанием N2.
Пример 2.3. Дано число A10 = 47, перевести его в двоичную, восьмеричную и
шестнадцатеричную систему счисления. |
|
|
|
|
|
|
|
|
|
|||
p=2 |
Целая часть |
|
47 |
|
23 |
|
11 |
|
5 |
2 |
1 |
0 |
Остаток |
|
|
|
1 |
|
1 |
|
1 |
1 |
0 |
1 |
|
|
Разряд |
|
|
|
a0 |
|
a1 |
a2 |
a3 |
a4 |
a5 |
|
p=8 |
Целая часть |
|
47 |
|
5 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Остаток |
|
|
|
7 |
|
5 |
|
|
|
|
|
|
|
Разряд |
|
|
|
a0 |
|
a1 |
|
|
|
|
|
p=16 |
Целая часть |
|
47 |
|
16 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Остаток |
|
|
|
15 |
|
2 |
|
|
|
|
|
|
|
Разряд |
|
|
|
a0 |
|
a1 |
|
|
|
|
|
Ответ: A2 = 101111, A8 = 57, A16 = 2F.
34
Правило 2. Дробное число с основанием N1 переводится в систему счисления с основанием N2 путем последовательного умножения AN1 на основание
N2, записанное в виде числа с основанием N1. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата, представляющего число AN1 в системе счисления N2. Преобразование продолжается до тех пор, пока
после очередного умножения дробная часть не окажется равной нулю (что означает точное преобразование) или пока не получим достаточное количество разрядов (что означает приближенное преобразование).
Пример 2.4. Дано число A10 = 0,23, перевести его в двоичную, восьмеричную и шестнадцатеричную систему счисления.
p=2 |
Дробная часть |
|
0,23 |
|
0,46 |
|
0,92 |
|
0,84 |
|
0,68 |
|
0,36 |
|
|
0,72 |
|
0,44 |
Целое |
|
|
|
0 |
|
0 |
|
1 |
|
1 |
|
1 |
|
|
0 |
|
1 |
|
|
Разряд |
|
|
|
a-1 |
|
a-2 |
|
a-3 |
|
a-4 |
|
a-5 |
|
a-6 |
a-7 |
||
p=8 |
Дробная часть |
|
0,23 |
|
0,84 |
|
0,72 |
|
0,76 |
|
0,08 |
|
0,64 |
|
|
0,12 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Целое |
|
|
|
1 |
|
6 |
|
5 |
|
6 |
|
0 |
|
|
5 |
|
|
|
|
Разряд |
|
|
|
a-1 |
|
a-2 |
|
a-3 |
|
a-4 |
|
a-5 |
|
a-6 |
|
|
|
p=16 |
Дробная часть |
|
0,23 |
|
0,68 |
|
0,88 |
|
0,08 |
|
0,28 |
|
0,48 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Целое |
|
|
|
3 |
|
10 |
|
14 |
|
1 |
|
4 |
|
|
|
|
|
|
|
Разряд |
|
|
|
a-1 |
|
a-2 |
|
a-3 |
|
a-4 |
|
a-5 |
|
|
|
|
|
Ответ: A2 = 0,0011101…, A8 = 0,165605…, A16 = 0,3AE14…
Правило 3. Для преобразования целого числа Zp→Zq в том случае, если системы счисления связаны соотношением q=pr, где r – целое число, большее 1, достаточно Zp разбить справа налево на группы по r цифр и каждую из них независимо перевести в систему q.
Правило 4. Для преобразования целого числа Zp→Zq в том случае, если системы счисления связаны соотношением p=qr, где r – целое число, большее 1, достаточно каждую цифру Zp заменить соответствующим r-разрядным числом в системе счисления q, дополняя его при необходимости незначащими нулями слева до группы в r цифр.
Так как двоичная, восьмеричная и шестнадцатеричная системы связаны через степени числа 2, то преобразования между ними можно выполнять другим более простым способом. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные коды цифр тетрадами (по 4 двоичных разряда) и триадами (по 3 двоичных разряда) – для восьмеричных цифр. Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от границы целой и дробной частей на тетрады – для последующей записи цифр в шестнадцатеричном представлении, на триады – для записи их
35

значений восьмеричными цифрами. Недостающие разряды (для целой части слева, для дробной части справа) дополняют нулями.
В табл. 2.1 приведено соответствие между числами десятичной, двоичной, восьмеричной и шестнадцатеричной системы счисления.
|
|
|
Таблица 2.1 |
Соответствие между числами в разных системах счисления |
|||
|
|
|
|
Десятичная |
Двоичная |
Восьмеричная |
Шестнадцатеричная |
0 |
0000 |
00 |
0 |
1 |
0001 |
01 |
1 |
2 |
0010 |
02 |
2 |
3 |
0011 |
03 |
3 |
4 |
0100 |
04 |
4 |
5 |
0101 |
05 |
5 |
6 |
0110 |
06 |
6 |
7 |
0111 |
07 |
7 |
8 |
1000 |
10 |
8 |
9 |
1001 |
11 |
9 |
10 |
1010 |
12 |
A |
11 |
1011 |
13 |
B |
12 |
1100 |
14 |
C |
13 |
1101 |
15 |
D |
14 |
1110 |
16 |
E |
15 |
1111 |
17 |
F |
Пример 2.5. Дано число A10 = 47,23, перевести его в двоичную, восьмеричную и
шестнадцатеричную систему счисления.
A2 = 101111,0011101 = 0010 1111,0011 1010 = 101 111,001 110 100
Используя табл. 2.1, получим:
A8 = 57,164
A16 = 2F,3A.
Так как все действия в ЭВМ выполняются, как правило, в двоичной системе счисления, то, очевидно, для процесса преобразования из 10-ичной в 2- ичную систему счисления представленные (A10→B2) правила перевода являются неприемлемыми. Алгоритмы перевода A10→B2 реализуемые на ЭВМ, как и для других систем счисления, являются рекуррентными и основаны на другом представлении позиционного числа.
Пусть имеем число в позиционной системе счисления с основанием N
amam−1 Ka1a0 . a−1a−2 Ka−k .
Тогда целая часть
A = amam−1 Ka1a0 = (K(am N +am−1 ) N +K+a1 ) N +a0 ,
дробная часть
B = 0,a−1a−2 Ka−k = (K(a−k N +a−(k−1) ) N +K+a−1 ) N .
N .
36
Преобразование целой части, таким образом, начинается с самого старшего разряда числа, преобразование дробной части – с самого младшего разряда числа.
При этом необходимо все цифры числа и основание N представить в новой системе счисления и все арифметические действия выполнить в новой системе счисления.
Пример 2.6. Перевести число 4320,31 из 5-ричной системы счисления в троич-
ную, а результат – в 10-ричную систему счисления
Вариант 1.
Переведем целую часть в троичную систему счисления (все действия выполняем в 5-ричной системе счисления).
Для выполнения арифметических действий построим таблицы сложения и умножения в 5-ричной системах счисления.
Таблица сложения для 5- |
|
|
|
Таблица умножения для 5- |
||||||||||||||||||
ричной системы счисления |
|
|
|
ричной системы счисления |
||||||||||||||||||
+ |
0 |
1 |
2 |
|
3 |
|
4 |
|
|
|
× |
0 |
1 |
2 |
3 |
4 |
||||||
0 |
0 |
|
1 |
2 |
|
3 |
|
4 |
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
|||||
1 |
1 |
|
2 |
3 |
|
4 |
|
10 |
|
|
|
1 |
0 |
1 |
2 |
3 |
4 |
|||||
2 |
2 |
|
3 |
4 |
|
10 |
|
11 |
|
|
|
2 |
0 |
2 |
4 |
11 |
13 |
|||||
3 |
3 |
|
4 |
10 |
|
11 |
|
12 |
|
|
|
3 |
0 |
3 |
11 |
14 |
22 |
|||||
4 |
4 |
|
10 |
11 |
|
12 |
|
13 |
|
|
|
4 |
0 |
4 |
13 |
22 |
31 |
|||||
4320 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 |
|
|
1240 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
11 |
|
230 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
11 |
|
|
14 |
|
22 |
|
|
41 |
|
3 |
|
|
|
|
|
|
|
|
|
|||
22 |
|
|
14 |
10 |
|
|
3 |
|
|
12 |
3 |
|
|
|
|
|
|
|
||||
22 |
|
|
0 |
3 |
11 |
|
11 |
2 |
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
2 |
|
11 |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
43205 = 2102003
Переведем дробную часть в троичную систему счисления:
Дробная часть |
0,31 |
0,43 |
0,34 |
0,12 |
Целое |
|
1 |
2 |
2 |
0,315 ≈ 0,1223 |
|
|
|
|
4320,315 ≈ 210200,1223
Переведем оба числа в десятичную систему счисления:
4320.315 = 4 53 + 3 52 + 2 51 + 0 50 + 3 5-1 + 1 5-2 =
=4 125 + 3 25 + 2 5 + 3/5 + 1/25 =
=500 + 75 + 10 + 0,6 + 0,04 = 585,64
210200,1223 = 2 35 + 1 34 + 0 33 + 2 32 + 0 31 + 0 30 + 1 3-1 + 2 3-2 + 2 3-3 =
=2 243 + 1 81 + 2 9 + 1/3 + 2/9 + 2/27 =
=486 + 81 + 18 + 17/27 ≈ 585 + 0,63 = 585,63
37

Вариант 2.
Представим исходное число в троичной системе счисления выполнив все дей-
ствия в троичной системе счисления (при этом 35 = 103, 45 = 113, 55 = 123).
Для выполнения арифметических действий построим таблицы сложения и ум-
ножения в троичной системах счисления.
Таблица сложения для троичной системы счисления
+ |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
1 |
1 |
2 |
10 |
2 |
2 |
10 |
11 |
Таблица умножения для троичной системы счисления
× |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
2 |
0 |
2 |
11 |
4320,315 = (4 53 + 3 52 + 2 51 + 0 50 + 3 5-1 + 1 5-2)5 =
=(11 123 + 10 122 + 2 121 + 0 50 + 10 12-1 + 1 5-2)3 =
=(((11 12 + 10) 12 + 2) 12 + 0 + (1/12 + 10)/12)3 =
=(((202 + 10) 12 + 2) 12 + (121/12)/12)3 =
=((212 12 + 2) 12 + 121/221)3 =
=(11100 12 + 121/221)3 =
≈ (210200 + 0,122)3 = 210200,1223
Ответ: 4320,315 = 210200,1223 = 585,6310
2.2. Двоичная арифметика
Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Однако выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвиг. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации. Правила сложения двоичных цифр двух чисел А и В представлены в табл. 2.2.
Таблица 2.2
Правила сложения двоичных цифр
Значения двоичных |
Разряд |
Перенос в сле- |
||||
|
чисел А и В |
|
суммы |
дующий разряд |
||
аi |
|
bi |
|
Pi-1 |
Si |
Рi |
0 |
|
0 |
|
0 |
0 |
0 |
0 |
|
0 |
|
1 |
1 |
0 |
0 |
|
1 |
|
0 |
1 |
0 |
0 |
|
1 |
|
1 |
0 |
1 |
1 |
|
0 |
|
0 |
1 |
0 |
1 |
|
0 |
|
1 |
0 |
1 |
1 |
|
1 |
|
0 |
0 |
1 |
1 |
|
1 |
|
1 |
1 |
1 |
Здесь показаны правила сложения двоичных цифр ai, bi одноименных разрядов с учетом возможных переносов из предыдущего разряда pi-1.
Особенностью выполнения арифметических операций ЭВМ является то, что все четыре действия арифметики сводятся к операции сложения. Для реали-
38
зации машинных арифметических операций необходимо представить числа в машинных кодах: прямом, обратном, дополнительном. Обратный и дополнительный коды используются ЭВМ для представления отрицательных чисел с целью замены операции вычитания операцией сложений.
При записи чисел будем отделять знаковый разряд от значащих двоеточием для облегчения чтения машинных кодов. В ЭВМ никаких разделителей между знаком числа и его разрядами не существует.
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 для положительных чисел и 1 для отрицательных) перед его старшим числовым разрядом.
Пример 2.8. Представить числа A10 = +18 и B10 = –23 в виде прямого кода дво-
ичного числа. |
|
|
A10 = +18 |
A2 = +10010 |
A2 ПК = 0:10010 |
B10 = –23 |
B2 = –10111 |
B2 ПК = 1:10111 |
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы – нулями.
Пример 2.9. Представить числа A10 = +25 и B10 = –19 в виде обратного кода
двоичного числа. |
|
|
A10 = +25 |
A2 = +11001 |
A2 OK = A2ПК = 0:11001 |
B10 = –19 |
B2 = –10011 |
B2 OK = 1:01100 |
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда.
Пример 2.10. Представить числа A10 = +29 и B10 = –31 в виде дополнительного кода двоичного числа.
A10 = +29 |
A2 = +11101 |
A 2 ДК = A2 ОK = A2 ПК = 0:11101 |
B10 = –31 |
В2 = –11111 |
B 2 ДК = B2 OK + 1 = 1:00000+1 = 1:00001 |
Сложение двоичных чисел осуществляется последовательно и поразрядно. При выполнении сложения цифр необходимо соблюдать следующие правила:
1.Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
2.Знаковые разряды чисел участвуют в сложении так же, как и значащие.
3.Необходимые преобразования кодов производятся с изменением знаков
39
