
Arkhitektura_EVM_rekomendatsii
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к изучению курса «АРХИТЕКТУРА ЭВМ»
Донецк ДонНУ 2007
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ к изучению курса «АРХИТЕКТУРА ЭВМ»
(для студентов специальностей «Прикладная математика» и «Информатика», обучающихся по кредитно-модульной системе)
Утверждено на заседании кафедры
прикладной математики и теории систем управления
Протокол № __ от __.__.2007
Донецк ДонНУ 2007
ББК 32.973.2 УДК 681.34
Методические рекомендации к изучению курса «Архитектура ЭВМ (для студентов специальностей «Прикладная математика» и «Информатика» обучающихся по кредитно-модульной системе) / Сост. Ю.В. Шамарин, С.В. Блохин. – Донецк: ДонНУ, 2007. – 24с.
В методических рекомендациях содержатся сведения о цели и задании изучения курса, распределение учебных часов по видам занятий, перечень тем, которые изучаются в курсе. Приведены рекомендации по самостоятельной работе студентов, перечень вопросов для изучения теоретического материала, индивидуальные задания и пример их решения, методы контроля знаний студентов, предоставлен список литературы, необходимый для изучения курса.
Составители |
Ю.В. Шамарин, доц. |
|
С.В. Блохин, ст. преп. |
Отв. за выпуск |
С.В. Мышко, проф. |
Предисловие
Электронно-вычислительные машины (ЭВМ) являются в современном обществе самыми востребованными ресурсами. Войдя в человеческую жизнь, компьютеры сейчас стали неотъемлемой частью нашей цивилизации. И хотя первая ЭВМ с автоматическим программным управлением была создана чуть более полувека назад, к настоящему моменту уже насчитывается пять поколений вычислительных машин. Столь бурного развития, вероятно, не претерпевала ни одна технология.
Дисциплина «Архитектура ЭВМ» является базовой для многих направлений исследований в области прикладной математики и информационных технологий, что определяет необходимость изучения данной дисциплины студентами специальностей «Прикладная математика» и «Информатика».
Целью курса является ознакомление студентов с общими принципами построения современных ЭВМ, архитектурными особенностями микропроцессоров (МП), которые используются в современных ЭВМ.
Прослушав курс, студент должен знать: системы счисления и кодирование в них числовой информации, архитектуру МП, последовательности работы узлов МП, виды адресации и их реализации, организацию системных обменов информацией между узлами ЭВМ.
Для изучения дисциплины предполагается чтение лекций, проведение лабораторных работ с привлечением компьютерной техники, а также самостоятельная работа студентов с выполнением индивидуальных заданий.
Текущий контроль знаний предполагает проведение аудиторных контрольных работ. Итоговый контроль знаний предполагает проведение письменных модульных контрольных работ в конце каждого модуля и проведение итогового письменного экзамена.
1.Учебная программа курса «Архитектура ЭВМ». Литература
1.1.Программа курса
1. Введение. Системы счисления.
Вводная лекция. Задача и цель курса. Понятие о системе счисления. Правила перевода чисел из одной системы счисления в другую.
2. Двоичная арифметика.
Представление отрицательных чисел в двоичной системе счисления. Выполнение арифметических действий в двоичной системе счисления. Двоичнодесятичное представление чисел.
3. Архитектура ЭВМ. История.
Основные положения архитектуры ЭВМ. Характеристики ЭВМ. История создания ЭВМ. Основные этапы создания ЭВМ.
3
4. Фон-неймановская архитектура.
Основные положения фон-неймановской архитектуры. Компоненты классической ЭВМ.
5. Архитектура системы команд.
Определение архитектуры системы команд. Концепции CISC, RISC, VLIW архитектур. Характеристики и структура стековой, аккумуляторной, регистровой архитектур и архитектуры с выделенным доступом к памяти.
6. Логические схемы. Минимизация логических схем.
Понятие логической функции. Основные законы логики. Карты Карно. Минимизация логических функций.
7. Микропроцессор. Структура. Адресация.
Архитектура и структура микропроцессора на примере Intel 8086 (К1810). Адресация. Система команд микропроцессора Intel 8086. Группы команд. Форматы команд. Кодирование команд. Кодирование операндов команд.
8. Основная память.
Характеристики основной памяти. Кэш-память. Уровни кэш-памяти. Алгоритмы актуализации данных в кэш-памяти. Внешняя память. Виды внешней памяти. Характеристики внешней памяти. Организация массивов данных.
9. Средства ввода/вывода.
Системы визуального отображения информации. Принтер. Сканер. Вывод аудиоинформации.
10. Современные тенденции развития ЭВМ.
Основные направления и тенденции развития и построения современных ЭВМ.
1.2. Список литературы
Основная литература
1.Бройдо В.Л., Ильина О.П. Архитектура ЭВМ. – СПб.: Питер, 2005. –
720 с.
2.Методические указания к изучению курса «Архитектура ЭВМ (для студентов специальностей «Прикладная математика» и «Информатика») / Сост. Ю.В. Шамарин, С.В. Блохин. – Донецк: ДонНУ, 2007. – 44с.
3.Таненбаум Э. Архитектура компьютера. – СПб.: Питер, 2003. – 697 с.
4.Цилькер Б.Я., Орлов С.А. Организация ЭВМ и систем. – СПб.: Питер, 2004. – 668 с.
Дополнительная литература
1.Микропроцессоры. Архитектура и проектирование микро-ЭВМ: Организация вычислительных процессов. Под ред. Л.Н. Преснухина. – М. Высшая школа, 1986. – Т1. – 494 с.
2.Микропроцессоры. Средства сопряжения: Контролирующие и инфор- мационно-управляющие системы. Под ред. Л.Н. Преснухина. – М.: Высшая школа, 1986. – Т2. – 383 с.
3.Микропроцессоры. Средства отладки, лабораторный практикум и за-
4
дачник. Под ред. Л.Н. Преснухина. – М.: Высшая школа, 1986. – Т3. – 353 с.
4.Черняк Н.Г. и др. Архитектура вычислительных систем и сетей: Учеб. пособие. – М.: Финансы и статистика, 1986. – 318 с.
5.Балашов Е.Н., Григорьев В.Л., Петров Г.А. Микро- и мини ЭВМ. – Л.: Энергоатомиздат, 1984. – 376 с.
6.Жмакин А.П. Архитектура ЭВМ. – СПб.: БХВ-Петербург, 2006. – 320 с.
7.Микропроцессорный комплект К1810. Структура, программирование, применение. – М.: Высшая школа, 1990. – 269 с.
8.Юров В. Assembler. – СПб.: Питер, 2002. – 624 с.
2.Модульное планирование
|
|
Количество часов отведенных на |
||
|
Тема |
|
Лабора- |
Самостоя- |
|
Лекции |
торные |
тельную |
|
|
|
|||
|
|
|
занятия |
работу |
|
Модуль 1 |
|
|
|
|
|
|
|
|
1. |
Введение. Системы исчисления. |
2 |
2 |
7 |
2. |
Двоичная арифметика. Форматы данных. |
2 |
4 |
2 |
3. |
Архитектура ЭВМ. История. |
2 |
0 |
0 |
4. |
Фон-неймановская архитектура. |
2 |
0 |
0 |
5. |
Архитектура системы команд. |
2 |
0 |
2 |
6. |
Логические схемы. Минимизация логиче- |
2 |
2 |
4 |
ских схем. |
|
|
|
|
|
Модуль 2 |
|
|
|
|
|
|
|
|
7. |
Микропроцессор. Структура. Адресация. |
6 |
6 |
12 |
8. |
Основная память |
6 |
0 |
5 |
9. |
Средства ввода/вывода. |
2 |
0 |
5 |
10. Современные тенденции развития ЭВМ. |
2 |
0 |
0 |
|
|
Итого |
28 |
14 |
37 |
3. Задания для индивидуальных работ и примеры их решения
3.1. Индивидуальная работа №1. Системы счисления
Задание. Даны два числа Z1 и Z2 в 5-ричной системе счисления (табл. 1). Необходимо:
1)перевести их в 3-ичную методом деления и рекуррентным методом;
2)сложить числа в 5-ричной и в 3-ичной системах счисления;
3)перевести полученные результаты из 5-ричной и 3-ичной в 10-ричную систему счисления.
5
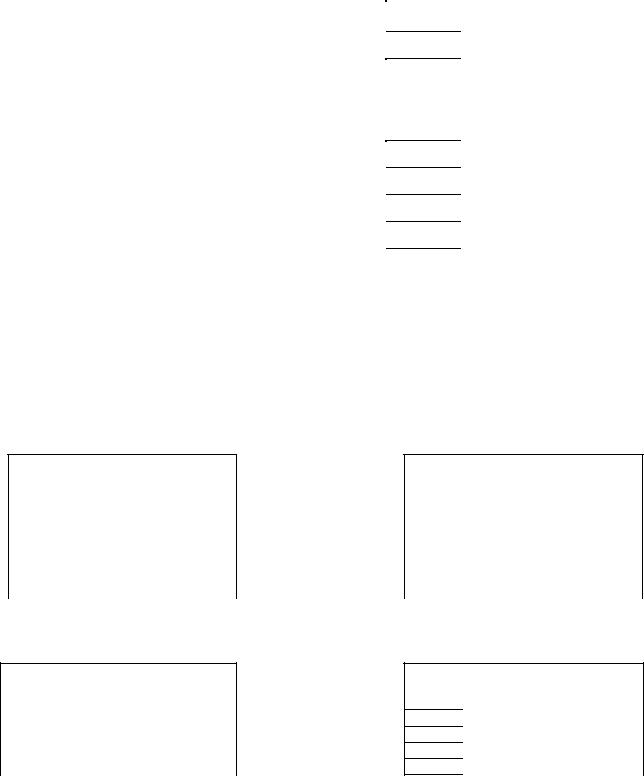
|
Варианты заданий для индивидуального задания №1 |
Таблица 1 |
||||
|
|
|||||
№ |
Z1 |
Z2 |
|
№ |
Z1 |
Z2 |
варианта |
|
варианта |
||||
|
|
|
|
|
||
1 |
4444 |
3330 |
|
11 |
4344 |
3430 |
|
|
|
|
|
|
|
2 |
4443 |
3331 |
|
12 |
4343 |
3431 |
|
|
|
|
|
|
|
3 |
4442 |
3332 |
|
13 |
4342 |
3432 |
|
|
|
|
|
|
|
4 |
4441 |
3333 |
|
14 |
4341 |
3433 |
|
|
|
|
|
|
|
5 |
4440 |
3334 |
|
15 |
4340 |
3434 |
|
|
|
|
|
|
|
6 |
4434 |
3340 |
|
16 |
4334 |
3440 |
|
|
|
|
|
|
|
7 |
4433 |
3341 |
|
17 |
4333 |
3441 |
|
|
|
|
|
|
|
8 |
4432 |
3342 |
|
18 |
4332 |
3442 |
|
|
|
|
|
|
|
9 |
4431 |
3343 |
|
19 |
4331 |
3443 |
|
|
|
|
|
|
|
10 |
4430 |
3344 |
|
20 |
4330 |
3444 |
|
|
|
|
|
|
|
Пример решения
Пусть даны числа Z1=4321 и Z2=3214.
Для выполнения арифметических действий построим таблицы сложения и таблицу умножения в 5-ричной (рис. 1) и 3-ичной системах счисления (рис. 2).
Таблица сложения для 5-ричной системы счисления
+ |
0 |
1 |
2 |
3 |
4 |
0 |
0 |
1 |
2 |
3 |
4 |
1 |
1 |
2 |
3 |
4 |
10 |
2 |
2 |
3 |
4 |
10 |
11 |
3 |
3 |
4 |
10 |
11 |
12 |
4 |
4 |
10 |
11 |
12 |
13 |
Таблица умножения для 5-ричной системы счисления
× |
0 |
1 |
2 |
3 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
4 |
2 |
0 |
2 |
4 |
11 |
13 |
3 |
0 |
3 |
11 |
14 |
22 |
4 |
0 |
4 |
13 |
22 |
31 |
Рис. 1. Таблицы сложения и умножения для 5-ричной системы счисления
Таблица сложения для 3-ичной системы счисления
+ |
0 |
1 |
2 |
0 |
0 |
1 |
2 |
1 |
1 |
2 |
10 |
2 |
2 |
10 |
11 |
Таблица умножения для 3-ичной системы счисления
× |
0 |
1 |
2 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
2 |
0 |
2 |
11 |
Рис. 2. Таблицы сложения и умножения для 3-ричной системы счисления
1) Переведем Z1 и Z2 в 3-ичную систему счисления методом деления. Все действия выполняем в 5-ричной системе счисления пользуясь таблицей умножения и таблицей сложения.
6
4321 |
3 |
|
|
|
|
3214 |
3 |
|
|
|
|
3 |
1240 |
3 |
|
|
|
3 |
1034 |
3 |
|
|
|
13 |
11 |
230 |
3 |
|
|
21 |
3 |
143 |
3 |
|
|
11 |
14 |
22 |
41 |
3 |
|
14 |
23 |
14 |
31 |
3 |
|
22 |
14 |
10 |
3 |
12 |
3 |
24 |
22 |
3 |
3 |
10 |
3 |
22 |
0 |
3 |
11 |
11 |
2 |
24 |
14 |
3 |
1 |
3 |
1 |
1 |
|
2 |
11 |
1 |
|
2 |
14 |
0 |
|
2 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
Получили 43215 = 2102013 и 32145 = 1210023.
Переведем исходные числа в 3-ичную систему счисления рекуррентным методом. Все арифметические действия выполняем в троичной системе счисле-
ния (при этом 310 = 103, 410 = 113, 510 = 123).
43215 = (4 53 + 3 52 + 2 51 + 1 50)5 = (11 123 + 10 122 + 2 121 + 1 120)3 = (((11 12 + 10) 12 + 2) 12 + 1) 3 = (((202 + 10) 12 + 2) 12 + 1) 3 = ((212 12 + 2) 12 + 1) 3 = (11100 12 + 1)3 = (210200 + 1)3 = 2102013
32145 = (3 53 + 2 52 + 1 51 + 4 50)5 = (10 123 + 2 122 + 1 121 + 11 120)3 = (((10 12+2) 12 +
1) 12 + 11) 3 = (((120 + 2) 12 + 1) 12 + 11)3 = ((122 12 + 1) 12 + 11) 3 = (10011 + 1) 12 + 11) 3 = (10012 12 + 11) 3 = (120221 + 11) 3 = 121002 3
Получили 43215 = 2102013 и 32145 = 1210023.
2) Сложим исходные числа в 5-ричной системе счисления, а полученные в 3-ичной.
+43215 |
+ 2102013 |
|
32145 |
1210023 |
|
130405 |
|
11012103 |
3) Переведем полученные результаты в 10-чную систему счисления.
130405 = 1 54 + 3 53 + 0 52 + 4 51 + 0 50 = 1 625 + 3 125 + 4 5 = 625 + 375 + 20 = 1020
11012103 = 1 36 + 1 35 + 0 34 + 1 33 + 2 32 + 1 31 + 0 30 = 1 729 + 1 243 + 1 27 + 2 9 + 1 3 = 729 + 243 + 27 + 18 +3 = 1020.
Ответ: (4321 + 3214)5 = (210201 + 121002)3 = 102010.
3.2. Индивидуальная работа №2. Логические функции
Задание. Дана логическая функция fn(x1, x2, x3, x4) заданная таблично (табл. 2). Необходимо:
1)построить дизъюнктивную форму;
2)построить конъюнктивную форму;
3)минимизировать любую из форм;
4)построить карту Карно и записать минимальную форму.
7
Таблица 2
Варианты заданий для индивидуального задания №2
x1 |
x2 |
x3 |
x4 |
f1 |
f2 |
f3 |
f4 |
f5 |
f6 |
f7 |
f8 |
f9 |
f10 |
f11 |
f12 |
f13 |
f14 |
f15 |
f16 |
f17 |
f18 |
f19 |
f20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример решения
Пусть задана таблично следующая логическая функция:
x1 |
x2 |
x3 |
x4 |
F(x1, x1, x3, x4) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
8
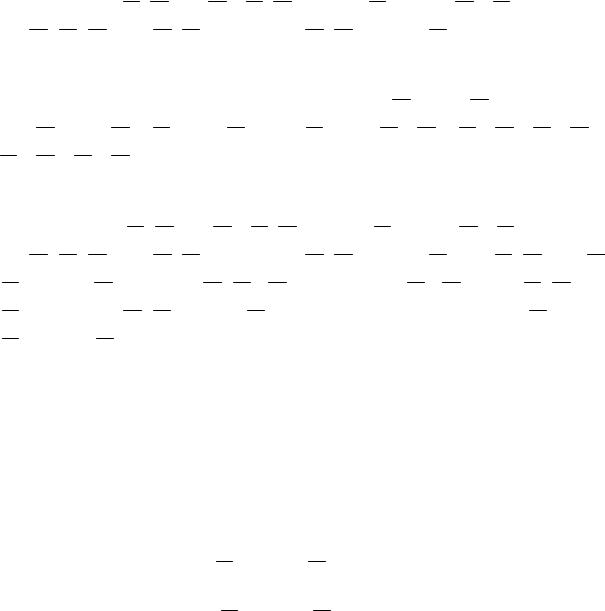
1) Построим дизъюнктивную форму логической функции:
F(x1, x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 .
2) Построим конъюнктивную форму логической функции
F(x1 , x2 , x3 , x4 ) =(x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 )
(x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 ) (x1 x2 x3 x4 )(x1 x2 x3 x4 ) .
3) Минимизируем форму (дизъюнктивную):
F(x1, x2 , x3 , x4 ) = x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 = x1 x2 x3 (x4 x4 )x1 x2 x3 (x4 x4 ) x1 x2 x3 (x4 x4 ) x1 x2 x3 (x4 x4 ) = x1 x2 x3
x1 x2 x3 x1 x2 x3 x1 x2 x3 ={по закону склеивания Fx2 Fx2 = F} =
x1 x3 x1 x3 .
4)Построим карту Карно для данной функции
|
|
|
|
|
|
|
|
x3x4 |
|
|
|
|
|
00 |
|
01 |
|
11 |
10 |
||
|
|
00 |
0 |
|
0 |
|
1 |
1 |
||
x1 |
x2 |
01 |
0 |
|
0 |
|
1 |
1 |
||
11 |
|
1 |
|
|
1 |
|
0 |
0 |
||
|
|
|
|
|
|
|||||
|
|
10 |
1 |
|
1 |
|
0 |
0 |
||
Тогда F(x1 , x2 , x3 , x4 ) = x1 x3 x1 x3 .
Ответ. F(x1 , x2 , x3 , x4 ) = x1 x3 x1 x3
3.3. Индивидуальная работа №3. Микропроцессор
Дан текст программы. Начальный адрес программы в сегменте равен 030Ch. Операция MOV кодируется значением 1000101w. Операция ADD кодируется значением 0000001w. Код команды LEA DI, mem равен BF. Код команды LEA SI, mem равен BE. Содержимое регистра DS равно 0AB0H. Код команды MOV BP, WORD равен BD, код команды MOV BX, WORD равен BB.
Необходимо:
1)отобразить представление исходных данных и команд в виде непрерывного фрагмента оперативной памяти (16-ричная система счисления);
2)указать способ адресации операндов;
3)логический и физический адрес адресуемой ячейки памяти;
4)содержимое регистров и памяти после выполнения команд МП.
9
