4.Единицы измерения емкости, определение единицы.

Фара́д (русское обозначение: Ф; международное обозначение: F; прежнее название — фара́да) — единица измерения электрической ёмкости в Международной системе единиц (СИ), названа в честь английского физика Майкла Фарадея^[1].

1 фарад равен ёмкости конденсатора, при которой заряд 1 кулон создаёт между его обкладками напряжение 1 вольт:

1 Ф = 1 Кл/1 В = I·T/U.

Ф = А² · с⁴ · кг⁻¹ · м⁻² = Дж/В² = Кл²/Дж = А · с / В = с/Ом.

Таким образом, конденсатор ёмкостью 1Ф, в идеале, может зарядиться до 1 В при зарядке током 1 А в течение 1 секунды.

Фарад — очень большая ёмкость для уединённого проводника. Ёмкостью 1 Ф обладал бы уединённый металлический шар, радиус которого равен 13 радиусам Солнца. Ёмкость же Земли (точнее, шара размером с Землю, используемого как уединённый проводник) составляет около 710 микрофарад.

Ионистор со взаимной ёмкостью в 1 фарад.

Промышленные конденсаторы имеют номиналы, измеряемые в микро-, нано- и пикофарадах и выпускаются ёмкостью до ста фарад; в звуковой аппаратуре используются гибридные конденсаторы ёмкостью до 40 фарад^[2].

5.Какова физическая природа сдвига фаз в цепях переменного тока, содержащих емкостные и индуктивные сопротивления?

§ 162. Сдвиг фаз между током и напряжением.

Проделаем следующий опыт. Возьмем описанный в § 153 осциллограф с двумя петлями и включим его в цепь так (рис. 305,а), чтобы петля 1 была включена в цепь последовательно с конденсатором, а петля 2 параллельно этому конденсатору. Очевидно, что кривая, получаемая от петли 1, изображает форму тока, проходящего через конденсатор, а от петли 2 дает форму напряжения между обкладками конденсатора (точками и), потому что в этой петле осциллографа ток в каждый момент времени пропорционален напряжению. Опыт показывает, что в этом случае кривые тока и напряжения смещены по фазе, причем ток опережает по фазе напряжение на четверть периода (на). Если бы мы заменили конденсатор катушкой с большой индуктивностью (рис. 305,б), то оказалось бы, что ток отстает по фазе от напряжения на четверть периода (на). Наконец, таким же образом можно было бы показать, что в случае активного сопротивления напряжение и ток совпадают по фазе (рис. 305,в).

Рис. 305. Опыт по обнаружению сдвига фаз между током и напряжением: слева – схема опыта, справа – результаты

В общем случае, когда участок цепи содержит не только активное, но и реактивное (емкостное, индуктивное или и то и другое) сопротивление, напряжение между концами этого участка сдвинуто по фазе относительно тока, причем сдвиг фаз лежит в пределах от дои определяется соотношением между активным и реактивным сопротивлениями данного участка цепи.

В чем заключается физическая причина наблюдаемого сдвига фаз между током и напряжением?

Если в цепь не входят конденсаторы и катушки, т. е. емкостным и индуктивным сопротивлениями цепи можно пренебречь по сравнению с активным, то ток следует за напряжением, проходя одновременно с ним через максимумы и нулевые значения, как это показано на рис. 305,в.

Если цепь имеет заметную индуктивность , то при прохождении по ней переменного тока в цепи возникает э. д. с. самоиндукции. Эта э. д. с. по правилу Ленца направлена так, что она стремится препятствовать тем изменениям магнитного поля (а следовательно, и изменениям тока, создающего это поле), которые вызывают э. д. с. индукции. При нарастании тока э. д. с. самоиндукции препятствует этому нарастанию, и потому ток позже достигает максимума, чем в отсутствие самоиндукции. При убывании тока э. д. с. самоиндукции стремится поддерживать ток и нулевые значения тока будут достигнуты в более поздний момент, чем в отсутствие самоиндукции. Таким образом, при наличии индуктивности ток отстает по фазе от тока в отсутствие индуктивности, а следовательно, отстает по фазе от своего напряжения.

Если активным сопротивлением цепи можно пренебречь по сравнению с ее индуктивным сопротивлением, то отставание тока от напряжения по времени равно(сдвиг фаз равен), т. е. максимумсовпадает с, как это показано на рис. 305,б. Действительно, в этом случае напряжение на активном сопротивлении, ибо, и, следовательно, все внешнее напряжениеуравновешивается э. д. с. индукции, которая противоположна ему по направлению:. Таким образом, максимумсовпадает с максимумом, т. е. наступает в тот момент, когдаизменяется быстрее всего, а это бывает, когда. Наоборот, в момент, когдапроходит через максимальное значение, изменение тока наименьшее, т. е. в этот момент.

Если активное сопротивление цепи не настолько мало, чтобы им можно было пренебречь, то часть внешнего напряженияпадает на сопротивлении, а остальная часть уравновешивается э. д. с. самоиндукции:. В этом случае максимумотстоит от максимумапо времени меньше, чем на(сдвиг фаз меньше), как это изображено на рис. 306. Расчет показывает, что в этом случае отставание по фаземожет быть вычислено по формуле

.                   (162.1)

При имееми, как это объяснено выше.

Рис. 306. Сдвиг фаз между током и напряжением в цепи, содержащей активное и индуктивное сопротивления

Если цепь состоит из конденсатора емкости , а активным сопротивлением можно пренебречь, то обкладки конденсатора, присоединенные к источнику тока с напряжением, заряжаются и между ними возникает напряжение. Напряжение на конденсатореследует за напряжением источника токапрактически мгновенно, т. е. достигает максимума одновременно си обращается в нуль, когда.

Зависимость между током и напряжениемв этом случае показана на рис. 307,а. На рис. 307,б условно изображен процесс перезарядки конденсатора, связанный с появлением переменного тока в цепи.

Рис. 307. а) Сдвиг фаз между напряжением и током в цепи с емкостным сопротивлением в отсутствие активного сопротивления. б) Процесс перезарядки конденсатора в цепи переменного тока

Когда конденсатор заряжен до максимума (т. е. , а следовательно, иимеют максимальное значение), токи вся энергия цепи есть электрическая энергия заряженного конденсатора (точкана рис. 307,а). При уменьшении напряженияконденсатор начинает разряжаться и в цепи появляется ток; он направлен от обкладки 1 к обкладке 2, т. е. навстречу напряжению. Поэтому на рис. 307,а он изображен как отрицательный (точки лежат ниже оси времени). К моменту времениконденсатор полностью разряжен (и), а ток достигает максимального значения (точка); электрическая энергия равна нулю, и вся энергия сводится к энергии магнитного поля, создаваемого током. Далее, напряжениеменяет знак, и ток начинает ослабевать, сохраняя прежнее направление. Когда(и) достигнет максимума, вся энергия вновь станет электрической, и ток(точка). В дальнейшем(и) начинает убывать, конденсатор разряжается, ток нарастает, имея теперь направление от обкладки 2 к обкладке 1, т. е. положительное; ток доходит до максимума в момент, когда(точка) и т. д. Из рис. 307,а видно, что ток раньше, чем напряжение, достигает максимума и проходит через нуль, т. е. ток опережает напряжение по фазе.

Если активным сопротивлением цепи нельзя пренебречь по сравнению с емкостным, то ток опережает напряжение по времени меньше, чем на(сдвиг фаз меньше, рис. 308). Для этого случая, как показывает расчет, сдвиг фазможет быть вычислен по формуле

.               (162.2)

При имееми, как это объяснено выше.

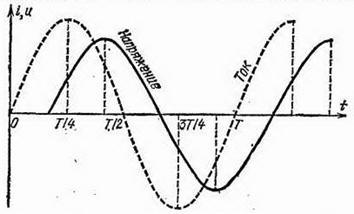
Рис. 308. Сдвиг фаз между током и напряжением в цепи, содержащей активное и емкостное сопротивления