
- •Тема 1 Методы и модели регрессионного анализа 7
- •Тема 2. Системы эконометрических уравнений 50
- •Тема 3. Анализ временных рядов 60
- •Предисловие
- •Введение. Эконометрическая модель и проблемы эконометрического моделирования
- •Общие понятия
- •Экономическая модель
- •Эконометрическая модель
- •Элементы эконометрической модели и их свойства
- •Задачи эконометрики
- •Эконометрика и её место в ряду математических и экономических дисциплин
- •Тема 1 Методы и модели регрессионного анализа
- •1.1 Основные понятия регрессионного анализа
- •1.1.1 Спецификация модели
- •1.2 Парная регрессия и корреляция
- •1.2.1 Линейная модель парной регрессии и корреляции
- •Оценка тесноты связи
- •Оценка качества подбора уравнения
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.2.2 Нелинейные модели парной регрессии и корреляции Виды нелинейных уравнений регрессии
- •Линеаризация нелинейных моделей регрессии
- •Оценка тесноты связи нелинейной регрессии
- •Оценка качества нелинейных уравнений регрессии
- •1.3 Множественная регрессия и корреляция
- •Отбор факторов, включаемых в модель множественной регрессии
- •1.3.1 Линейное уравнение множественной регрессии
- •Оценка параметров линейных уравнений регрессии
- •1.3.2 Линейное уравнение множественной регрессии с стандартизированном масштабе
- •1.3.2 Частные уравнения регрессии
- •1.3.3 Свойства оценок параметров эконометрической модели, получаемых при помощи мнк
- •1.3.4 Предпосылки мнк, методы их проверки
- •Обобщенный метод наименьших квадратов (омнк)
- •1.3.5 Проверка существенности факторов и показатели качества регрессии
- •Оценка тесноты связи
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.3.6 Фиктивные переменные во множественной регрессии
- •1.4 Резюме по теме.
- •Вопросы для повторения
- •Тема 2. Системы эконометрических уравнений
- •2.1. Классификация систем эконометрических уравнений
- •2.2 Структурная и приведенная формы модели
- •2.3 Проблема идентификации систем одновременных уравнений
- •2.4. Методы оценки параметров структурной формы модели (систем одновременных уравнений): косвенный метод наименьших квадратов (кмнк) и двухшаговый метод наименьших квадратов (дмнк)
- •2.5. Модель спроса и предложения
- •2.5.1 Структурная и приведённая форма системы
- •2.6. Вопросы для повторения
- •2.7. Резюме по теме
- •Тема 3. Анализ временных рядов
- •3.1. Структура временного ряда
- •3.2. Автокорреляция уровней временного ряда
- •Проверка гипотезы о наличии тренда во временном ряде
- •3.2. Моделирование тенденции временного ряда
- •3.3. Моделирование сезонных колебаний
- •3.3.1 Аддитивная и мультипликативная модели временных рядов
- •3.4. Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •3.5 Модели стационарных и нестационарных временных рядов и их идентификация
- •3.6 Эргодичность
- •3.7 Особые случаи
- •3.8 Нестационарные временные ряды
- •3.9 Метод разностей и интегрируемость
- •3.10 Адаптивные методы краткосрочного прогнозирования временных рядов
- •3.10.1 Понятие адаптивной модели
- •3.10.2 Экспоненциальное сглаживание
- •3.10.3 Модели линейного роста
- •3.10.4 Стохастический процесс Тейла и Вейджа
- •3.10.5 Сезонные модели
- •Аддитивная модель сезонных явлений
- •3.10.6 Модели авторегрессии — скользящего среднего (метод Бокса —Дженкинса)
- •3.10.7 Авторегрессионная модель.
- •3.10.8 Модель скользящего среднего.
- •3.11 Специфика изучения взаимосвязей по временным рядам. Исключение сезонных колебаний. Исключение тенденции.
- •3.11.1. Метод отклонений от тренда
- •3.11.2. Метод последовательных разностей
- •3.12 Резюме по теме.
- •3.13 Вопросы для повторения
1.2.1 Линейная модель парной регрессии и корреляции
Рассмотрим простейшую модель парной регрессии – линейную регрессию. Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
![]() или
или
![]() . (1.1)
. (1.1)
Уравнение вида
![]() позволяет по заданным значениям фактора
позволяет по заданным значениям фактора![]() находить теоретические значения
результативного признака, подставляя
в него фактические значения фактора
находить теоретические значения
результативного признака, подставляя
в него фактические значения фактора![]() .
.
Построение линейной
регрессии сводится к оценке ее параметров
–
![]() и
и![]() .
Классический подход к оцениванию
параметров линейной регрессии основан
наметоде наименьших квадратов(МНК). МНК позволяет получить такие
оценки параметров
.
Классический подход к оцениванию
параметров линейной регрессии основан
наметоде наименьших квадратов(МНК). МНК позволяет получить такие
оценки параметров![]() и
и![]() ,
при которых сумма квадратов отклонений
фактических значений результативного
признака
,
при которых сумма квадратов отклонений
фактических значений результативного
признака![]() от теоретических
от теоретических![]() минимальна:
минимальна:
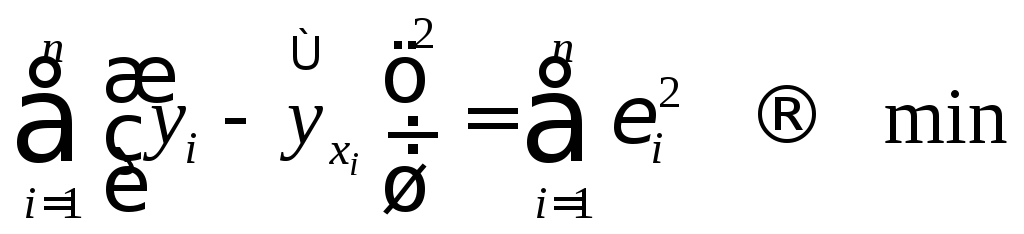 . (1.2)
. (1.2)
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):

Рис. 1.2.Линия регрессии с минимальной дисперсией остатков.
Как известно из
курса математического анализа, чтобы
найти минимум функции (1.2), надо вычислить
частные производные по каждому из
параметров
![]() и
и![]() и приравнять их к нулю. Обозначим
и приравнять их к нулю. Обозначим![]() через
через![]() ,
тогда:
,
тогда:![]() .
.
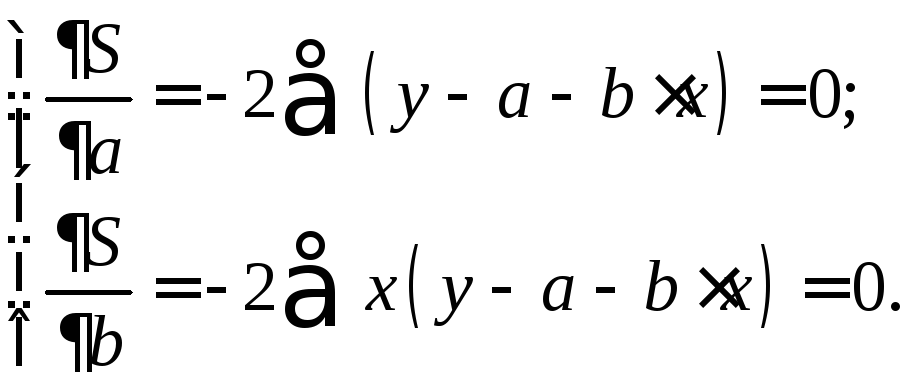 (1.3)
(1.3)
После несложных
преобразований, получим следующую
систему линейных уравнений для оценки
параметров
![]() и
и![]() :
:
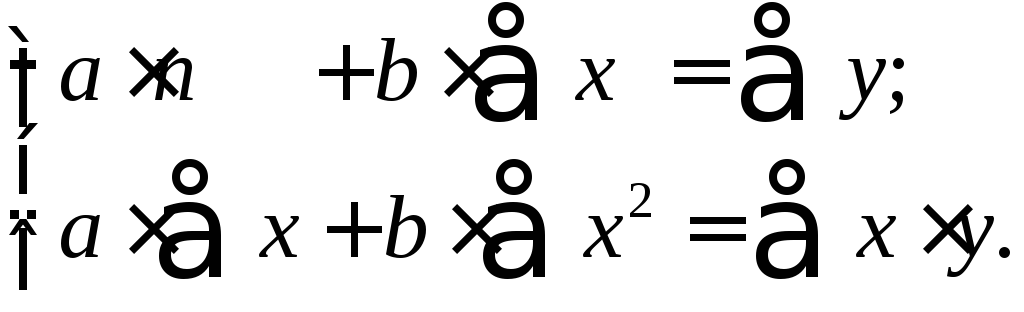 (1.4)
(1.4)
Решая систему
уравнений (1.4), найдем искомые оценки
параметров
![]() и
и![]() .
Можно воспользоваться следующими
готовыми формулами, которые следуют
непосредственно из решения системы
(1.4):
.
Можно воспользоваться следующими
готовыми формулами, которые следуют
непосредственно из решения системы
(1.4):
![]() ,
, ![]() , (1.5)
, (1.5)
где
![]() – ковариация признаков
– ковариация признаков![]() и
и![]() ,
,![]() – дисперсия признака
– дисперсия признака![]() и
и
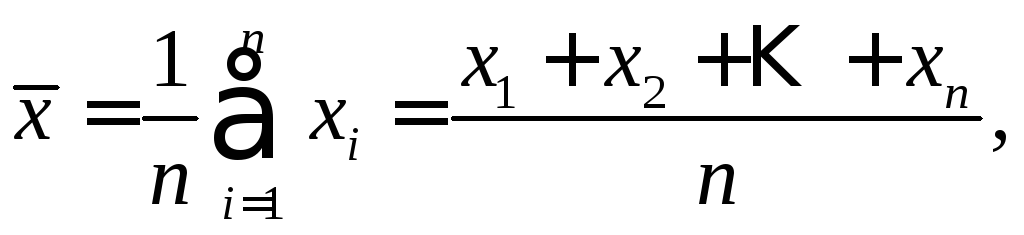
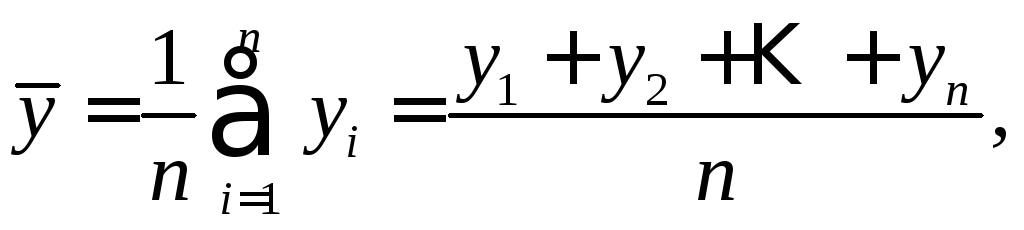
![]() ,
,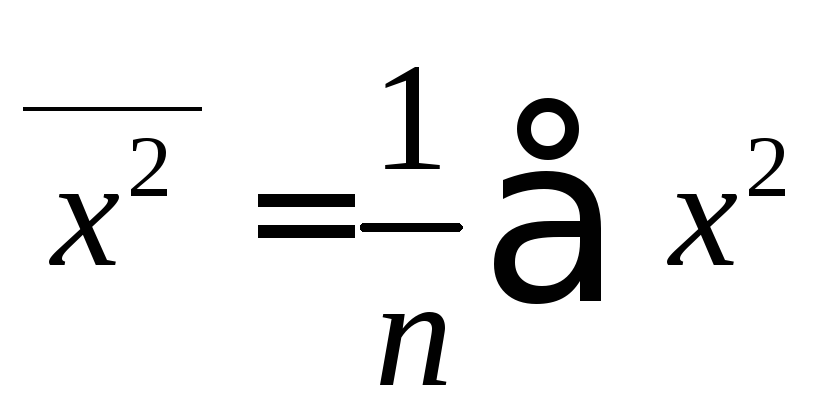
Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий. Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.
Параметр
![]() называетсякоэффициентом регрессии.
Его величина показывает среднее изменение
результата с изменением фактора на одну
единицу.
называетсякоэффициентом регрессии.
Его величина показывает среднее изменение
результата с изменением фактора на одну
единицу.
Формально
![]() – значение
– значение![]() при
при![]() .
Если признак-фактор
.
Если признак-фактор![]() не может иметь нулевого значения, то
вышеуказанная трактовка свободного
члена
не может иметь нулевого значения, то
вышеуказанная трактовка свободного
члена![]() не имеет смысла, т.е. параметр
не имеет смысла, т.е. параметр![]() может не иметь экономического содержания.
может не иметь экономического содержания.
Оценка тесноты связи
Уравнение регрессии
всегда дополняется показателем тесноты
связи. При использовании линейной
регрессии в качестве такого показателя
выступает линейный коэффициент
корреляции![]() ,
который можно рассчитать по следующим
формулам:
,
который можно рассчитать по следующим
формулам:
![]() (1.6)
(1.6)
Линейный коэффициент
корреляции находится в пределах:
![]() .
Чем ближе абсолютное значение
.
Чем ближе абсолютное значение![]() к единице, тем сильнее линейная связь
между факторами (при
к единице, тем сильнее линейная связь
между факторами (при![]() имеем строгую функциональную зависимость).
имеем строгую функциональную зависимость).
Теснота линейной связи между переменными может быть оценена на основании шкалы Чеддока:
|
Теснота связи |
Значение коэффициента корреляции при наличии: | |
|
Прямой связи |
Обратной связи | |
|
Слабая |
0,1–0,3 |
(–0,3)–(–0,1) |
|
Умеренная |
0,3–0,5 |
(–0,5)–(–0,3) |
|
Заметная |
0,5–0,7 |
(–0,7)–(–0,5) |
|
Высокая |
0,7–0,9 |
(–0,9)–(–0,7) |
|
Весьма высокая |
0,9–1 |
(–1)–(–0,9) |
Положительное значение коэффициента корреляции говорит о положительной связи между хиу, когда с ростом одной из переменных другая тоже растет. Отрицательное значение коэффициента корреляции означает, с ростом одной из переменных другая убывает, с убыванием одной из переменной другая растет.
