
- •Тема 1 Методы и модели регрессионного анализа 7
- •Тема 2. Системы эконометрических уравнений 50
- •Тема 3. Анализ временных рядов 60
- •Предисловие
- •Введение. Эконометрическая модель и проблемы эконометрического моделирования
- •Общие понятия
- •Экономическая модель
- •Эконометрическая модель
- •Элементы эконометрической модели и их свойства
- •Задачи эконометрики
- •Эконометрика и её место в ряду математических и экономических дисциплин
- •Тема 1 Методы и модели регрессионного анализа
- •1.1 Основные понятия регрессионного анализа
- •1.1.1 Спецификация модели
- •1.2 Парная регрессия и корреляция
- •1.2.1 Линейная модель парной регрессии и корреляции
- •Оценка тесноты связи
- •Оценка качества подбора уравнения
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.2.2 Нелинейные модели парной регрессии и корреляции Виды нелинейных уравнений регрессии
- •Линеаризация нелинейных моделей регрессии
- •Оценка тесноты связи нелинейной регрессии
- •Оценка качества нелинейных уравнений регрессии
- •1.3 Множественная регрессия и корреляция
- •Отбор факторов, включаемых в модель множественной регрессии
- •1.3.1 Линейное уравнение множественной регрессии
- •Оценка параметров линейных уравнений регрессии
- •1.3.2 Линейное уравнение множественной регрессии с стандартизированном масштабе
- •1.3.2 Частные уравнения регрессии
- •1.3.3 Свойства оценок параметров эконометрической модели, получаемых при помощи мнк
- •1.3.4 Предпосылки мнк, методы их проверки
- •Обобщенный метод наименьших квадратов (омнк)
- •1.3.5 Проверка существенности факторов и показатели качества регрессии
- •Оценка тесноты связи
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.3.6 Фиктивные переменные во множественной регрессии
- •1.4 Резюме по теме.
- •Вопросы для повторения
- •Тема 2. Системы эконометрических уравнений
- •2.1. Классификация систем эконометрических уравнений
- •2.2 Структурная и приведенная формы модели
- •2.3 Проблема идентификации систем одновременных уравнений
- •2.4. Методы оценки параметров структурной формы модели (систем одновременных уравнений): косвенный метод наименьших квадратов (кмнк) и двухшаговый метод наименьших квадратов (дмнк)
- •2.5. Модель спроса и предложения
- •2.5.1 Структурная и приведённая форма системы
- •2.6. Вопросы для повторения
- •2.7. Резюме по теме
- •Тема 3. Анализ временных рядов
- •3.1. Структура временного ряда
- •3.2. Автокорреляция уровней временного ряда
- •Проверка гипотезы о наличии тренда во временном ряде
- •3.2. Моделирование тенденции временного ряда
- •3.3. Моделирование сезонных колебаний
- •3.3.1 Аддитивная и мультипликативная модели временных рядов
- •3.4. Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •3.5 Модели стационарных и нестационарных временных рядов и их идентификация
- •3.6 Эргодичность
- •3.7 Особые случаи
- •3.8 Нестационарные временные ряды
- •3.9 Метод разностей и интегрируемость
- •3.10 Адаптивные методы краткосрочного прогнозирования временных рядов
- •3.10.1 Понятие адаптивной модели
- •3.10.2 Экспоненциальное сглаживание
- •3.10.3 Модели линейного роста
- •3.10.4 Стохастический процесс Тейла и Вейджа
- •3.10.5 Сезонные модели
- •Аддитивная модель сезонных явлений
- •3.10.6 Модели авторегрессии — скользящего среднего (метод Бокса —Дженкинса)
- •3.10.7 Авторегрессионная модель.
- •3.10.8 Модель скользящего среднего.
- •3.11 Специфика изучения взаимосвязей по временным рядам. Исключение сезонных колебаний. Исключение тенденции.
- •3.11.1. Метод отклонений от тренда
- •3.11.2. Метод последовательных разностей
- •3.12 Резюме по теме.
- •3.13 Вопросы для повторения
3.6 Эргодичность
Основная проблема в оценивании параметров распределения стохастического процесса состоит в том, что в общем случае размер выборки n = 1, поскольку обычно имеется единственная реализация процесса. Ввиду этого сделать осмысленную оценку практически невозможно. Изучаемый стохастический процесс как таковой неизвестен. Его стационарность или нестационарность может быть установлена только посредством анализа соответствующего ему временного ряда. Но, с другой стороны, многие методы анализа временных рядов предполагают их стационарность. Это приводит к своего рода замкнутому кругу, когда свойство, на наличие которого проводится исследование, входит в изначальные предпосылки.
Данную
проблему можно решить с использованием
понятия эргодичность:
это поведение большого класса стационарных
процессов, когда арифметическое среднее
со временем сходится к математическому
ожиданию μ. Эргодичность делает возможным
оценивание
![]() стохастического процесса только по его
реализации - временному ряду.
стохастического процесса только по его
реализации - временному ряду.
Известны различные подходы к распознаванию стационарности временных рядов:
графическое представление временного ряда и визуальная проверка на наличие какого-либо тренда, т.е. меняющегося среднего, увеличивающейся или уменьшающейся дисперсии, устойчивых периодичностей;
исследование на наличие автокорреляции в реальных данных;
тесты на присутствие детерминистического тренда, например t - тест на коэффициенты оценок метода наименьших квадратов;
тесты на наличие стохастического тренда, например тесты на единичный корень.
3.7 Особые случаи
Процесс называется нормальным, если совместное распределение Xt1 , Xt2 ,..., Xtn - это n-мерное нормальное распределение. В данном случае из стационарности в слабом смысле следует стационарность в сильном смысле.
«Белым шумом» называется чисто случайный процесс, т.е. ряд независимых, одинаково распределенных случайных величин at (iid). Главные свойства «белого шума» следующие:
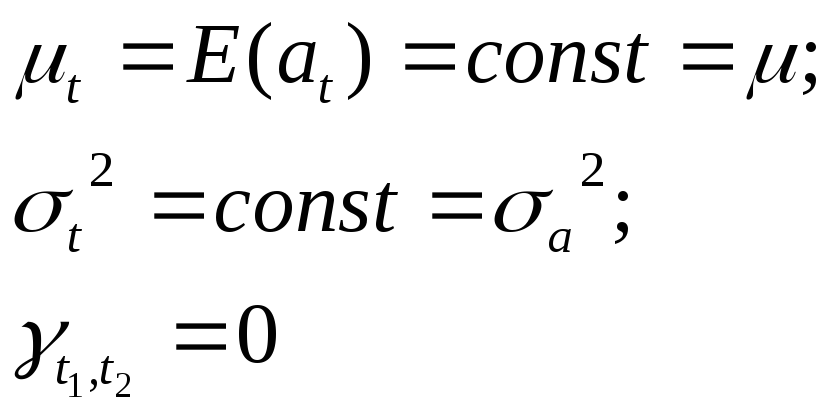
для
![]() .
.
Из этого очевидным образом следует стационарность. «Белый шум» играет важную роль при моделировании остатков или шоков стохастического процесса, генерирующего данные (временной ряд).
Для
того чтобы проверить, является ли
временной ряд xt
«белым шумом», можно протестировать
его выборочную автокорреляцию
![]() с
помощью Q-статистики Бокса - Пирса:
с
помощью Q-статистики Бокса - Пирса:
![]() .
.
При
нулевой гипотезе о том, что Xt
- «белый шум»
Q-статистика имеет
![]() -распределение
ср
степенями свободы.
-распределение
ср
степенями свободы.
3.8 Нестационарные временные ряды
Если временной ряд содержит, например, некоторый тренд, то требование постоянства дисперсии, среднего и ковариации нарушается, и мы имеем дело с нестационарным процессом, или процессом случайного блуждания. На практике временной ряд xtможно субъективно определить как нестационарный при помощи графика временного ряда и его коррелограмм. Если на них обнаруживаются:
1) тренд;
2) детерминистическая периодичность;
3) гетероскедастичность;
4) изменяющаяся автокорреляция,
то имеются веские причины предполагать, что лежащий в основе процесс является нестационарным. Теоретически он нестационарен, если среднее или дисперсия, или ковариация случайного процесса, сгенерировавшего этот временной ряд, изменяются во времени.
Как правило, временные ряды, характеризующие экономические явления, отличаются нестационарностью. Это связано с некоторыми свойствами экономических временных рядов, прежде всего с наличием тренда. Очевидно, что при наличии трендовой компоненты сложно утверждать, что среднее значение ряда, а также его дисперсия и автоковариация не зависят от времени, следовательно, ряд нестационарен. Временные ряды могут иметь как строго возрастающий (убывающий) тренд, так и заметные колебания на фоне общего тренда. Подобное поведение характерно для показателей ВВП, а также для показателей инфляции и процентной ставки.
Для некоторых нестационарных временных рядов характерно случайное блуждание. Обычно такие временные ряды не выказывают тенденции ни к возрастанию, ни к убыванию. Временной ряд может возрастать или убывать со временем и не сохранять среднего значения в долгосрочном периоде.
Еще одной из причин, вызывающих нестационарность временных рядов, является высокая инерционность внезапного воздействия (шока) на временной ряд. Во время экономического спада или бума основные макроэкономические показатели претерпевают сильные изменения и остаются на новом уровне в течение длительного промежутка времени, не возвращаясь к своему прежнему положению.
Относительно длинные временные ряды, характеризующие, например, процессы инфляции или уровень инвестиций, в некоторых случаях можно охарактеризовать как условно гетероскедастичные. Это означает, что в долгосрочном периоде (на протяжении нескольких десятков лет) дисперсия ряда постоянна, но в рамках данного периода имеются более короткие отрезки времени (продолжительностью в несколько лет), на протяжении которых дисперсия явления относительно высока.
Идентификация рядов, основанная на проверке постоянства среднего, дисперсии и ковариации, невозможна, так как априори структура ряда неизвестна.
Для получения критерия, который можно было бы использовать для выявления нестационарности рядов, рассмотрим авторегрессионный процесс Ytпервого порядка:
![]() .
(3.6)
.
(3.6)
Несложно проверить,
что при
![]() условия выполняются, а при
условия выполняются, а при![]() -
не выполняются, т.е. в первом случае
можно говорить о стационарном, а во
втором случае - о нестационарном процессе
yt, поэтому нестационарные процессы
называют также процессами единичного
корня.
-
не выполняются, т.е. в первом случае
можно говорить о стационарном, а во
втором случае - о нестационарном процессе
yt, поэтому нестационарные процессы
называют также процессами единичного
корня.
Между стационарными и нестационарными временными рядами имеется существенное отличие. Единовременное шоковое воздействие на стационарный ряд носит временный характер. Со временем эффект рассеивается, и значения временного ряда возвращаются к своему долгосрочному среднему значению. Следовательно, долгосрочный прогноз стационарного ряда сходится к безусловному среднему. Для облегчения идентификации стационарных рядов будем использовать следующие свойства:
Уровни ряда колеблются вокруг постоянного долгосрочного среднего значения.
Временной ряд имеет постоянную, не зависящую от времени дисперсию.
Временной ряд имеет теоретическую коррелограмму, которая убывает при возрастании длины лага.
С другой стороны, нестационарные ряды обязательно имеют постоянную компоненту, среднее и/или дисперсия зависят от времени. Перечисленные ниже свойства помогут идентифицировать нестационарные временные ряды.
В долгосрочном периоде не существует постоянного среднего значения, к которому возвращаются значения временного ряда.
Дисперсия зависит от времени и по мере увеличения времени растет до бесконечности.
Теоретическая автокорреляция не сокращается, но для наблюдений, ограниченных некоторыми пределами, медленно затухает.
Для формального определения стационарности ряда эти свойства не подходят. В основу тестов на идентификацию временных рядов положена проверка условия равенства или неравенства параметра α1 из уравнения (10.1) единице. Это так называемые тесты единичного корня.
