- •Тема 1 Методы и модели регрессионного анализа 7
- •Тема 2. Системы эконометрических уравнений 50
- •Тема 3. Анализ временных рядов 60
- •Предисловие
- •Введение. Эконометрическая модель и проблемы эконометрического моделирования
- •Общие понятия
- •Экономическая модель
- •Эконометрическая модель
- •Элементы эконометрической модели и их свойства
- •Задачи эконометрики
- •Эконометрика и её место в ряду математических и экономических дисциплин
- •Тема 1 Методы и модели регрессионного анализа
- •1.1 Основные понятия регрессионного анализа
- •1.1.1 Спецификация модели
- •1.2 Парная регрессия и корреляция
- •1.2.1 Линейная модель парной регрессии и корреляции
- •Оценка тесноты связи
- •Оценка качества подбора уравнения
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.2.2 Нелинейные модели парной регрессии и корреляции Виды нелинейных уравнений регрессии
- •Линеаризация нелинейных моделей регрессии
- •Оценка тесноты связи нелинейной регрессии
- •Оценка качества нелинейных уравнений регрессии
- •1.3 Множественная регрессия и корреляция
- •Отбор факторов, включаемых в модель множественной регрессии
- •1.3.1 Линейное уравнение множественной регрессии
- •Оценка параметров линейных уравнений регрессии
- •1.3.2 Линейное уравнение множественной регрессии с стандартизированном масштабе
- •1.3.2 Частные уравнения регрессии
- •1.3.3 Свойства оценок параметров эконометрической модели, получаемых при помощи мнк
- •1.3.4 Предпосылки мнк, методы их проверки
- •Обобщенный метод наименьших квадратов (омнк)
- •1.3.5 Проверка существенности факторов и показатели качества регрессии
- •Оценка тесноты связи
- •Проверка статистической значимости эконометрической модели
- •Оценка значимости параметров эконометрической модели
- •1.3.6 Фиктивные переменные во множественной регрессии
- •1.4 Резюме по теме.
- •Вопросы для повторения
- •Тема 2. Системы эконометрических уравнений
- •2.1. Классификация систем эконометрических уравнений
- •2.2 Структурная и приведенная формы модели
- •2.3 Проблема идентификации систем одновременных уравнений
- •2.4. Методы оценки параметров структурной формы модели (систем одновременных уравнений): косвенный метод наименьших квадратов (кмнк) и двухшаговый метод наименьших квадратов (дмнк)
- •2.5. Модель спроса и предложения
- •2.5.1 Структурная и приведённая форма системы
- •2.6. Вопросы для повторения
- •2.7. Резюме по теме
- •Тема 3. Анализ временных рядов
- •3.1. Структура временного ряда
- •3.2. Автокорреляция уровней временного ряда
- •Проверка гипотезы о наличии тренда во временном ряде
- •3.2. Моделирование тенденции временного ряда
- •3.3. Моделирование сезонных колебаний
- •3.3.1 Аддитивная и мультипликативная модели временных рядов
- •3.4. Автокорреляция в остатках. Критерий Дарбина-Уотсона
- •3.5 Модели стационарных и нестационарных временных рядов и их идентификация
- •3.6 Эргодичность
- •3.7 Особые случаи
- •3.8 Нестационарные временные ряды
- •3.9 Метод разностей и интегрируемость
- •3.10 Адаптивные методы краткосрочного прогнозирования временных рядов
- •3.10.1 Понятие адаптивной модели
- •3.10.2 Экспоненциальное сглаживание
- •3.10.3 Модели линейного роста
- •3.10.4 Стохастический процесс Тейла и Вейджа
- •3.10.5 Сезонные модели
- •Аддитивная модель сезонных явлений
- •3.10.6 Модели авторегрессии — скользящего среднего (метод Бокса —Дженкинса)
- •3.10.7 Авторегрессионная модель.
- •3.10.8 Модель скользящего среднего.
- •3.11 Специфика изучения взаимосвязей по временным рядам. Исключение сезонных колебаний. Исключение тенденции.
- •3.11.1. Метод отклонений от тренда
- •3.11.2. Метод последовательных разностей
- •3.12 Резюме по теме.
- •3.13 Вопросы для повторения
3.2. Автокорреляция уровней временного ряда
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Формула для расчета коэффициента автокорреляции имеет вид:
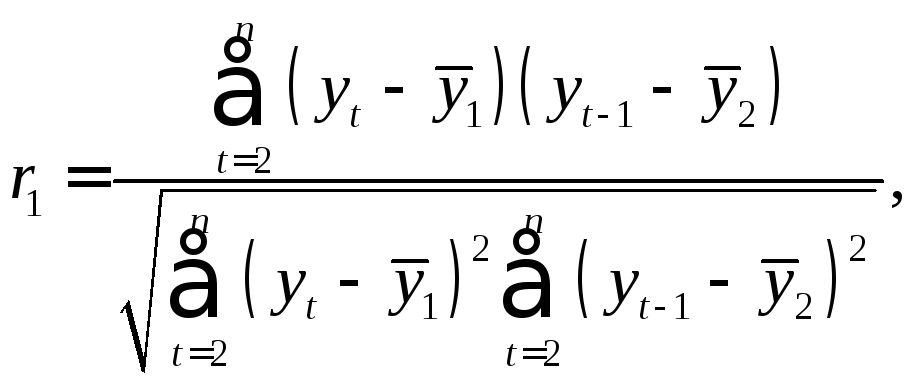 (3.1)
(3.1)
где
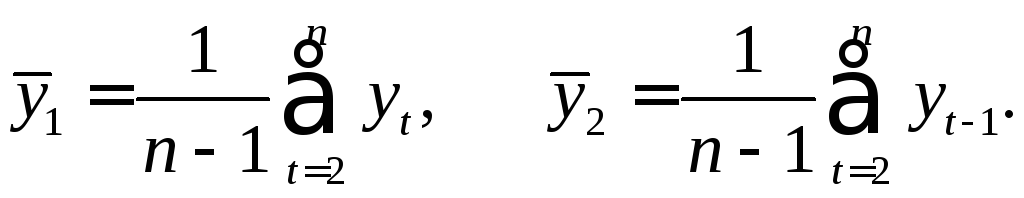
Эту величину
называют коэффициентом автокорреляцииуровней ряда первого порядка, так как
он измеряет зависимость между соседними
уровнями ряда![]() и
и![]() .
.
Аналогично можно
определить коэффициенты автокорреляции
второго и более высоких порядков. Так,
коэффициент автокорреляции второго
порядка характеризует тесноту связи
между уровнями
![]() и
и![]() и определяется по формуле:
и определяется по формуле:
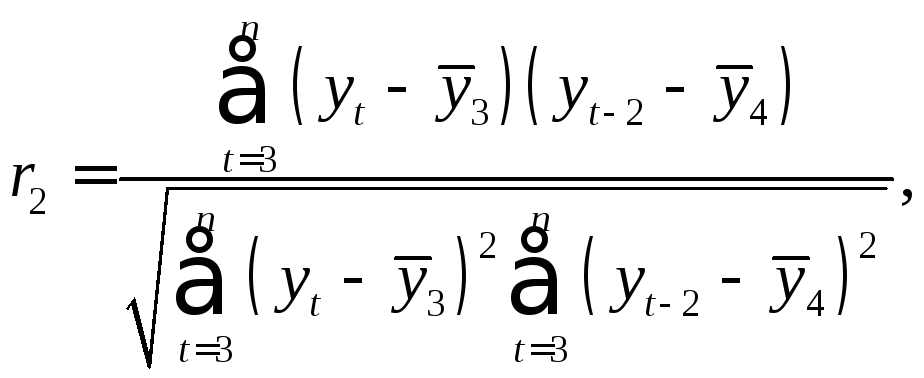 (3.2)
(3.2)
где
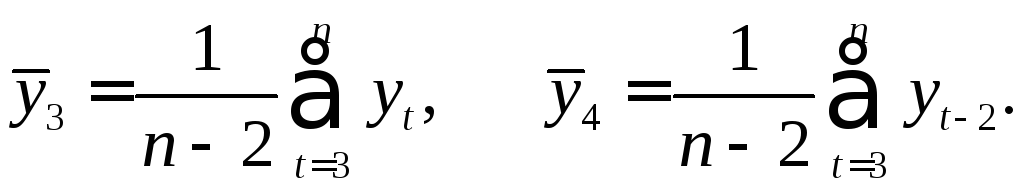
Если наиболее
высоким оказался коэффициент автокорреляции
первого порядка, исследуемый ряд содержит
только тенденцию. Если наиболее высоким
оказался коэффициент автокорреляции
порядка
![]() ,
то ряд содержит циклические колебания
с периодичностью в
,
то ряд содержит циклические колебания
с периодичностью в![]() моментов времени. Если ни один из
коэффициентов автокорреляции не является
значимым, можно сделать одно из двух
предположений относительно структуры
этого ряда: либо ряд не содержит тенденции
и циклических колебаний, либо ряд
содержит сильную нелинейную тенденцию,
для выявления которой нужно провести
дополнительный анализ.
моментов времени. Если ни один из
коэффициентов автокорреляции не является
значимым, можно сделать одно из двух
предположений относительно структуры
этого ряда: либо ряд не содержит тенденции
и циклических колебаний, либо ряд
содержит сильную нелинейную тенденцию,
для выявления которой нужно провести
дополнительный анализ.
Свойства коэффициента автокорреляции.
Он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции.
По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функциейвременного ряда. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называетсякоррелограммой.
Проверка гипотезы о наличии тренда во временном ряде
Даны значения временного ряда x(1), x(2),..., x(n).Необходимо определить, имеет ли этот ряд неслучайную компоненту, зависящую от времени - тренд.
Пусть xmed - выборочная медиана этого временного ряда. Образуем рядz(1), z(2),..., z(n) следующим образом:
z(i) = знак(x(i) - xmed).
Серия - это группа подряд идущих +1 или -1.
Обозначим (n) -количество серий;(n) - длина самой протяжённой серии.
Критерий, основанный на выборочной медиане состоит в следующем:
если выполняются оба неравенства
![]()
![]()
тогда с вероятностью, заключённой между 0,9025 и 0,95 делается вывод о неизменности среднего значения ряда и об отсутствии тренда. Если хотя бы одно из неравенств не выполняется, тогда с такой же вероятностью следует сделать вывод о наличии тренда.
Алгоритм скользящего среднего заключается в следующем:
![]()
![]()
где wk– некоторые весовые коэффициенты, в сумме равные 1, т.е.
![]()
Для 2m+1 элементов временного рядаx(1),x(2),…,x(2m+1) строится полином степениpметодом наименьших квадратов
значение этого
полинома используют для расчёта значений
оценки тренда
![]() в
средней точке этого отрезка рядаm+ 1, т.е.
в
средней точке этого отрезка рядаm+ 1, т.е.
![]()
Эта же процедура выполняется для отрезка временного ряда x(2),…,x(2m+2).
Эта идея реализована в методе экспоненциально взвешенного скользящего среднего Брауна
![]()
![]()
Дисперсия остаточной случайной компоненты после сглаживания
![]()
где
![]() –остаточная
нерегулярная компонента после сглаживания.
–остаточная
нерегулярная компонента после сглаживания.
2=Dx(t);
поэтому при
значениях , не
слишком близких к 1, и для достаточно
удалённых от прошлого значенийtслучайные остатки![]() подвержены
существенно меньшему разбросу.
подвержены
существенно меньшему разбросу.
Рекуррентный
способ вычисления сглаженных значений
![]() .
.
![]() ;
;
![]()
![]()
![]()
![]()
![]()
Среднее значение
М(t) = a;
дисперсия
D(t) = M((t) – a)2 = 2.
Оценки
![]()
![]()
Так как значения временного ряда в моменты времени t,t+являются случайными величинами, можно рассмотреть коэффициент корреляции между ними…
![]()
Корреляционной функцией стационарного временного ряда называется функция
![]()
для стационарного временного ряда
D(t) =D(t+) =2,
поэтому
![]()
таким образом, корреляционная функция в точке – это коэффициент корреляции между значениями ряда, отстоящими друг от друга на временной промежуток.
Оценка корреляционной функции
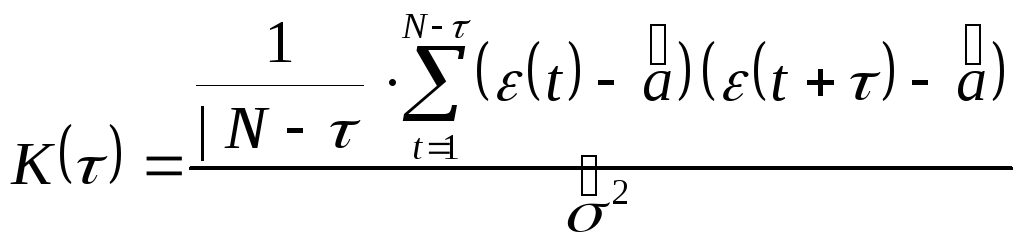
при сильной
положительной зависимости (t),(t+)
в числителе будет много положительных
слагаемых, и корреляционная функция
будет иметь большое положительное
значение; при сильной отрицательной
зависимости (при(t)
>![]() с большой вероятностью(t)
<
с большой вероятностью(t)
<![]() )
в числителе будет много отрицательных
слагаемых, и корреляционная функция
будет иметь малое отрицательное значение;
при слабой зависимости(t),(t+)
примерно одинаковое количество слагаемых
будут иметь положительные и отрицательные
знаки, в это случае корреляционная
функция будет мала по абсолютной
величине.
)
в числителе будет много отрицательных
слагаемых, и корреляционная функция
будет иметь малое отрицательное значение;
при слабой зависимости(t),(t+)
примерно одинаковое количество слагаемых
будут иметь положительные и отрицательные
знаки, в это случае корреляционная
функция будет мала по абсолютной
величине.
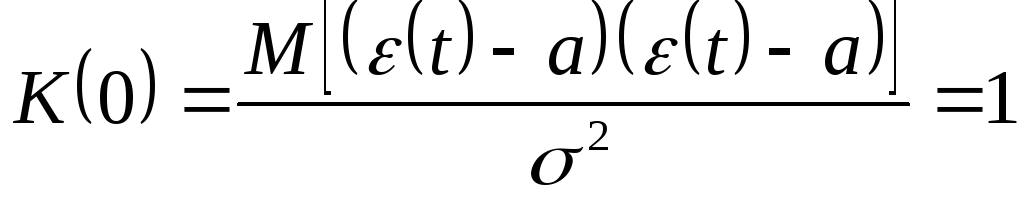 ,
что очевидно должно быть, так как
измеряется коэффициент корреляции
между одинаковыми случайными величинами.
,
что очевидно должно быть, так как
измеряется коэффициент корреляции
между одинаковыми случайными величинами.Чем больше , т.е. сильнее разнесены во времени значения временного ряда (t), (t+), тем слабее взаимосвязь между этими значениями, тем должна быть меньше по абсолютной величине K(). Поэтому K() 0 при .
|K()|1.
Для марковских процессов доказано, что
1) M(t) = 0,
2) K() =,
Таким образом, большое положительное (близкое к 1) значение означает сильную коррелированность значений временного ряда, отстоящих на небольшое значение , и медленное затухание этой зависимости с ростом . Временной ряд при таких имеет более плавный характер. При малом значении степень зависимости значений временного ряда быстро уменьшается. При этом ряд имеет более изрезанный «дёрганный характер».
K(1) = ,
то есть величина – это коэффициент корреляции соседних значений временного ряда.
3)
![]()
Из последнего соотношения следует, что, если значение || близко к 1, тогда дисперсия(t) будет значительно больше дисперсии возмущения(t). То есть, если соседние значения ряда(t) сильно коррелированны, то ряд довольно слабых возмущений(t) будет порождать размашистые колебания остатков(t).
Из соотношения
K(1) =,
следует способ идентификации модели авторегрессии 1-го порядка.
Оценка величины формируется как оценка корреляционной функции в точке 1: