
Дискретная математика / Графы
.docТеория графов
Основные положения
Теория графов — тот редкий раздел математики, о котором доподлинно известно, когда он родился и кто был его основоположником. Родилась теория графов в Санкт-Петербурге. Ее создателем является Л. Эйлер, который в 1736 году опубликовал решение задачи о Кенигсбергских мостах. Суть задачи состоит в следующем. Город Кенигсберг был построен в месте слияния двух рек на их берегах и на двух островах. В нем было семь мостов, которые соединяли острова между собой и с береговыми частями города. Мог ли любой житель города выйти из дома, пройти по всем семи мостам в точности по одному разу и вернуться домой?
На рис. 1 плана города a, b, c, d — части суши. Эйлер дал отрицательный ответ на поставленный вопрос. Более того, он доказал, что подобный маршрут имеется только для такого графа, каждая из вершин которого связана с четным числом ребер (на графе, изображенном на рисунке справа, части суши изображены точками — вершинами графа, а связи между ними - линиями произвольной конфигурации, называемыми ребрами или дугами).

Рис. 1. План города Кенигсберга и граф к задаче о Кенигсбергских мостах
Теорию графов начали разрабатывать
для решения некоторых задач о
геометрических конфигурациях,
состоящих из точек и линий. В этих задачах
несущественно, соединены ли точки
конфигурации отрезками прямых или
криволинейными дугами, какова длина
линий и другие геометрические
характеристики конфигурации. Важно
лишь то, что каждая линия соединяет
какие-либо две из заданных точек. Таким
образом, можно дать определение графа
как совокупности двух множеств V
(точек) и U (линий), между элементами
которых определено отношение инцидентности,
причем каждый элемент u![]() U
инцидентен ровно двум элементам v', v''.
Элементы множества V называются вершинами
графа G, элементы множества U — его
ребрами. Вершины и ребра графа G называют
еще его элементами и вместо v
U
инцидентен ровно двум элементам v', v''.
Элементы множества V называются вершинами
графа G, элементы множества U — его
ребрами. Вершины и ребра графа G называют
еще его элементами и вместо v![]() V,
u
V,
u![]() U
пишут соответственно v
U
пишут соответственно v
![]() G
и u
G
и u![]() G.
G.
Если две вершины соединены ребром, то говорят, что каждая вершина инцидентна этому ребру, а соответствующие вершины — смежны (две вершины, инцидентные одному ребру, - смежны). Два ребра, инцидентные одной вершине, также смежны.
В некоторых задачах инцидентные ребру вершины неравноправны, они рассматриваются в определенном порядке. Тогда каждому ребру можно приписать направление от первой из инцидентных вершин ко второй. Направленные ребра часто называют дугами, а содержащий их граф — ориентированным (граф, определенный ранее, называется неориентированным). Первая по порядку вершина, инцидентная ребру ориентированного графа, называется его началом, вторая — его концом. Говорят еще, что ребро ориентированного графа выходит из начала и входит в конец.
Понятие графа можно применить не только при исследовании геометрических конфигураций. Особенно часто определяют графы при анализе функционирования систем. С отдельными компонентами изучаемой системы удобно связывать вершины графа, а с парами взаимодействующих компонент — его ребра. Построенный таким образом граф называют структурным графом системы.
На рис.2,а – з изображены некоторые неориентированные графы. Множество ребер U может быть пустым (рис. 2,г). Если же множество вершин V пусто, то пусто и U. Такой граф называется пустым. Линии, изображающие ребра графа, могут пересекаться, но точки пересечения не являются вершинами (рис.1,д); различные ребра могут быть инцидентны одной и той же паре вершин (рис. 2, е), в этом случае они называются кратными; граф, содержащий кратные ребра, часто называют мультиграфом. Ребро может соединять некоторую вершину саму с собой (рис. 2,ж), такое ребро называется петлей. На рис. 2,з изображен фрагмент бесконечного графа. Его вершины — это точки плоскости с целыми координатами (х, у), а ребра — соединяющие их горизонтальные и вертикальные отрезки длины 1.
Обычно рассматриваемые графы конечны, т. е. конечны множества их элементов (вершин и ребер).

Рис. 2
При изображении ориентированных графов (рис. 3, а - з) направления ребер отмечаются стрелками, примыкающими к их концам. Ориентированный граф также может иметь кратные ребра (рис.3, е), петли (рис.3, ж), а также соединяющие одни и те же вершины ребра, идущие в противоположных направлениях (рис. 3, з).

Рис. 3
Степенью вершины называется число дуг, инцидентных ей. Вершина степени 1 называется висячей(рис. 3, ж, в). Вершина степени 0 называется изолированной(рис. 3, б).
Маршрутом в G называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют общую инцидентную вершину. Одно и то же ребро может встречаться в маршруте несколько раз.
Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а замкнутая простая цепь — простым циклом (рис. 4).

Рис. 4. Пример цепей и циклов в графе: (l2, l5, l6) - цепь; (l1, l2, l5) - простая цепь; (l2, l3, l4, l5) - цикл; (l2, l4, l5) - простой цикл.
Цикл, который содержит все ребра графа, называется эйлеровым циклом (соответствующей граф называется эйлеровым). Простой цикл, который проходит через все вершины графа, называется гамильтоновым.
Для ориентированных графов все введенные понятия сохраняются с заменой терминов маршрут на путь, а цикл на контур.
Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направления. Такое соответствие будем называть каноническим.
Подграфом Gа графа G = < V, U > называется граф, в который входит лишь часть вершин графа G, образующих множество А, вместе с ребрами (дугами), их соединяющими. Так, карта шоссейных дорог Пермской области является подграфом графа «Карта шоссейных дорог Российской Федерации».
Частичным графом Gа по отношению к графу G называется граф, содержащий только часть ребер (дуг) графа G. Так, карта главных дорог России - частичный граф карты шоссейных дорог России.
Граф связен, если любые две его вершины можно соединить цепью. Если граф не связен, то его можно разбить на отдельные связные подграфы, которые называются компонентами связности. Связный граф, не имеющий циклов (ациклический), называется деревом (рис. 5).

Рис.5. Граф – дерево
Деревом может быть задано отношение подчинения в трудовом коллективе, в государстве.
Простейшее дерево состоит из двух вершин, соединенных ребром. Каждый раз, когда добавляется еще одно ребро, в конце его прибавляется также и вершина. Следовательно, дерево с n вершинами имеет n - 1 ребро.
В теории графов доказывается, что число различных деревьев, которые можно построить на m вершинах, равно mm-2. Много деревьев — это лес.
Цикломатическое число. Пусть G - неориентированный связный граф, имеющий n вершин и m ребер. Цикломатическим числом связного графа G с n вершинами и m ребрами называется число:
ν(G) = m - n + 1.
Это число имеет интересный физический смысл: оно равно наибольшему числу независимых циклов в графе. При расчете электрических цепей цикломатическое число используется для определения числа независимых контуров.
Рассмотрим примеры подсчета числа независимых циклов.
В графе, состоящем из одной вершины и одного ребра, один цикл (рис. 6, а).
В графе, состоящем из одной вершины и трех ребер, три цикла (рис. 6, б).
В графе, состоящем из двух вершин и двух ребер, один цикл (рис. 6, в).
В графе, состоящем из двух вершин и пяти ребер, четыре цикла (рис. 6, г).
В графе, состоящем из трех вершин и трех ребер, один цикл (рис. 6, д).
В графе, состоящем из трех вершин и четырех ребер, два цикла (рис. 6, е).
В графе, состоящем из четырех вершин и четырех ребер, один цикл (рис. 6, ж).
В графе, состоящем из четырех вершин и пяти ребер, два цикла (рис. 6, з).
В графе, состоящем из четырех вершин и шести ребер, три цикла (рис. 6, и).
Цикломатическое число дерева равно нулю.

Рис.6. Примеры циклов в графах:
а, в, д, ж — один цикл; б, и - три цикла; г — четыре цикла; е, з — два цикла
Хроматическое число графа. Граф G называют р-хроматическим, где р - натуральное число, если его вершины можно раскрасить р-различными цветами так, чтобы никакие две смежные вершины не были раскрашены одинаково. Наименьшее число р, при котором граф является р-хроматическим, называют хроматическим числом графа и обозначают λ(G). Если λ (G) = 2, то граф называют бихроматическим. Необходимым и достаточным условием бихроматичности является отсутствие в графе циклов нечетной длины.
Граф на рис. 7, а — бихроматический, его вершины «раскрашены» двумя «цветами», обозначенными 0,1.
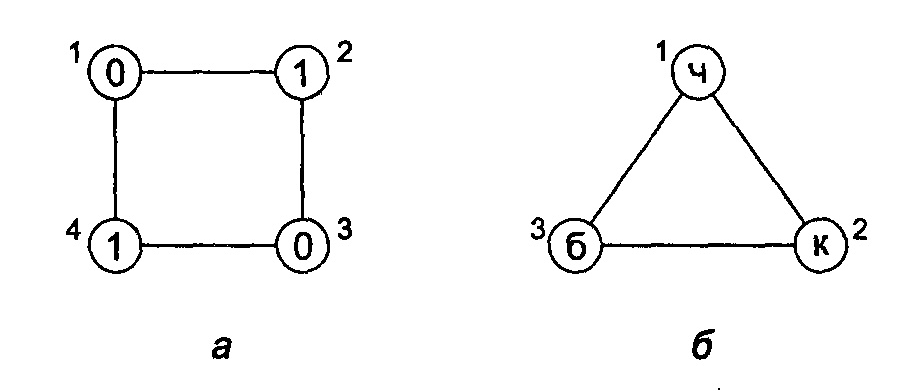
Рис. 7. Примеры раскраски графов: а - бихроматический граф; б - граф, раскрашенный тремя цветами
Граф на рис. 7, б можно «раскрасить» тремя цветами, например, черным (ч), красным (к) и белым (б).
Представления графов. Наиболее известный и популярный способ представления графов состоит в геометрическом изображении точек (вершин) и линий (ребер) на бумаге. При численном решении задач на вычислительных машинах граф должен быть представлен дискретным способом. Существует довольно много способов такого рода представления графов. Однако простота использования представления графа, как и эффективность алгоритма, в основе которого он лежит, в полной мере зависит от конкретного выбора этого представления. Одно из направлений теории графов связано с их матричным представлением. Существуют различные виды матриц, ассоциированные с графами. Эти алгебраические формы используются для решения многих задач теории графов. Рассмотрим две такие матричные формы:
1. Матрица смежности графа.
Матрицей смежности ориентированного помеченного графа с n вершинами называется матрица А= [aij], где i, j= 1, 2,..., n, в которой aij = 1, если существует ребро (хi, ,хj) или 0, если вершины хi, ,хj не связаны ребром (хi, ,хj).
Матрица смежности однозначно определяет структуру графа. Примеры орграфа и его матрицы смежности приведены соответственно на рис. 8 и рис. 9. Отметим, что петля в матрице смежности может быть представлена соответствующим единичным диагональным элементом. Кратные ребра можно представить, позволив элементу матрицы быть больше 1, но это не принято, обычно же представляют каждый элемент матрицы одним двоичным разрядом.

Рис. 8. Ориентированный граф

Рис.9. Матрица смежности ориентированного графа рис.8
Матрица инцидентности графа. Матрицей инцидентности для неориентированного графа с n вершинами и m ребрами называется матрица В= [bij], i = 1, 2,...,n, j= 1, 2…m, строки которой соответствуют вершинам, а столбцы — ребрам. Элементы bij = 1, если вершина хi, инцидентна ребру uj или bij = 0, если вершина xi не инцидентна ребру uj.
Пример графа и его матрицы инцидентности с 5 вершинами и 7 ребрами представлен на рис. 10 и рис.11 соответственно.

Рис.10. Ориентированный граф

Рис. 11. Матрица инцидентности графа рис.10
Список ребер графа. При описании графа списком его ребер каждое ребро представляется парой инцидентных ему вершин. Это представление можно реализовать двумя массивами r= (r1, r2, ..., rm) и t= (t1, t2, ..., tm), где m - количество ребер в графе. Каждый элемент в массиве есть метка вершины, а i-е ребро графа выходит из вершины ri, и входит в вершину ti. Например, соответствующие массивы представления графа на рис. 8 будут иметь вид:
r = (1, 1, 2, 2, 2, 2, 2, 3, 4, 4, 4, 6, 6, 6, 7, 7),
t = (2, 3, 1, 3, 4, 5, 7, 5, 1, 5, 7, 4, 5, 7, 4, 5).
