25. Табличный метод получения математических моделей систем

В табличном методе в вектор базисных координат получаются переменные величины типа U и I для всех ветвей схемы. Выбор такого базиса позволяет в эквива-1тной схеме иметь любые зависимые ветви. Из обобщенного метода табличный получается алгебраизацией компонентных уравнений, т. е. из вектора неизвестных, исключаются производные переменных состояния.

Представление компонентных уравнений удобно для формирования матрицы Якоби. Матри­ца Якоби, получаемая при использовании табличного метода, сильно разреженная. Чем меньше число ненуле­вых элементов в матрице, тем выше экономичность моде­ли, поэтому следует стремиться получить максимальную разреженность матрицы.

Поскольку структура компонентных уравнений опре­делена набором элементов, используемых в объекте, то влиять на разреженность можно только за счет тополо­гической части ММС. Один из алгоритмов, обеспечива­ющий высокую разреженность М-матрицы, а потому и разреженность топологической части матрицы Якоби, основан на включении в дерево в первую очередь тех ветвей (по возможности), которые обладают наиболь­шим весом. Вес ветви определяется суммарной кратно­стью вершин, между которыми она включена. Кратность вершины, в свою очередь, определяется количеством ветвей, ей инцидентных. Для графа гидромеханической системы ветви, включенные в дерево, отве­чают этому условию.

В общем виде алгебраизованная и линеаризованная система уравнений, получаемая табличным методом, мо-сет быть записана следующим образом:

26. Узловой метод получения математических моделей систем.

Узловой метод является популярным при создании программных комплексов анализа динамических систем. В качестве вектора базисных координат в этом методе используется вектор переменных типа узловых потенциалов, в качестве топологических уравнений - уравнения типа первого закона Кирхгофа. (7), где- вектор переменных, величин типа потенциала, характеризующих состояние узла (скорости, давления, температуры);I - вектор переменных величин типа потока (токи, силы, расходы, тепловые потоки). Топологические уравнения типа (7) могут быть получены с помощью матрицы инциденций А: (8) Из уравнений обобщенного метода получения топологических уравнений уравнение (8) может быть выведено следующим образом. В эквивалентную схему объекта вводятся фиктивные ветви, связывающие все узлы схемы с базовым (базовым может быть любой узел эквивалентной схемы; как правило, это узел, к которому подключено наибольшее количество ветвей). Проводимости этих ветвей равны нулю, т. е. переменная типаI в этих ветвях равна нулю.

28. Метод вращения Якоби

Метод применяется для решения стандартной задачи на собственные значения. Для начала введем понятия малой и большой задачи:

• малая задача - это когда матрица решаемой задачи располагается целиком во внешней памяти;

• большие задачи обычно распадаются на малые, которые решаются стандартно.

Рассматриваем малую задачу.

- Стандартная задача на собственные значения.

где

- известная матрица

- матрица поворота

- собственные числа матрицы А

Суть метода Якоби:

Метод Якоби заключается в том, чтобы подобрать матрицу Q, удовлетворяющую уравнению (2). Из условия ортогональности (1) следует:

Реализация:

В зависимости от угла делаем величины внедиагональных элементов матрицы А как можно меньше:

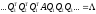
Если внедиагональные элементы стали меньше заданного числа, то можно считать, что задача решена с определенной степенью точности.

Также отметим, что: