Лекция 7. Многофакторные эколого-математические модели. Анализ влияния отдельных факторов в экологической модели.

В практике часто возникают ситуации, когда функция отклика (цели) У зависит не от одного, а от многих факторов. Установление формы связи в этих случаях начинают, как правило, с рассмотрения линейной регрессии вида

В этом случае результаты наблюдений должны быть представлены

уравнениями, полученными в каждом из и опытов:

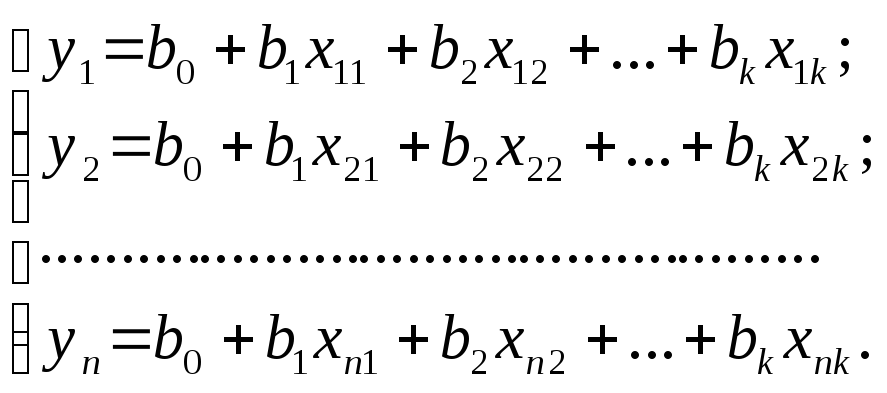
или в виде матрицы результатов наблюдений

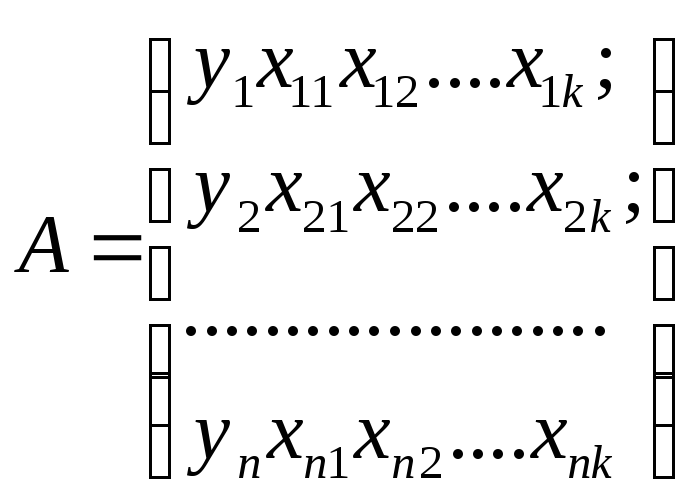
где n — количество опытов; k — количество факторов.

Для решения систем уравнений необходимо, чтобы количество опытов было не менее (k+1), т.е. n > k+l.

Задачей множественного регрессионного анализа является пост- роение такого уравнения прямой в k-мерном пространстве, откло- нения результатов наблюдений х_ij от которой были бы минималь- ными. Используя для этого метод наименьших квадратов, получаем систему нормальных уравнений

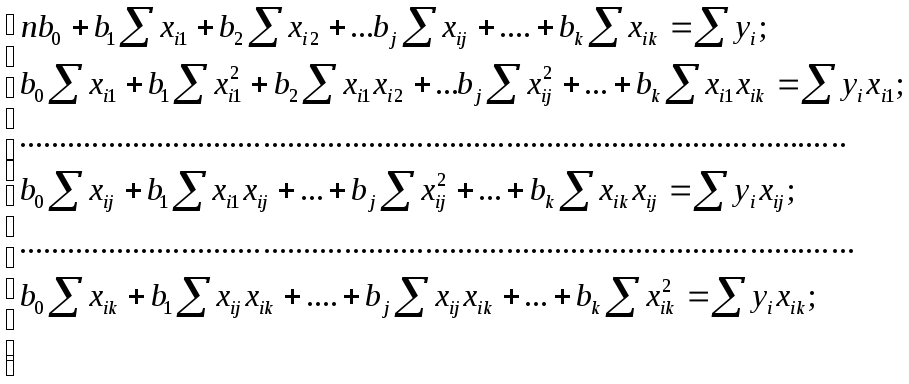
В матричном виде

,

где В — вектор-столбец коэффициентов уравнения регрессии;

Х — матрица значений факторов; Y — вектор-столбец функций отклика; Х^T — транспонированная матрица Х Они соответственно равны:

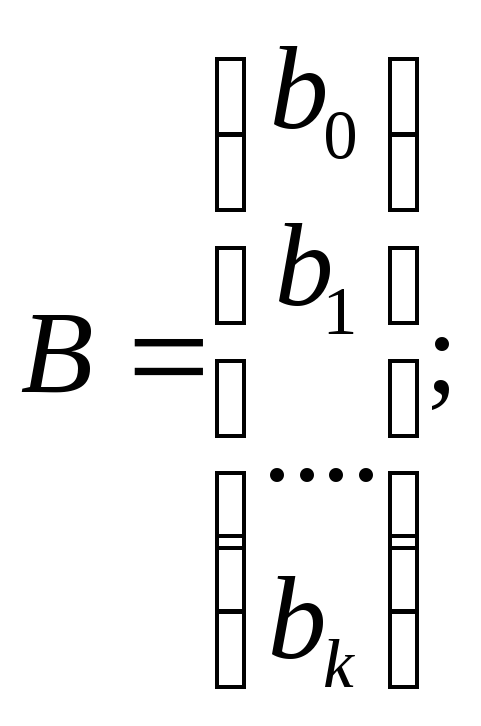
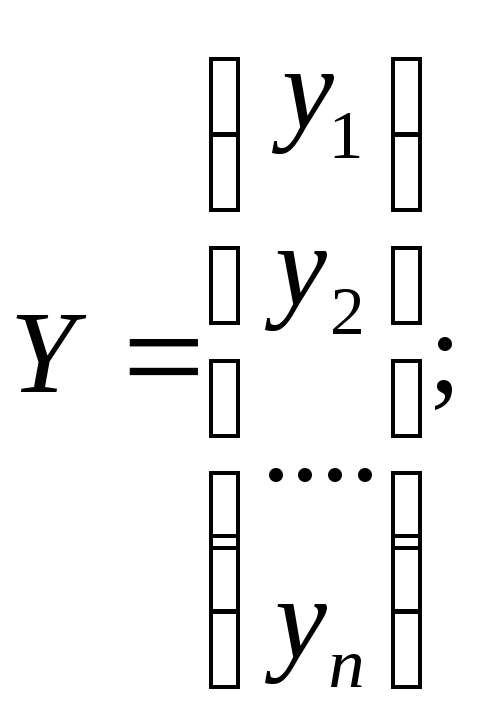
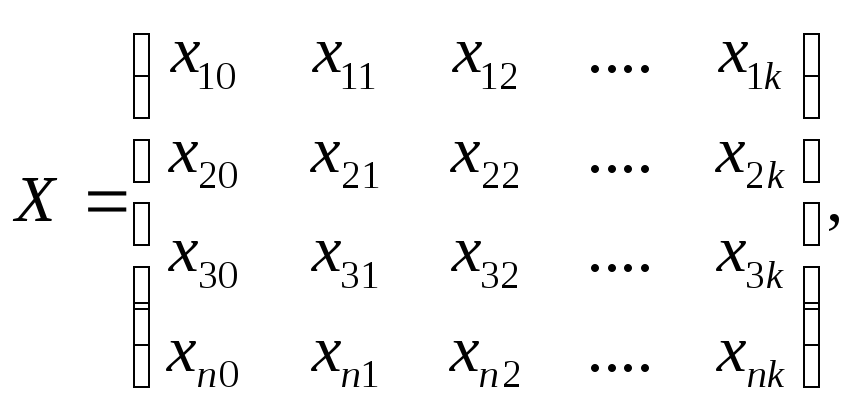
при х_j0 = 1, j =1,n;

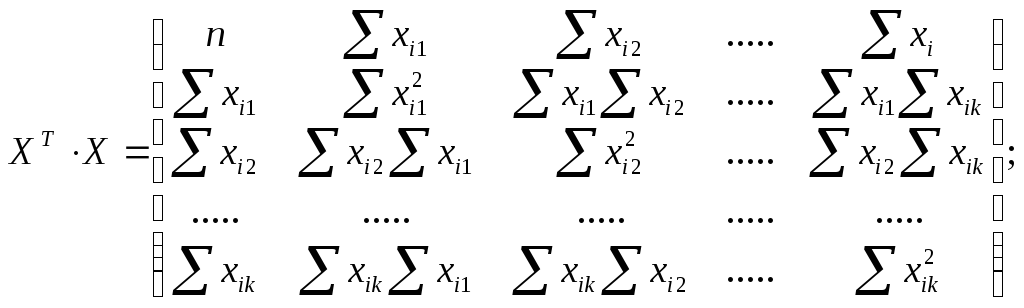
Умножая правую и левую части уравнения на обратную матри- цу (Х^T∙Х)^-1, при (Х^T∙Х)^-1∙(Х^T∙Х)^-1= Е = 1 получим:

(Х^T∙Х)^-1(Х^T∙Х)В= (Х^T∙Х)^-1(Х^T∙Y).

Откуда В=(Х^T∙Х)^-1(Х^T∙Y). Каждый коэффициент уравнения регрессии вычисляется по формуле

где с_ij — элементы обратной матрицы (Х^T∙Х)^-1.

Пример. В результате проведенных исследований влияния мощ- ности гумусового слоя почвы (Х₁) и количества внесенного слож- ного состава минерального удобрения (Х₂) на урожайность зерно- вой культуры (Y) получены уравнения:

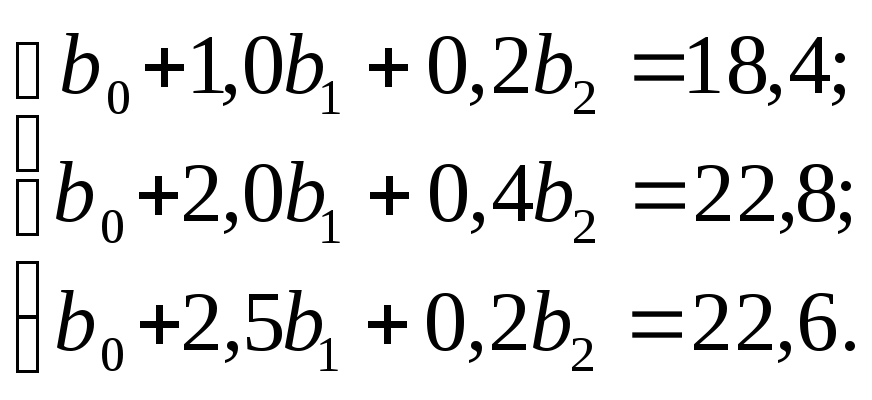
Установить форму связи урожайности е факторами х₁ и х₂ в виде линейного уравнения регрессии.

Р е ш е н и е. Представляем результаты опытов в виде матриц:

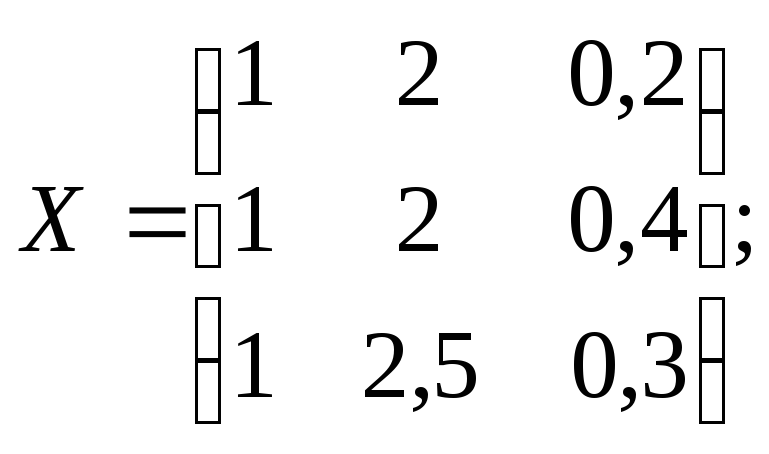
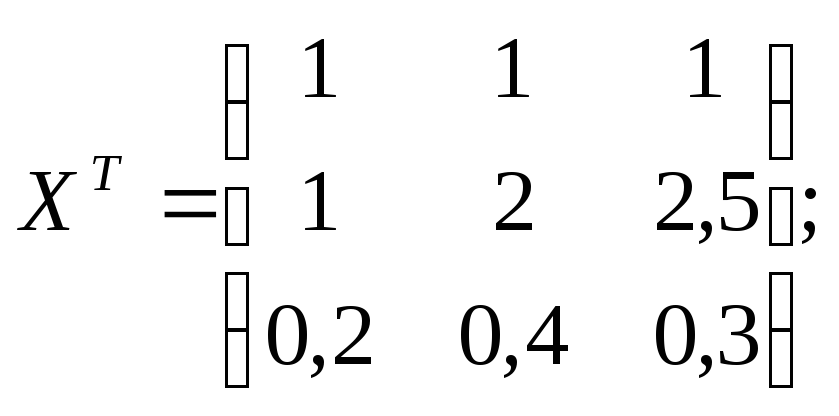
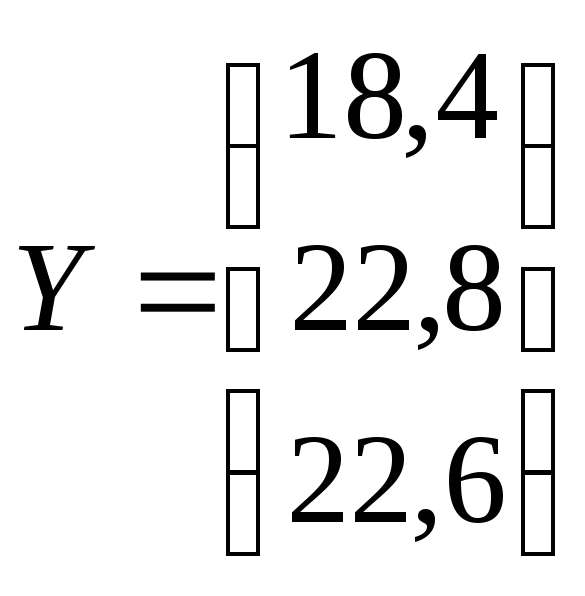
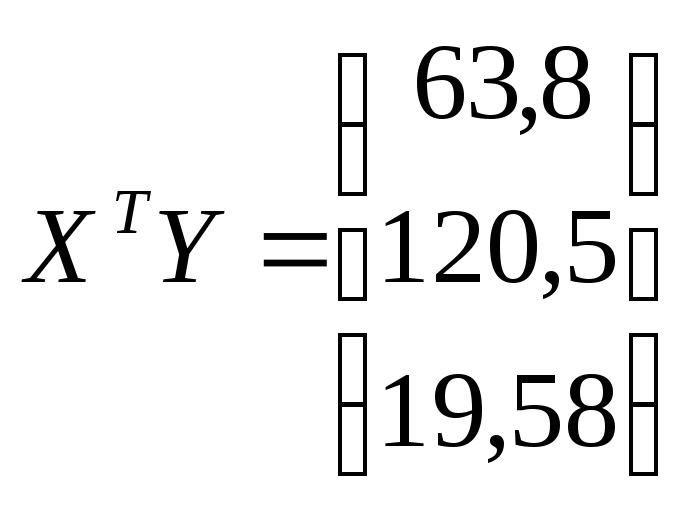
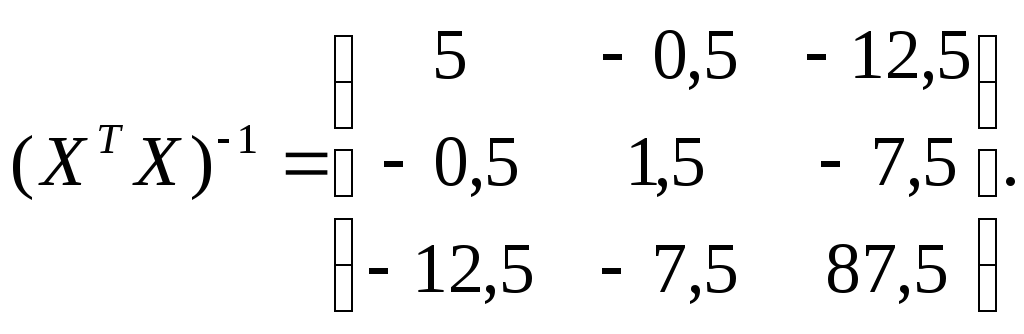
Определяем коэффициенты уравнения регрессии

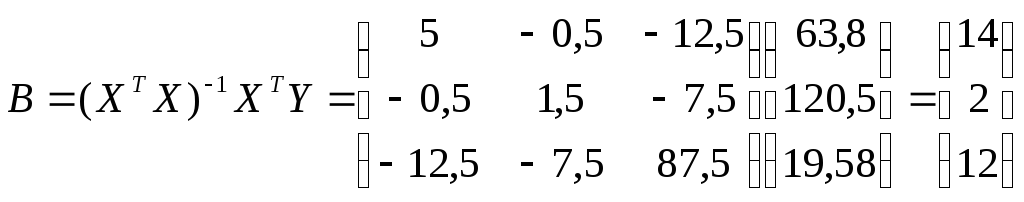
Отсюда b₀ = 14, b₁ = 2, b₂ = 12 и уравнение регрессии имеет вид

=14+2х₁ +12х₂.

Для проверки значимости уравнения регрессии необходимо при заданных значениях (х₁,х₂) провести несколько экспериментов, чтобы для данного значения (х₁,х₂) получить некоторое среднее значение функции у. В этом случае экспериментальный материал представляется, например, в виде табл. 7.1.

Таблица 7.1

Эксперименталъный материал исследования

№ п.п.	Уровни факторов		Значение функции y при паралельных опытах			Опытное среднее значение
	x1	x2	y1	y2	y3	yi
1	1,0	0,2	18,2	18,6	18,7	18,5
2	2,0	0,4	21,6	23,4	23,7	22,9
3	2,5	0,3	22,0	23,0	22,5	22,5

Число параллельных опытов, как правило, должно быть k > 3. Проверка значимости уравнения регрессии проводится по F-крите- рию. Для этого вычисляем остаточную дисперсию

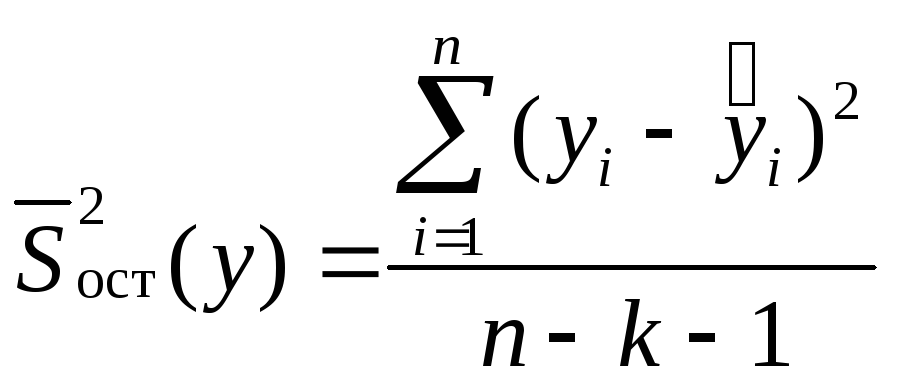
и затем вычисляем F_B — статистику

которую сравниваем с табличным значением при уровне значимости α и числе степеней свободы k₁ = n - 1; k₂ = n - k -1 (см. приложение 6, в, с). Гипотеза о значимости уравнения регрессии принимается при условии

F_B≥

Значимость коэффициентов регрессии проверяют по t-кри- терию. Статистику

сравнивают с при уровне значимости α и степени свободы k = n - k -1 (см. приложение 2).

Погрешность коэффициента регрессии определяется по фор- муле

где — диагональный элемент матрицы (Х^TХ)^-1. Доверительный интервал для коэффициентов регрессии определяем по формуле

где — значение коэффициента регрессии в генеральной совокупности.

Пример. По результатам опытов, приведённым в табл. 7.1 получено уравнение регрессии у =14+2х₁ +12х₂. Проверить значимость уравнения регрессии.

Р е ш е н и е. Данные представим в виде, удобном для вычислений (табл. 7.2).

Определяем остаточную дисперсию

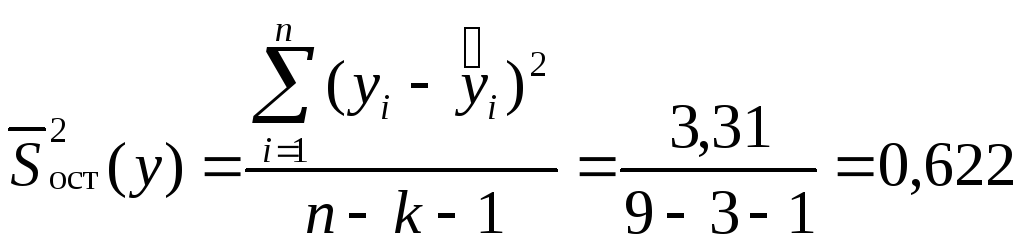
И дисперсию для у

Таблица 7.2