Вычисление данных для линеаризации уравнения регрессии

Х	Y	lny	xlny	x2
1	0,5	- 0.3010	- 0,3010	1
2	1,0	0	0	4
3	1,4	0,1461	0,4383	9
4	1,7	0,2304	0,9216	16
5	1,8	0,2553	1,2765	25
6	1,9	0,2788	1,6728	36
7	2.0	0,3010	2,1070	49
∑=28	10,3	0,9106	6,1152	140

После преобразований получим: а = 0,6; b = 1,226. Следовательно, уравнение регрессии для зависимости толщины слоя ила от толщины снежного покрова будет иметь вид:

=

В табл. 5.7 даны нормальные уравнения МНК для некоторых функций.

Таблица 5.7

Нормальные уравнения мнк для некоторых функций

Функции	Нормальные уравнения
y = a+bx	an + b∑x =∑у; a∑ + b∑х2 = ∑ху
у = аЬxсx2	nlga + lgb∑x + lgс∑х2 = ∑lgy lga∑x + lgb∑x2 + lgc∑x3 = ∑lgxlgy; lg∑x2+lg∑x3+lg∑4 =∑х2lgy
lgy = a+ bx	an + b∑ = ∑lgy; a∑х + b∑x2 = ∑xlgy
y = а+ bx+ сх2	na + b∑х + с∑х2 =∑у а∑х + b∑x2 + с∑х3 = ∑ху a∑x2+ b∑x3 + с∑x4 =∑x2у
у =аbx	nlga+ lgb∑x = ∑lgy lga∑x + lgb∑x2 = ∑lg xlg y
y = a+b - lgx	an+ b∑lgx = ∑у a∑lgх + b∑(lnх)2= ∑lgxlgy

Рассмотрим второй случай — метод наименьших квадратов для нелинейных форм. Пусть Y — целевая функция; у₁, у₂, ..., у_n — набор ее наблюдений; х₁, х₂, ..., х_n — переменные факторы. Наблюдения представляют из себя вектор

X_i = (x_1i, x_2i, ..., x_mi).

Необходимо целевую функцию Y выразить через вектор Х посредством функции f, вид которой известен, однако неизвестны некоторые её параметры d₁, d₂, ..., d_k. Тогда для Y_i можно записать

Y_i = f_i(d₁, d₂, ..., d_k; x₁, x₂, ..., x_mi) + F_i ,

где F_i — отклонение (ошибка).

Если исключить параметры d₁, d₂, ..., d_k то функция запишется в виде

Y_i = f_i(х„.,х„,,х„„.) + F_i,

куда входят параметры, которые необходимо найти МНК.

Минимизируя

и используя метод Маркварда, введем векторы

; ; ; ,

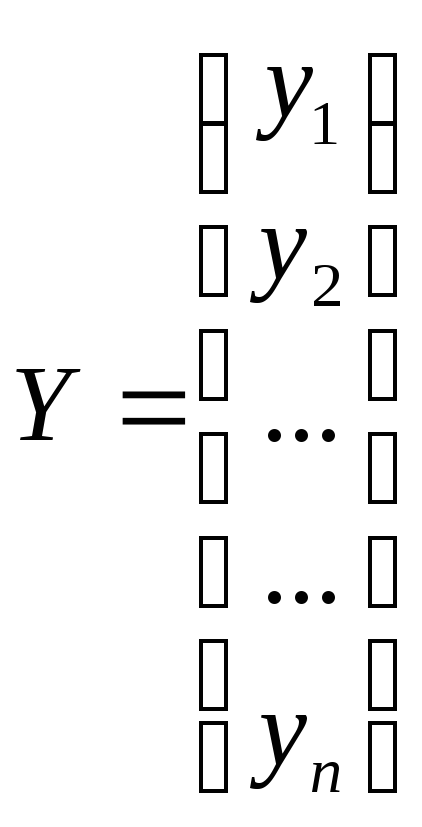сформируем задачу в виде: найти такое Х*, что при F = Y — f целевая функция (сумма квадратов остатков) S = F^TF минимизируется.

Приближенное значение Х_i, получаемое на t-том шаге итеративного процесса, и последующее приближенное значение Х_t+1 связаны между собой вектором поправки ∆Х, т.е.

Формула вектора поправки ∆Х согласно условию минимизации, выводится из решения системы линейных уравнений

откуда = -(А^TА)^-1 A^тF,

где А — первая частная производная от F, определяемая как матрица Якоби приx=x_t

Это формулы итерации по методу Ньютона — Гаусса. При их использовании, если степень нелинейности f(х) высока, а стартовое значение х далеко отстоит от минимизирующего значения, то велика вероятность «раскачки» и расходимости итеративного процесса.

Левенберг и Марквардт в процедуре Ньютона — Гаусса предложили искать корректирующий вектор ∆Х из уравнения

(A^тA +v²I) ∆Х = - А^тF;

где I — единичная матрица, а v— некоторая величина, называемая числом Марквардта. Тогда

∆Х = -( A^тА + v²I)^-1 А^тF.

При v = 0 приходим к формуле ∆Х= -( A^тА + v²I)^-1 А^тF. При вычислениях рекомендуется за начальное значение принимать v =0,001, затем на каждом шаге увеличивать v в десять раз, до тех пор, пока S не начнет уменьшаться.