Выборка из генеральной совокупности

xi	5	7	9	11	13	15	17	19	2,1
mi	15	26	25	30	26	21	24	20	13

Решение. По выборке определяем и S².

.

Составляем статистическую таблицу (табл. 2.11). Для столбца четыре вычисляем статистику

и_i = (x_i -)/S.

Например,

и_{i =} = -1,62 и т.д.

По статистике и_i находим р_i по таблицам для нормального распределения (см. приложение 9).

p_i = φ(u_i).

Например,

p_i = φ(u₁) = φ(-1,62) = 0,1074 и т.д.

Теоретическую частоту вычисляем с учетом ширины интервала результатов наблюдения n = х_i+1 - х_i = 2 по формуле

т_i,T = nhφ(и_i)/S.

Например, для х₁

m_i,T = = 9,15 и т.д.

Таблица 2.11

Статистическая таблица

Номер		Частота mi	Статистика ui	Вероятность pi	Теорети- ческая частота mi,т	Относительная разность частот
интервала	варианта xi
1	2	3	4	5	6	7
2	5	15	— 1,62	0,1074	9,15	3,74
3	7	26	— 1,20	0,1942	16,55	5,39
4	9	25	— 0,77	0,2966	25,27	0,01
5	11	30	— 0,35	0,3752	32,00	0,13
6	13	26	0,08	0,3977	33,90	0,23
7	15	21	0,51	0,3503	29,85	2,62
8	17	24	0,93	0,2589	22,05	0,17
9	19	20	1,36	0,1582	13,50	3,13
10	21	13	1,78	0,0818	7,0	5,14
		200	-	-	189,27	20,56

и заполняем столбец 7, в котором определяем относительную разность частот

например, = =3,74 и т.д.

Суммируя по всем интервалам, получим:

По таблице (см. приложение 3) находим

= 12,6

Так как

,

то гипотезу Н₀ о нормальном распределении генеральной совокуп- ности отвергаем, т.е. эмпирические и теоретические частоты разли- чаются значимо.

назад

Лекция 5.

Построение и анализ экологических моделей. Регрессионный анализ.

При построении математических зависимостей могут быть две формы связей между функцией и переменными: функциональная и регрессионная. Если функциональные связи точно выражаются аналитическими уравнениями, то регрессионные связи выражаются уравнениями лишь приближенно. В общем случае можно сказать, что связь между функцией и аргументами будет тогда функциональной, когда будут учтены все аргументы, определяющие значения функции.

Уравнение регрессии составляется исследователем на основе характера связи между функцией и аргументами. Вопрос о форме связи решается, как правило, поэтапно.

Вначале рассматривается линейная форма связи вида:

Y = b₀ + b₁X₁ +b₂X₂ +...+ b_n X_n

где Х_i — факторы (i = 1, 2, ..., n), так как такая форма связи часто встреча-

ется на практике и для нее разработан хороший математический математический аппарат.

При этом могут решаться следующие задачи:

• установление точности определения коэффициентов уравнения регрессии b_i в виде значений дисперсии S² (b_i) или величины доверительных интервалов;

• установление значимости коэффициента b_i;

• проверка адекватности установленной формы связи и экспериментальных данных.

При установлении тесноты связи между Y и Х решается задача установления строгости соблюдения функциональной зависимости между изменениями Y и Х. Для оценки тесноты связи между случайными переменными величинами используются показатели:

а) в случае линейной формы связи

• коэффициент парной корреляции r_yx или r_xy, характеризующий строгость соблюдения пропорциональности, т.е. близость ис- следуемой формы связи с линейной;

• коэффициент частной корреляции ,характеризующий тесноту связи между изучаемыми переменными при условии, что влияние остальных факторов исключается;

• коэффициент множественной корреляции ,характеризующий суммарное влияние всех факторов на величину Y;

б) в случае нелинейной формы связи

• корреляционное отношение р, которое является характеристи- кой, насколько строго соблюдается функциональная связь между исследуемыми переменными. Этот показатель применим и для оценки тесноты связи в случае линейной формы связи. В этом случае он равен абсолютному значению коэффициента парной корреляции;

• множественное корреляционное отношение ,которое является характеристикой тесноты связи между Y и Х. Аппарат корреляционно-регрессионного анализа используется в двух направлениях:

1) для проведения статистического анализа результатов наблюдений пассивных экспериментов, в которых независимые переменные Х. не могут изменяться экспериментатором, т.е. не регулируются. В результате такого анализа решение вопроса о виде формы связи не является окончательным, т.е. можно принять в качестве математической модели процесса большое число уравнений регрессии, которые могут удовлетворять полученным экспериментальным данным;

2) совместно с методом наименьших квадратов для планирования статистических экспериментов и анализа их результатов. В этом случае планирование экспериментов осуществляется в соответствии с принятым видом уравнения связи Y и Х.

В соответствии с числом учитываемых независимых переменных Х_i и характером связи между Y и Х различают:

а) по количеству исследуемых переменных

• парный корреляционно-регрессионный анализ;

• множественный корреляционно-регрессионный анализ;

б) в зависимости от формы связи

• линейный корреляционно-регрессионный анализ;

• нелинейный корреляционно-регрессионный анализ.

Метод наименьших квадратов. Широкое распространение в практике математического моделирования получили уравнения регрессии вида:

у =f(х),

где х — величина, которая рассматривается как случайная независимая переменная;

у — случайная зависимая величина. При линейной форме связи эту зависимость можно выразить уравнением прямой:

Y=b₀ + b₁Х,

для построения, которого требуется проведение экспериментов в объеме n, в каждом из которых должна фиксироваться пара значений (х_i; у_i). Результаты эксперимента представляются либо в виде таблицы (табл. 5.1), либо в виде графиков (рис. 5.1).

Таблица 5.1

Значение фактора Хi	Х1	Х2	...	Хi	...	Хn
Значение функции Yi	Y1	Y2	...	Yi	...	Yn

Представление результатов эксперимента

Рассматривая экспериментальные точки (х_i; у_i) в прямоугольной системе

Рис. 5.1. График результатов эксперимента

координат, мы видим, что в случае рис. 5.1. а) часть точек лежит на прямой Y = b₀ +b₁Х, часть ниже и выше ее. В этом случае для построения модели зависимости Y от Х можно использовать линейное уравнение регрессии. В случае рис. 5.1. б) — нелинейное уравнение, а в случае рис. 5.1. в) применение регрессионного анализа проблематично.

Рассмотрим случай а), здесь через совокупность точек проведена прямая

Y = b₀ +b₁Х которая показывает на существование зависимости между Х и Y и наша задача состоит в том, чтобы определить коэффициенты b₀ и b₁ определяющие положение прямой относительно всех и экспериментальных точек таким образом, чтобы сумма квадратов отклонений между значениями у_i, полученными при эксперименте и значениями у при х_i, подставленное в предлагаемое (гипотетическое) уравнение, было минимальным. Для этого используется метод наименьших квадратов (MHK).

Пусть разность между экспериментальным у_i и гипотетическим значениями у равна при х_i δ = у_i - у, или δ = у_i - (b₀ +b₁Х). При изменении величин b₀ и b₁ меняется, и δ. Возьмем функцию

являющуюся функцией двух переменных b₀ и b₁. Наилучшая пря- мая, описывающая зависимость Y от Х для экспериментальных данных будет такая, где значение

Для нахождения минимума возьмём частные производные от S(b₀,b₁) и приравняем их к нулю.

Решая эту систему, называемую системой нормальных уравнении МНК, получим:

Коэффициент b₀ — есть постоянная уравнения, которая определяется при

х = 0, а b₁ — угол наклона прямой регрессии Y к оси 0Х

В качестве меры зависимости между случайными величинами используется коэффициент корреляции, определяемый по формуле

Коэффициент корреляции всегда находится в пределах — 1< r <+1. Если случайные величины Х и Y независимы, то r = 0; если связь между Х и У функциональная, то r = 1. В качестве меры адекватности регрессионной модели статистическим данным часто используют коэффициент детерминации

Где — расчетное значение (теоретическое по полученному уравнению

регрессии = b_o + b₁х, где знак «ˆ» над у обозначает, что уравнение по- лучено по МНК для величины Y от Х_i,

где — среднее значение у

—значения у в i-том опыте (i =1, 2, ..., n).

Чем больше значения R², тем выше степень адекватности уравнения регрессии опытным данным.

Для уравнения регрессии вида

у =bo+b₁х₁ +b₂х₂+…+b_iх_i+…+b_mх_m;

многих переменных х,, х, ..., х„, результаты i го опыта записываются в виде

у =b_ox_0i+b₁х_1i +b₂х_2i +…+b_mх_mi;

где x_0i= 1 при всех i =1,n,.

n — общее число опытов в эксперименте.

Для определения коэффициентов уравнения регрессии b₀, b₁, b₂, ..., ,b_m, может быть использован МНК, который минимизирует сумму квадратов регрессионных опытов

Если представить результаты эксперимента в матричной форме Y = ХВ,

где ; ; .

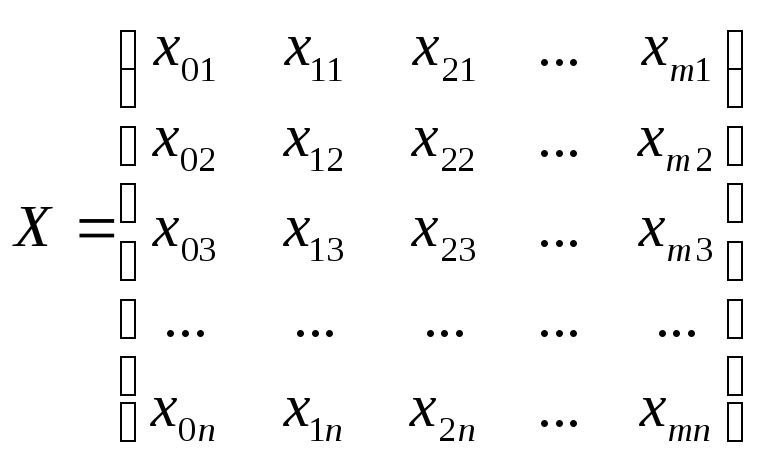то можно записать S = (Y — XB)^T(Y — XB) (индекс «т» означает транспонирование).

Исходя из условий минимизации , откуда (X^TX)B = X^TY.

Следовательно, оценка МНК есть такая, при которой коэффи- циенты уравнения регрессии равны В = (X^TX)^-1Х^TУ (индекс "-1" означает обратную матрицу). Коэффициент детерминации (скорректированный) равен:

Оценка меры автокорреляции случайной величины, как правило, производится с помощью статистики Дарбина-Уот- сона

При значении D(δ), близком к двум, говорят, что автокорреляция отсутствует (что желательно).

Пример. В результате эксперимента зафиксированы пары значений (х_i,у_i), приведенных в табл. 5.2: Построить уравнение регрессии вида у = b₀+b₁х

Таблица 5.2