4.4. Статистические оценки гипотез об экологических моделях

Построенные экологометрические модели требуют оценки их достоверности. При выполнении статистических исследований полученные данные тщательно анализируются на предмет удовлетворения их предположения о независимости случайных наблюдений, симметричности распределения, из которого получена выборка, равенства дисперсии ошибок, одинаковости распределения нескольких случайных величин и т.д. Все эти предположения могут рас- сматриваться как гипотезы, которые необходимо проверить. Понятие «статистическая гипотеза» — более узкое, чем общее понятие «научная гипотеза». Статистические гипотезы охватывают поведение наблюдаемых случайных величин.

Статистическая гипотеза, являющаяся утверждением о значениях параметров конкретного вероятного распределения некоторой случайной величины (например, о средней дисперсии) называется параметрической.

Статистическая гипотеза является:

а) утверждением о некоторых свойствах вероятности распределений исследуемых случайных величин, (например, симметричности распределения, совпадения функций распределения двух и более случайных величин, принадлежности выборки к данному классу вероятностного распределения);

б) независимым от вида вероятности распределения утверждением о параметрах случайных величин, например, равенстве двух или более средних арифметических или дисперсии (при неизвестных вероятностных распределениях этих случайных вели- чин), относится к параметрическим гипотезам. Проверка статистических гипотез осуществляется с помощью статистических критериев.

Выдвигаемая гипотеза, которую необходимо проверить, называется нулевой и обозначается H₀. Гипотеза, которая противопоставляется нулевой, называется альтернативной и обозначается Н₁. Выделение нулевой гипотезы состоит в том, что H₀, обычно рассматривается как утверждение, которое более важно, если оно отвергнуто. Это основано на общем принципе, согласно которому теория должна быть отвергнута, если есть противоречащий пример, но не обязательно должна быть принята, если такого примера найти нельзя.

Если конкурирующие гипотезы H₀ и H₁ полностью определяют распределение случайной величины х, например значение пара- метра Θ равным Θ(H₀) или Θ(H₁), соответственно такие гипотезы называются простыми.

Гипотезы называются сложными, если они не полностью определяют параметры распределения. Например, если согласно некото- рой гипотезе случайная величина распределена по нормальному за- кону со средней М(х) и неизвестной дисперсией D(x), то в этом случае будем иметь дело со сложной гипотезой. Гипотеза H₁ альтернативная H₀ тоже может быть сложной. Например, если по ги- потезе H₁ случайная величина распределена по нормальному закону с известной D(x) и средней М₁(х) > М₀(х) или М₁(х)≠М₀(х), то очевидно, что гипотеза H₁, не определяет полностью распределение, поэтому ее следует считать сложной.

Таким образом, если распределение имеет всего k параметров, часть которых неизвестна, то гипотеза также называется сложной.

Необходимо получить критерий, с помощью которого по наблюдаемому значению х можно сделать разумный выбор между нулевой и альтернативной гипотезами. Построение критерия начинается с выбора такого множества на действительной прямой (или в n-мерном пространстве), что если случайная величина примет значение из этого множества, то принимается нулевая гипотеза (H₁ отвергается). Такое множество называют множеством принятия гипотезы (W₀). Дополнительное множество к множеству W₀ называется множеством отклонения гипотезы H₀(W₀), или критическим множеством.

При проверке гипотезы H₀ против H₁ возможны два рода ошибок. Ошибки первого рода — это ошибка, когда принимается неверная гипотеза H₀. Вероятность ошибки первого рода принято обозначать α, она называется уровнем значимости критерия. Обычно α выбирают равным: 0,10; 0,05; 0,025 и 0,01.

Вероятность ошибки второго рода обозначают β. Вероятность дополнительного события, т.е. правильного отклонения гипотезы H₀ называется мощностью критерия. Следовательно, мощность критерия (W_кр) равна вероятности того, что наблюдение попадает в критическую область, если оно имеет альтернативное распределение, т.е. W_кр = 1 - β.

Процедура применения статистического критерия следующая.

1. Выдвигаются гипотезы H₀ и H₁ и задается уровень значимости α. На выбор уровня значимости может влиять отношение исследователя к гипотезе до проведения эксперимента. Если есть уверенность в истинности гипотезы, то необходимы убедительные свидетельства, чтобы отказаться от этой уверенности. В таких условиях нужны критерии высокого уровня и α выбирается очень малой, чтобы попадание в критическую область было крайне неправдоподобным, если верна гипотеза H₀.

2. Выбирается статистический критерий проверки H₀ при уровне значимости α с критерием связана статистика критерия Г=Г(х₁, х₂, ..., х_n), которая является выборочной функцией с известн- ным вероятностным распределением F(γ). Критическая область W находится как подмножество выборочного пространства х, такое, что вероятность

Р(Г W| H₀) ≥ α.

В зависимости от альтернативной гипотезы

а)H₁: Θ_b < Θ;

б)H₁: Θ_b > Θ;

в) H₁: Θ_b ≠ Θ,

критическая область выражается через значения статистики Г и принимает одну из форм:

а) Г≤ Г₀;

б) Г≥Г_и;

в) Г≤Г_а или Г≥Г_в,

где Г₀, Г_и, Г_а, Г_в - квантили известного распределения, выбранные так, что при выполнении H₀ справедливо одно из соотношений:

а) Р_r(Г ≤ Г₀) = α;

б) Р_r(Г≥ Г_и) = α;

в) Р_r(Г ≤Г_а) или Р_r(Г ≥ Г_в) = α /2.

Случаи а) и б) представляют односторонние критические области, а случай в) - двустороннюю критическую область; Р_r - вероятность принятия гипотезы.

С критической областью W для данного критерия при уровне значимости α однозначно связан доверительный интервал, которому соответствует вероятность

Р(Г W| Н₀) ≥1 — α..

3. Если вычисленная по выборке статистика Г имеет значение

Г = Г(х₁, х₂ , ..., х_n),

которое не принадлежит W то гипотеза Н₀ принимается, в противном случае она отвергается и принимается гипотеза Н₁. Возможен и другой подход. Пусть Г - вычисленное значение статистики по выборке. Вычислим вероятность Р_a попадания Г в критическую область. Эта вероятность называется фактически достигнутым уровнем значимости. Значение Р дает возможность при- нимать или отвергать гипотезу при любом заранее заданном уровне значимости а путем простого сравнения Р_a с α. Если Р_a меньше α, то гипотеза Н₀ отвергается с уровнем значимости α, в противном случае Н₀ принимается.

Лекция 4. (продолжение).

Проверка статистических гипотез о равенстве средних. При ис- следовании часто возникает вопрос о сравнении центров распределения двух или более случайных величин. Здесь важно выяснить, являются ли полученные статистические оценки математического ожидания по разным выборкам оценкой одного и того же математического ожидания для определенного закона распределения F(х).

При проверке гипотез о равенстве средних вначале необходимо проверить гипотезу о независимости одинаково нормально распре- деленных случайных величин в выборке (х₁, х_2, ..., х_n) при неизвес- тных параметрах М(х) и D(x). Выборку записывают в том же порядке, в каком записывались результаты наблюдений, например, (42, 63, 23, 47, 52, 98, 97, 73, 85, 88). По имеющейся выборке вычисляем D(x) двумя способами:

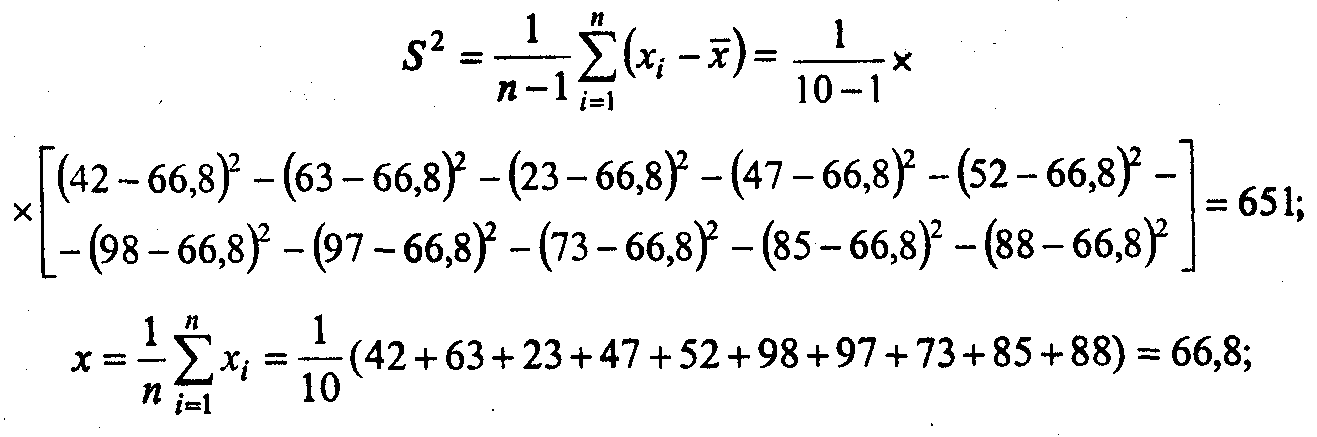
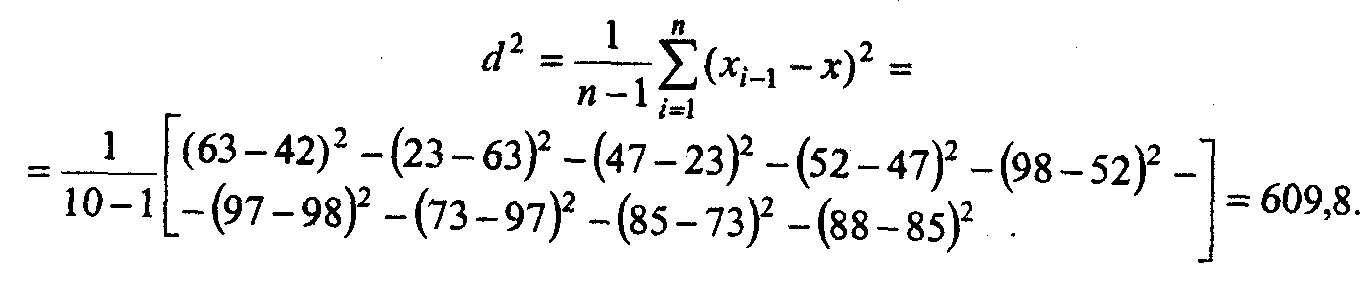
Определяют статистику q = d²/2S²

Гипотеза о независимости случайных величин Н₀ принимается если

q ≥ q_n(α),

где q(α) — табличное значение статистики q при объеме выборки n и уровне значимости α (см. табл. 2.7) принимаем α = 0,010 тогда q₁₀ = 0 3759.

При уровне значимости α = 0,01 гипотеза о независимости Н₀ принимается, это говорит о том, что наблюдения имеют систематический сдвиг математических ожиданий.

Если принять, α=0,05, то q₁₀(0,05) = 0,5311, тогда Q=0,468< q₁₀ (0,05) = 0,5311.

В этом случае гипотеза Н₀ отвергается и принимается гипотеза о зависимости результатов наблюдений Н₁ т.е. наблюдения не соде- ржат систематического сдвига математических ожиданий. При n>60 для вычисления q_n(α) используется формула

где n — объем выборки;

и_α - критерий, определяемый при заданном α, как F(u_α)=1-α, и определяется по таблице (см. приложение 1).

Гипотеза Н₀ о независимости случайных величин принимается при условии

q ≥ q_n²(α).

Проверка гипотез о равенстве средних в зависимости от условий проводится по разным критериям. Рассмотрим их.

Таблица 2. 7

Значения q-статистики

n	α	qn(α)
5	0,001 0,010 - 0,050	0,2080 0,2690 0,4102
10	0,001 0,010 0,050	0,2408 0,3759 0,5311
20	0,001 0,010 0,050	0,3926 0,5203 0,6498
30	0,001 0,010 0,050	0,4822 0,5975 0,7091
40	0,001 0,010 0,050	0,5425 0,6467 0,7461
50	0,001 0,010 0,050	0,5853 0,6814 0,7718
60	0,001 0,010 0,050	- - 0,7906

1. Проверка гипотезы о равенстве средних двух выборок, сделанных из нормально распределенной совокупности с известной величиной дисперсии D(х) и D(y), при n_x>30 и n_y>30 осуществляется сравнением статистики z_b равной

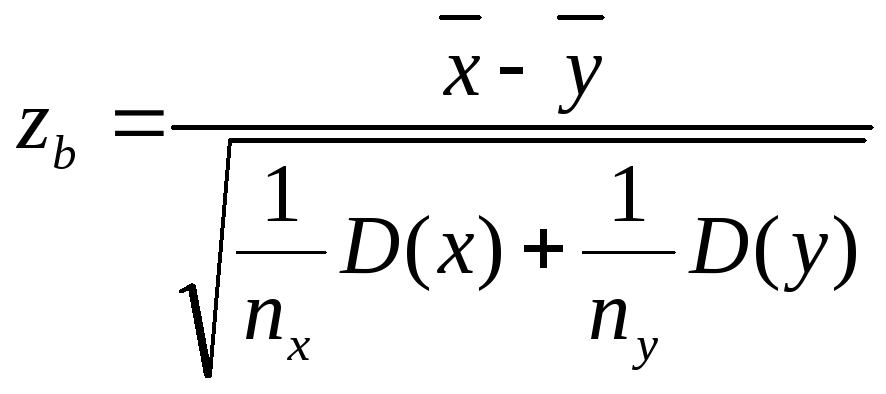
и критического значения z_α, определяемого как

где а — уровень значимости;

z_α — значение, определяемое по таблицам (см. приложение 1) при и= z_α.

Гипотеза Н₀ о равенстве средних принимается, если |z_b|<z_α. В противном случае, когда |z_b| > z_α гипотеза Н₀ отвергается и прини- мается гипотеза Н₁ о том, что средние нельзя считать равными т.е. выборки n_x и n_y сделаны из разных генеральных совокупностей.

Пример. При испытании двух типов фильтров для очистки воздуха в объемах n_x= n_y = 50 штук получено среднее значение чистоты воздуха х = 92%, у = 96%. Проверить, является ли рас- хождение значений х и у случайными, если известны D(x)= 0,09%; D(y) = 0,04%.

Решение. Выдвигаем гипотезу Н₀: М(х) = М(у). Определяем статистику

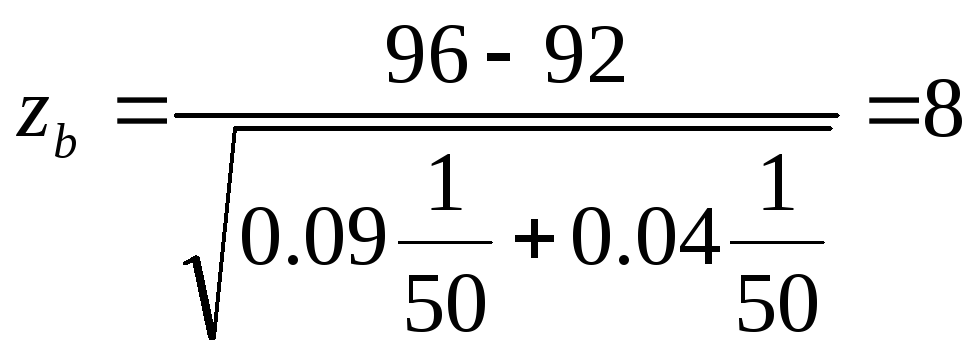
При уровне значимости, а = 0,05, находим:

По таблице (см. приложение 1) находим и =z_a и z_a = 1,96.

Сравниваем z_b = 8 >z_a = 1,96. Следовательно, гипотеза Н₀ отвергается, так как имеются качественные различия между двумя типами фильтров.

2. При малых объемах выборок: n_x < 30, n_y < 30, по которым найдены и и выборочные дисперсии S_x² и S_y² гипотезу Н₀: М(х) =М(у) проверяют вычислением статистики при альтерна- тивной гипотезе Н₁: М(х) w М(у).

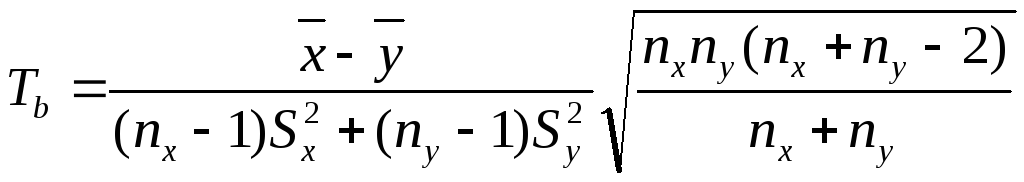
Гипотеза Н₀ принимается при условии |Т_b| < t_a,k, где t_a,k — табличное значение критерия Стьюдента при заданном уровне значи- мости а и числе степеней свободы K= n_x+n_y-2 (см. приложение 2). При |Т_b| <t_a,k гипотеза Н₀ отклоняется и принимается альтернативная гипотеза Н₁: М(х) w М(у).

Пример. При исследовании местности случайным образом были отобраны 16 участков (n_x=16) и установлено среднее число пораженных болезнью растений = 350 с дисперсией =16. Проверить, является ли расхождение среднего числа пораженных растений случайным или же болезнь пошла на убыль.

Решение. Выдвигаем гипотезу Н;. М(х) = М(у) при уровне значимости а = 0,05 и определяем статистику Т_b

По таблицам (см. приложение 2) находим

T_0.05;16+20-2=t_0.05;34 = 2.03.

Сравниваем Т =1,188 < 1_0.05;34=2,03.

Следовательно, принимаем гипотезу Н₀: М(x) = M(у), т.е. различие в среднем числе пораженных растений, измеренном в различные моменты времени, в данном случае объясняется случайностью выборок.

3. Если выборка объемом n сделана из генеральной совокупно- сти нормально распределенных величин х с известными М(х) = а_k, D(x) = а², то при уровне значимости а можно проверить гипотезу Н₀: a = a₀ — предполагаемое значение математического ож идания. Предложение о величине а_о делается либо по результатам выборки n, либо по имеющейся априорной информации о генеральной совокупности.

Для проверки гипотезы Н₀: а=а₀ вычисляется статистика и_b при конкурирующей гипотезе Н₁: a ≠ а_о

Критическое значение и_α определяется по таблице (см. приложение 1) по заданному значению , как

Гипотеза Н₀ принимается при условии

альтернативная гипотеза Н₁: а ≠ а₀ принимается при условии

Пример. Разработанная схема очистки промышленных стоков дает экономический эффект 88 руб. с 1т при среднем квадратическом отклонении

=5 руб./т. Обследовано сто очистных сооружений (n =100) и определен средний экономический эффект = 90 руб./т. Требуется при уровне значимости = 0,05 проверить гипотезу Н₀: а ≠ а₀.

Р е ш е н и е. Определяем статистику и_b

По таблице (см. приложение 1) находим и_a

откуда u_0,05 = 1,96. Сравниваем u_b = 4 >u_0,05 = 1,96.

Следовательно, гипотеза Н₀: а = а₀ отклоняется, т.е. выбороч- ное и гипотетическое среднее различаются значимо.

4. При неизвестной дисперсии D(x) проверка гипотезы Н₀: а ≠ а₀, при конкурирующей гипотезе Н₁: а ≠ а₀ проводится с помощью статистики

где и S² — соответственно выборочные средние и дисперсия.

Критические значения статистики t_a,k при заданном уровне значимости а и числе степеней свободы k = n - 1 выбирается по таблице (см. приложение 2).

Если Т_b< t_a,k, то тогда принимается гипотеза Н₀, при Т_b >t_a,k гипотеза Н₀ отклоняется и принимается гипотеза Н₁.

5. Имеется k выборок (k >2) из нормальных генеральных совокупностей с равными, но неизвестными дисперсиями. Необходимо проверить гипотезу о равенстве средних Н₀: а₁ =а₂ = ... =а_k при заданном уровне значимости α. Альтернативная гипотеза Н₁ гово- рит о том, что средние различны.

Для проверки гипотезы Н₀ вычисляем статистику

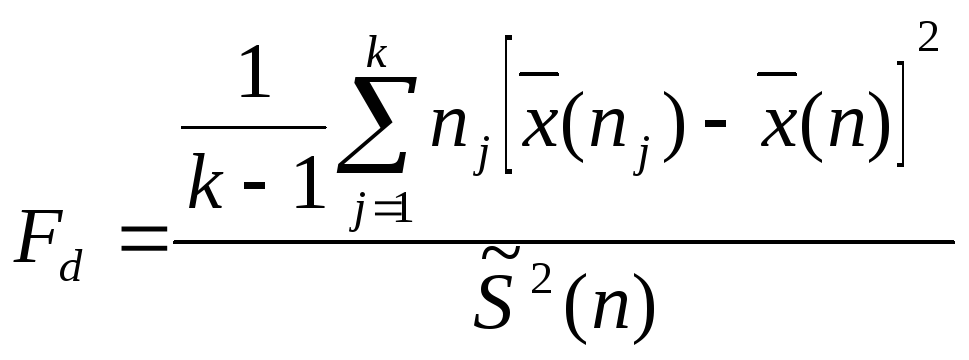
где

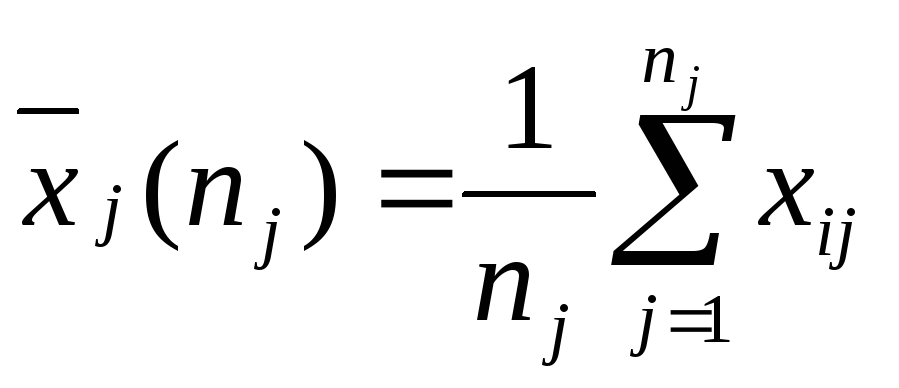
Гипотеза Н₀принимается при

и отвергается при

где — табличное значение критерия при уровне значимости α и степенях свободы р₁ = k — 1; р₂ = n — k которое выбирается по таблице (см. приложение 6).

Пример. Имеется три выборки (k = 3), n₁ = 3, n₂ =4, n₄=5 (n =12).

Вычисленное значение F_b = 0,43.

Решение. При α =0,05: р₁= 3 - 1= 2; р₂ = 12 - 3 = 9;

F_1-0,05;2,9 = 4,26. Тогда F_b = 0,43 < F_1-0,05;2,9 = 4,26, т.е. гипотеза о равенстве средних должна быть принята.

Проверка статистических гипотез о равенстве дисперсии. Дисперсии играют в экологии очень важную роль, поскольку измеряемая дисперсией величина рассеивания характеризует такие важные показатели, как колебание точности тех или иных технологических процессов, например, зараженности различных участков местности, загрязненности участков водоемов и т.д. Средняя величина как бы сглаживает эти колебания, а дисперсия их выявляет.

Для проверки гипотез о равенстве дисперсий в различных генеральных совокупностях по независимым выборкам необходимо знать такую функцию статистических оценок, распределение которой не зависело бы от каких-либо неизвестных параметров.

Предположим, что независимые случайные величины х₁, х₂, ..., х_n1, распределены по закону F(x) с параметрами М(х) и D(x), которые известны. Имеются также независимые нормально распределенные F(y) случайные величины у₁, у₂, ..., у_n1 параметры M(y) и D(y) кото- рых также известны. Нужно проверить гипотезу Н₀: о равенстве D(x)=D(y), предполагая, что эти два множества Х и У независимы. При малых и средних объемах выборок для проверки гипотезы Н₀: D(x) = D(y) используется статистика

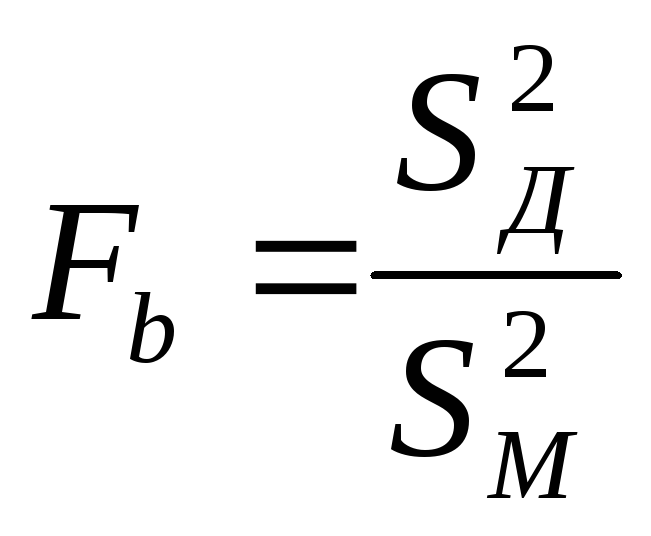
где и — дисперсии, определяемые по выборкам n_x и n_y, причем в

числитель ставится большая из двух дисперсий и .

Выборочное значение F_b сравнивается с критерием Фишера при заданном уровне значимости α и числах степеней свободы k₁ = n_x - 1; k₂ = n_y - 1. Справедливость гипотезы Н₀ подтверждается при условии

F_b ≤

значение определяется по таблице (см. приложение 6).

При F_b > гипотеза Н₀ отвергается и принимается аль- тернативная гипотеза Н₁: D(x) ≠ D(y).

Пример. Для проверки точности дозировки двух автоматов при упаковке химического вещества отобраны от первого автомата 21 проба (n_x = 21), от второго — 15 (n_y = 15). По отобранным пробам , определены выборочные среднеквадратические отклонения в дозировке S_x = 20г, S_y = 15г. Проверить гипотезу о том, что автоматы имеют одинаковую точность, т.е. Н₀: D(x) = D(y), при уровне зна- чимости α = 0,10 и конкурирующей гипотезе Н₁: D(x) ≠ D(y).

Решение. Вычисляем выборочную статистику

=

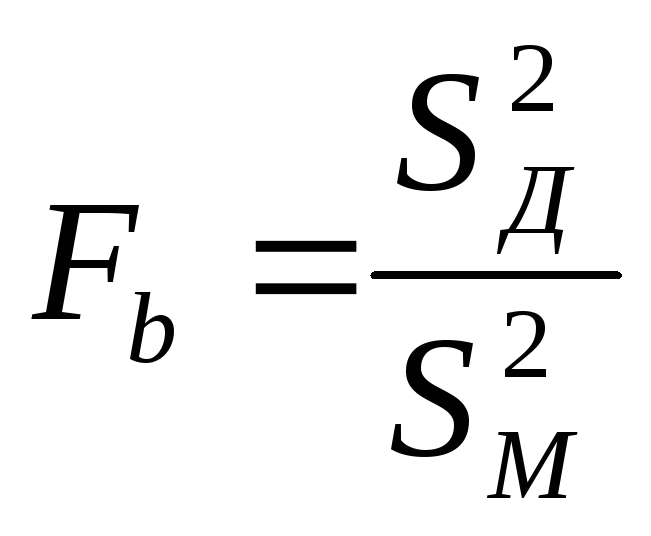По уровню значимости, а = 0,10 и числу степеней свободы k₃ = n_x — 1;

k_M= n_y — 1, т.е. k₃ = 14; k_M= 20 находим по таблице F_1-a/2;14,20 = 2,23 (см. приложение 6). Сравниваем

F_b = 3,06 > F_1-a/2;14,20 = 2,23.

Следовательно, гипотезу Н₀ о равной точности автоматов отвергаем, так как разницу в дозировке химического вещества нельзя объяснить случайностью.

При больших объемах выборки статистику F_b можно определять по формуле:

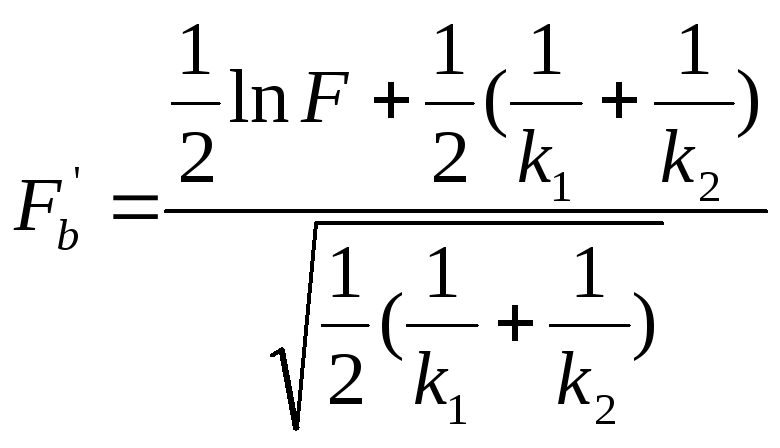
где .

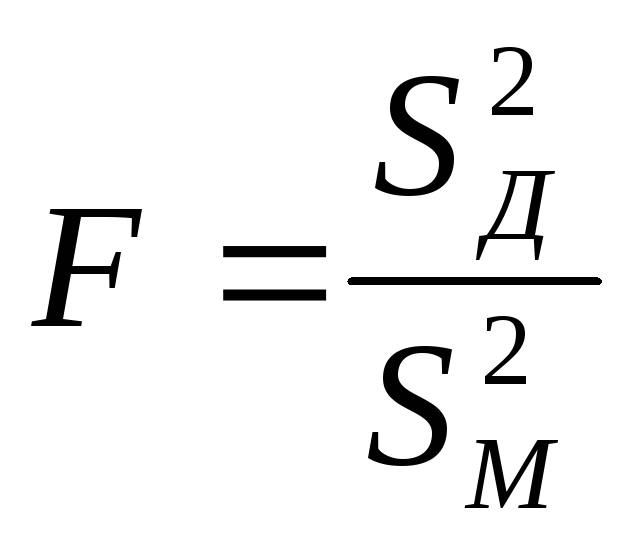При проверке гипотезы Н_о: D(x) = D(y) сравнивают F'_b и U_1-a/2, где — уровень значимости; U_1-a/2 — квантиль уровня (1 — а/2) стандартного нормального распределения (см. приложение 1). При F'_b < U_1-a/2,

где Ф(U_1-a/2) = 1 — а/2 и х = U_1-a/2, гипотеза Н₀ принимается, в противном случае, когда F'_b ≤ U_1-a/2, Н₀ отвергается и принимается гипотеза Н₁: D(x) ≠ D(y).

Если взята одна выборка n из генеральной совокупности, для которой предполагаемое значение дисперсии равно , хотя сама дисперсия D(x) неизвестна, то можно проверить при заданном уров- не значимости гипотезу Н₀: D(x) = , при альтернативной гипоте- зе Н₁: D(x) ≠ . Для проверки гипотезы Н_о определяют статистику

где S² — выборочная дисперсия;

—гипотетическая дисперсия.

Гипотеза Н₀ принимается, если удовлетворяется условие

;

в противном случае принимается альтернативная гипотеза Н₁, где k — число степеней свободы, k = n — 1.

Критерий Пирсона и принимается по таблице (см. приложение 3).

Пример. Для проверки правильности высева семян взяты 20 участков. Отклонение от нормы высева оценивалось среднеквадратическим отклонением числа семян на участке, оно составило S =16 семян. Требуется при заданном уровне значимости а = 0,1 прове- рить нулевую гипотезу Н_о: D(x) =, при норме = 225. Конку- рирующая гипотеза Н₁: D(x) ≠.

Р е ш е н и е. Определяем — статистику

При = 0,10 и k = 20 — 1 =19 определяем по таблице (см. приложение 3)

Записываем условие

,

т.е. принимается гипотеза Н₁: D(x) = . Это означает, что сеялка настроена правильно в соответствии с заданной нормой и точностью высева.

Если исследуется нормально распределенные совокупности х₁, х₂, ..., х_p, из которых извлечены независимые выборки n₁, n₂, ..., n_p различных объемов, для которых определены дисперсии , , ..., ,то при заданном уровне значимости можно проверить гипотезу Н₀: D(x₁) = D(x₂) = ... = D(х_p) по критерию Бартлетта. Для этого определяют статистику

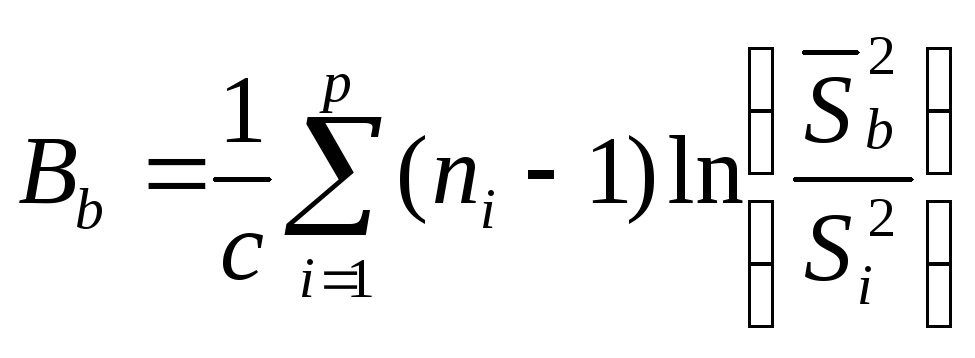
где

Величина является оценкой генеральной дисперсии D(x). Гипотеза Н₀ принимается при условии

;

где k — число степеней свободы, k = р - 1; величина принимается по таблице (см. приложение 3). Критерий Бартлетта очень чувствителен к отклонениям от нормального распределения выборочных совокупностей. Если выборки равны n₁, n₂, ..., n_p, то для проверки гипотезы Н₀: D(x₁) = D(x₂) = ... = D(x_p) используют критерий Кохрена (Кочрена). Для проверки гипотезы Н₀ вычисляют статистику

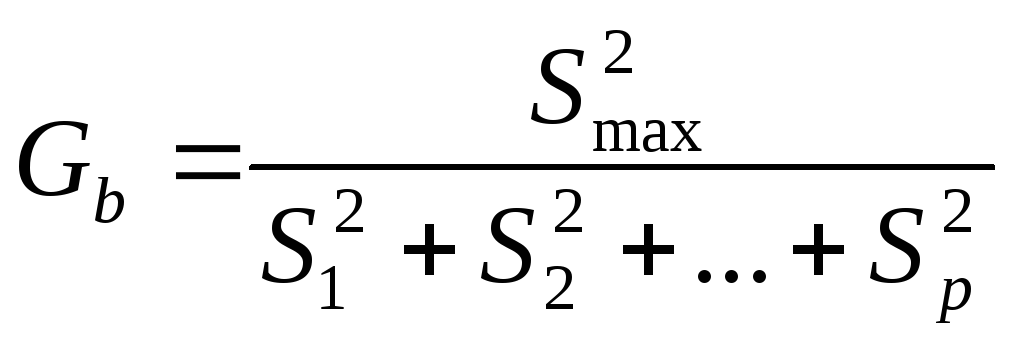
где — максимальная дисперсия из р дисперсий, т.е.

Полученное значение G_b сравнивают с критическим значением , k = n - 1; n — объем одной выборки. Гипотеза Н₀ принимается при условии

в противном случае принимается гипотеза Н₁: D(x₁) ≠ D(x₂) ≠ ... ≠ D(x_p). Значение принимается по таблице (см. приложение 7). Пример. На 17 предприятиях региона в течение семи месяцев изучалась загрязненность промышленных стоков. Вычисленные эмпирические дисперсии для каждого из этих месяцев оказались равными: 0,067; 0,136; 0,168; 0,068; 0,066; 0,102; 0,107. Необходимо проверить гипотезу Н₀ об отсутствии существенного различия в загрязненности промышленных стоков за семь месяцев. Решение. Вычисляем статистику

При уровне значимости = 0,05; р =7; k =17 — 1 =16; F_1-0,05;7;16= 0,27 (см. приложение 7). Тогда

G_b = 0,235 < F_1-0,05;7;16 = 0,27,

т.е. гипотеза H₀ об отсутствии существенного различия в загрязненности промышленных стоков в течение семи месяцев принимается. Проверка статистических гипотез об однородности выборок. Для проверки однородности независимых выборок (х₁, х₂,..., х_p) и (у₁, у₂, ..., у_n2) случайных величин х и у выдвигаем нулевую гипотезу H₀ о равенстве функций распределения H₀: F(x) = F(y), при уровне значимости и конкурирующей гипотезе Н₁: F(x) ≠ F(y). Если объем каждой из выборок не превосходит 25, проверку гипотезы H₀ проводят с помощью статистики W_b. Для определения W_b статистики располагают варианты обеих выборок в возрастающем порядке (табл. 2.8). Например, для выборок n_x: 3, 4, 6, 10, 13, 17 и n_y: 1, 2, 5, 7, 16, 20, 22 общий ряд будет иметь вид

Таблица 2.8