2.3. Элементы ядерной физики Справочные сведения

Символическая запись атомного ядра

,

где - символ химического элемента,- зарядовое число, совпадающее с атомным номером (число протонов в ядре),- массовое число (сумма числа протонов и нейтронов в ядре).

Разность суммы масс покоя входящих в ядро нуклонов и массы покоя ядра называется дефектом массы

,

где - масса протона,- масса нейтрона,- масса ядра.

Энергия связи ядра вычисляется по формуле

,

где при практических расчетах удобно использовать массу, выраженную в атомных единицах массы, а квадрат скорости света .

Для расчетов энергии связи (дефекта масс) удобнее пользоваться выражением, куда входят не массы ядер, а массы нейтральных атомов:

,

где - масса атома водорода,- масса атома данного химического элемента.

Удельная энергия связи (энергия связи на нуклон)

.

Энергия, выделяющаяся (поглощающаяся) в ходе ядерной реакции, вычисляется по формуле

,

где в первой скобке стоит сумма масс покоя частиц, вступающих в реакцию, а во второй – сумма масс покоя продуктов ядерной реакции.

Символическая запись ядерной реакции может быть дана в развернутом виде, например,

,

или в сокращенном виде

.

В ходе любой ядерной реакции должны выполняться законы сохранения зарядового и массового чисел.

Символические обозначения некоторых частиц, участвующих в ядерных реакциях: - протон,- нейтрон,- дейтрон (ядро изотопа водорода),- тритон (ядро изотопа водорода),- альфа-частица (ядро изотопа гелия),- электрон,- позитрон,- нейтрино,- антинейтрино,- гамма-квант.

Закон радиоактивного распада

,

где - число радиоактивных атомов в начальный момент времени,- число нераспавшихся атомов к моменту времени,- постоянная радиоактивного распада.

Период полураспада (промежуток времени, в течение которого распадается половина первоначального количества радиоактивных атомов) связан с постоянной распада соотношением

.

Величина, обратная постоянной распада

,

называется средним временем жизни радиоактивного атома.

Активность радиоактивного образца определяется как отношение числа ядер, распавшихся в изотопе, к промежутку времени, за которое произошел распад

.

Примеры решения задач

Задача 1. Определить энергию, которая может выделиться при образовании из протонов и нейтронов одного моля гелия .

Решение

Вычислим дефект массы процесса, в ходе которого из двух протонов и двух нейтронов образуется ядро атома гелия. Поскольку в таблицах приведены массы покоя атомов, а не ядер, добавим к каждому протону по электрону (в результате получится атом водорода), а к ядру атома гелия добавим два электрона (в результате получится атом гелия). В результате получим

. (2.3.1)

Используя табличные данные (,,), находим

(2.3.2)

При помощи (2.3.2) определяем энергетический эффект от слияния протонов и нейтронов в атом гелия

.

Как известно, число частиц в одном моле любого вещества равно постоянной Авогадро, поэтому при образовании из протонов и нейтронов одного моля гелия должна выделиться энергия

.

Задача 2. Под действием протонов могут происходить реакции термоядерного деления:

а) ; б).

Какие изотопы используются в качестве мишеней в этих реакциях? Определить энергию , выделяющуюся в ходе реакций.

Решение

Для ответа на первый вопрос воспользуемся законами сохранения зарядового и массового чисел. Для первой реакции это позволяет записать уравнения

, ,

решая которые получаем

, ,

что позволяет при помощи таблицы Менделеева определить первую мишень:

.

Аналогичные вычисления для второй реакции дают ответ:

.

Теперь аналогично задаче 1 определяем энергетический выход реакция, предполагая, что кинетической энергией бомбардирующих мишени протонов можно пренебречь:

а) ;

б) .

Сравнение полученных значений с энергией покоя протона , показывает, что использованное при решении пренебрежение кинетической энергией протона справедливо только для нерелятивистских протонов.

Задача 3. Протоны с кинетической энергией бомбардируют литиевую мишень, в результате чего наблюдается ядерная реакция. Найти кинетическую энергию каждой альфа-частицы и угол между направлениями их разлета, если разлет происходит симметрично по отношению к направлению налетающих протонов.

Решение

Воспользуемся для решения задачи законами сохранения импульса и энергии. Суммарная кинетическая энергия альфа-частиц очевидно равняется сумме кинетической энергии протона и энергетическому выходу ядерной реакции:

. (2.3.3)

Обозначая угол, который образует импульс альфа-частицы с импульсом протона через , и проектируя закон сохранения импульса на направление движения протона, получаем

. (2.3.4)

Используя классическую формулу связи кинетической энергии и импульса (это оправдано, так как рассматриваемые в задаче энергии намного меньше энергий покоя участвующих в реакции частиц)

(2.3.5)

и формулу энергетического выхода ядерной реакции

, (2.3.6)

из (2.3.3), (2.3.4) находим

, (2.3.7)

. (2.3.8)

Подстановка в (2.3.7), (2.3.8) числовых значений с учетом найденного при решении предыдущей задачи энергетического выхода реакции дает:

,

.

Задача 4. За время начальное количество некоторого радиоактивного изотопа уменьшилось враза. Во сколько разоно уменьшится за время?

Решение

Воспользуемся законом радиоактивного распада

. (2.3.9)

Согласно условию задачи

, . (2.3.10)

Логарифмируя первое из уравнений (2.3.10), получаем

,

что после подстановки во второе уравнение (2.3.10) дает

.

Задача 5. Известно, что из радиоактивного полония массойза времядня в результате его распада образуется гелий объемомпри нормальных условиях. Определить по этим данным период полураспада данного изотопа полония.

Решение

Начальное число атомов полония найдем из формулы молекулярно-кинетической теории

. (2.3.11)

Число распавшихся атомов полония в предположении, что не происходит других реакций альфа-распада, будет равно образовавшемуся числу атомов гелия, которое можно определить при помощи уравнения состояния идеального газа

. (2.3.12)

Из закона радиоактивного распада находим

, (2.3.13)

что после подстановки (2.3.11), (2.3.12) дает уравнение

. (2.3.14)

Учитывая формулу связи постоянной распада и периода полураспада 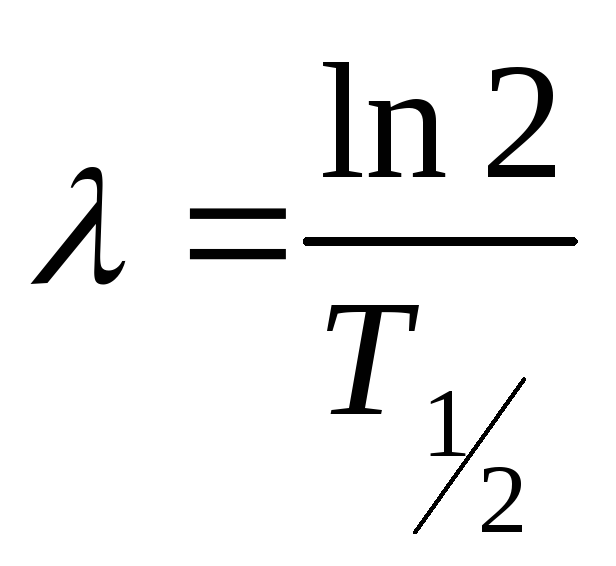и решая уравнение (2.3.14) с учетом, находим значение периода полураспада

.