где - номера орбит,- радиусй орбиты, а- скорость электрона на ней,- постоянная Планка.

Радиусы электронных орбит в атоме водорода (водородоподобном ионе)

,

где - заряд ядра,- радиус первой орбиты (для атома водорода (- первый боровский радиус).

Энергия электрона в стационарном состоянии атома водорода (водородоподобного иона)

,

где - энергия основного состояния (для атома водорода).

Согласно гипотезе де Бройля любой частице, обладающей импульсом, сопоставляется волновой процесс с длиной волны

.

Фазовая и групповая скорость волн де Бройля

, .

Соотношение неопределенностей Гейзенберга для координат и импульсов

, ,.

Соотношение неопределенностей для энергии и времени

.

Вероятность нахождения частицы в элементе объема вычисляется по формуле

,

где - волновая функция частицы.

Вероятность найти частицу в момент времени в конечном объемеопределяется по формуле

.

Условие нормировки волновой функции имеет вид

.

Среднее расстояние электрона от ядра вычисляется по формуле

.

Уравнение Шредингера для волновой функции имеет вид

,

где - оператор Лапласа,- потенциальная функция частицы в силовом поле,- мнимая единица.

Стационарное уравнение Шредингера записывается в виде

,

где - полная энергия частицы.

Собственные функции частицы, находящейся в одномерной прямоугольной бесконечно глубокой потенциальной яме имеют вид

,

где - ширина ямы. Собственные значения энергии для этой задачи записываются в виде

.

Примеры решения задач

Задача 1. Вычислить индукцию магнитного поля в центре атома водорода, обусловленного движением электрона по первой боровской орбите.

Решение

Запишем уравнение движения электрона в атоме (второй закон Ньютона)

(2.2.1)

и правило квантования электронных орбит с учетом того, что движение происходит по первой орбите ()

. (2.2.2)

Решая систему (2.2.1), (2.2.2), найдем радиус орбиты и скорость электрона на ней

, (2.2.3)

. (2.2.4)

При помощи формул (2.2.3), (2.2.4) находим период обращения электрона

.

Сила эквивалентного тока, вызванного вращением электрона равна

. (2.2.5)

Используя теперь формулу индукции в центре кольца с током, при помощи (2.2.3), (2.2.5) находим

.

Подстановка числовых значений приводит к ответу

.

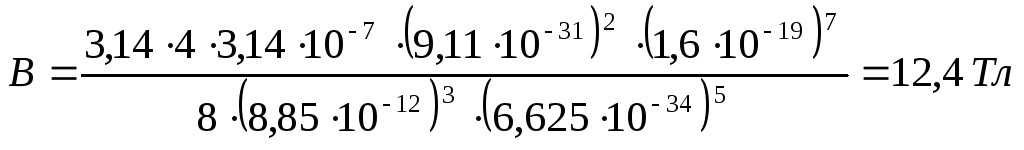Задача 2. Найти квантовое число , соответствующее возбужденному состоянию иона, если при переходе в основное состояние этот ион испустил последовательно два фотона с длинами волни.

Решение

Воспользуемся вторым постулатом Бора, согласно которому энергия излученного (поглощенного) кванта света равна разности энергий стационарных состояний атома

. (2.2.6)

Перейдем в этом выражении от частоты к длине волны по формуле и используем выражение для энергии стационарного состояния водородоподобного иона

. (2.2.7)

В результате получим

, (2.2.8)

где - постоянная Ридберга. Согласно условию задачи атом переходит в основное состояние в два этапа, излучая последовательно два фотона. Пусть квантовое число, соответствующее промежуточному состоянию атома, равно. Тогда, применяя два раза уравнение (2.2.8), получаем

, (2.2.9)

. (2.2.10)

Складывая уравнения (2.2.9), (2.2.10), находим

,

откуда следует

.

Задача 3. Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки, если длина волны коротковолновой границы сплошного рентгеновского спектра .

Решение

Предположим, что столкновение электрона с антикатодом является абсолютно неупругим, и в результате электрон полностью теряет свою кинетическую энергию, передавая ее фотону рентгеновского излучения. Тогда по закону сохранения энергии

, (2.2.11)

где с учетом релятивистского характера движения электрона для его кинетической энергии необходимо использовать формулу

. (2.2.12)

Решая систему (2.2.11), (2.2.12) относительно скорости электрона, после алгебраических преобразований находим

. (2.2.13)

С учетом релятивистской формулы для импульса выражение длины волны де Бройля примет вид

, (2.2.14)

и после подстановки (2.2.13) в (2.2.14) получаем

.

Подстановка в (2.2.14) числовых значений дает

.

Задача 4. Узкий пучок моноэнергетических электронов падает под углом скольжения на естественную грань монокристалла алюминия. Расстояние между соседними кристаллическими плоскостями, параллельными этой грани монокристалла. При некотором ускоряющем напряжениинаблюдали максимум зеркального отражения. Найти, если известно, что следующий максимум зеркального отражения возникал при увеличении ускоряющего напряжения враза. Считать выполненным условие.

Решение

Воспользуемся формулой Вульфа – Брэггов, определяющей условия дифракционных максимумов при дифракции на кристалле

. (2.2.15)

Применяя формулу (2.2.15) для двух случаев падения электронного пучка, получаем

, , (2.2.16)

где и- дебройлевские длины волн электронов,- номер максимума зеркального отражения.

Запишем выражение для длины волны де Бройля, используя классическую формулу связи импульса и кинетической энергии частицы

, (2.2.17)

где согласно теореме о кинетической энергии

(2.2.18)

(предполагаем, что начальной кинетической энергией электронов можно пренебречь).

Используя (2.2.17), (2.2.18), дебройлевские длины волн электронов можно записать в виде

, . (2.2.19)

Решая систему уравнений (2.2.16), (2.2.19), находим величину ускоряющего напряжения

.

Подстановка данных задачи дает

.

Задача 5. Оценить с помощью соотношения неопределенностей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.

Решение

Полагая неопределенности координаты и импульса равными координате и импульсу ,, из соотношения неопределенностей находим

. (2.2.20)

Полная энергия электрона в атоме складывается из его кинетической энергии и потенциальной энергии в кулоновском поле ядра

. (2.2.21)

С учетом (2.2.20) формулу для полной энергии можно записать в виде

. (2.2.22)

Так как по условию энергия электрона должна быть минимальной, исследуем на экстремум:

. (2.2.23)

Легко убедиться при помощи достаточного условия экстремума, что найденное значение обеспечивает минимум полной энергии электрона

. (2.2.24)

Расчеты по формулам (2.2.23), (2.2.24)

,

,

показывают, что в результате получился первый боровский радиус и энергия основного состояния атома водорода.

Задача 6. Найти решение нестационарного уравнения Шредингера для свободной частицы массы , движущейся в положительном направлении осис импульсом.

Решение

В случае свободного одномерного движения частицы () нестационарное уравнение Шредингера записывается в виде

. (2.2.25)

Будем решать данное уравнение методом разделения переменных, полагая, что искомая функция является произведением двух функций, одна из которых зависит только от пространственной координаты, а другая – только от времени:

. (2.2.26)

Подставляя (2.2.26) в (2.2.25) и разделяя переменные, получаем

. (2.2.27)

Так как левая часть (2.2.27) зависит только от времени, а правая – только от пространственной координаты, уравнение (2.2.27) может выполняться только в том случае, когда обе части этого уравнения равны одной и той же константе. Обозначим эту константу и запишем два получившихся уравнения

, . (2.2.28)

Сравнение второго уравнения (2.2.28) со стационарным уравнением Шредингера позволяет сделать вывод, что константа не что иное, как энергия частицы. С учетом этого общие решения уравнений (2.2.28) можно представить в виде

, .

Подставляя полученные решения в (2.2.26), находим

. (2.2.29)

Используя известные соотношения ,,, (2.2.29) можно переписать в виде

, (2.2.30)

из которого следует, что первое слагаемое представляет собой волну, движущуюся в положительном направлении оси , а второе – волну, движущуюся в отрицательном направлении этой оси. Согласно условиюи можно записать окончательный ответ

.

Задача 7. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна . Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчета координатыв середине ямы.

Решение

Согласно условию задачи потенциальная функция имеет вид

при ипри. Волновая функция должна обращаться в нуль на границах ямы

, , (2.2.31)

и удовлетворять одномерному стационарному уравнению Шредингера внутри ямы

. (2.2.32)

Введем обозначение ; тогда решение уравнения (2.2.32) записывается в виде

. (2.2.33)

Подстановка (2.2.33) в условия (2.2.31) дает систему линейных однородных уравнений

, . (2.2.34)

Система (2.2.34) имеет нетривиальное решение только в том случае, когда ее определитель равен нулю, что приводит к уравнению

,

решение которого записывается в виде

. (2.2.35)

В случае, когда - нечетное, из системы (2.2.34) получаем, если же- четное, то аналогично находим. Таким образом, решение задачи имеет вид

, ;,

Условие нормировки волновой функции позволяет определить амплитуду волновой функции:

(аналогично вычисляется ). Тогда нормированная волновая функция записывается в виде

;

Задача 8. Частица массы находится в одномерном потенциальном полев стационарном состоянии, гдеи- постоянные (). Найти энергиючастицы и вид функции, если.

Решение

Воспользуемся уравнением Шреденгера для стационарных состояний

(2.2.36)

и подставим в него выражение для волновой функции и ее второй производной . После сокращения на экспоненту получим уравнение

. (2.2.37)

Используя условие , из (2.2.37) находим

. (2.2.38)

Подставляя (2.2.38) в (2.2.37), находим вид потенциальной функции

.

Задача 9. Волновая функция, описывающая некоторую частицу, имеет вид , где- расстояние этой частицы до силового центра;- некоторая постоянная. Определить среднее расстояниечастицы до силового центра.

Решение

Предварительно найдем значение нормировочного коэффициента в выражении волновой функции, для чего используем условие нормировки вероятностей

. (2.2.39)

Учитывая, что элемент объема определяется по формуле , получаем

.

Полагая и, и интегрируя по частям, получаем

. (2.2.40)

Первое слагаемое в (2.2.40) равно нулю, а интеграл во втором слагаемом можно вычислить при помощи известного соотношения

,

с помощью которого получаем

,

что позволяет из (2.2.40) получить уравнение

. (2.2.41)

Решая (2.2.41), находим

. (2.2.42)

Для определения среднего расстояния от частицы до силового центра воспользуемся формулой

. (2.2.43)

Подставляя в (2.2.43) выражение для волновой функции с учетом (2.2.42) и интегрируя по частям, получаем

.