
- •Индивидуальные задания
- •Явления переноса. Справочные сведения
- •Примеры решения задач
- •Индивидуальные задания
- •2.3. Основы термодинамики Справочные сведения
- •Примеры решения задач
- •Индивидуальные задания
- •Поверхностное натяжение. Капиллярные явления. Справочные сведения
- •Примеры решения задач
- •Индивидуальные задания
Поверхностное натяжение. Капиллярные явления. Справочные сведения
Избыточная потенциальная энергия
молекул поверхностного слоя жидкости
![]() ,
где
,
где![]() - поверхностное натяжение,
- поверхностное натяжение,![]() - площадь слоя.
- площадь слоя.
Сила поверхностного натяжения
![]() .
.
Избыточное давление под искривленной
поверхностью жидкости (формула Лапласа)
![]() ,
где
,
где![]() и
и![]() - радиусы кривизны двух нормальных
сечений поверхности. Для сферической
поверхности
- радиусы кривизны двух нормальных
сечений поверхности. Для сферической
поверхности![]() .
.
Высота подъема жидкости в капилляре
![]() ,
где
,
где![]() - радиус капилляра,
- радиус капилляра,![]() - краевой угол ( при полном смачивании
- краевой угол ( при полном смачивании![]() ,
при полном несмачивании
,
при полном несмачивании![]() ).
).
Примеры решения задач
Задача 1. В двух капиллярных трубках
разного диаметра, опущенных в воду,
установилась разность уровней![]() .
При опускании этих же трубок в спирт
разность уровней оказалась
.
При опускании этих же трубок в спирт
разность уровней оказалась![]() .
Зная коэффициент поверхностного
натяжения воды
.
Зная коэффициент поверхностного
натяжения воды![]() ,
найти коэффициент поверхностного
натяжения спирта
,
найти коэффициент поверхностного
натяжения спирта![]() .
.
Решение
Высота подъема жидкости в капилляре определяется по формуле
![]() ,
,
где
![]() - коэффициент поверхностного натяжения,
- коэффициент поверхностного натяжения,![]() - радиус капилляра,
- радиус капилляра,![]() - краевой угол,
- краевой угол,![]() - плотность жидкости. Полагая смачивание
полным (
- плотность жидкости. Полагая смачивание
полным (![]() ),
находим для двух капилляров в случае
воды
),
находим для двух капилляров в случае
воды
![]() ,
,![]() ,
,
следовательно, разность уровней
![]() .
(2.4.1)
.
(2.4.1)
Аналогичные расчеты в случае спирта дают
![]() .
(2.4.2)
.
(2.4.2)
Из (2.4.1), (2.4.2) находим
![]() .
.
Отсюда коэффициент поверхностного натяжения ртути
 .
.
Задача 2. Капля ртути массой![]() введена между параллельными стеклянными
пластинами. Какую силу следует приложить,
чтобы расплющить каплю до толщины
введена между параллельными стеклянными
пластинами. Какую силу следует приложить,
чтобы расплющить каплю до толщины![]() .
Считать, что ртуть не смачивает стекло.
.
Считать, что ртуть не смачивает стекло.
Решение
Если жидкость не смачивает твердое тело, то давление под поверхностью жидкости оказывается больше внешнего давления на величину, определяемую по формуле Лапласа
![]() ,
(2.4.3)
,
(2.4.3)
где
![]() и
и![]() - радиусы кривизны двух взаимно
перпендикулярных сечений поверхности
жидкости.
- радиусы кривизны двух взаимно
перпендикулярных сечений поверхности
жидкости.
Сечение капли плоскостью, перпендикулярной
пластинам и проходящей через центр
капли представляет собой фигуру, две
стороны которой прямолинейны и
параллельны, а две другие – окружности
радиусом
![]() .
Сечение капли плоскостью, параллельной
пластинам дает окружность радиусом
.
Сечение капли плоскостью, параллельной
пластинам дает окружность радиусом![]() ,
найти который можно, вычисляя приближенно
(пренебрегая криволинейностью свободной
поверхности) объем капли.
,
найти который можно, вычисляя приближенно
(пренебрегая криволинейностью свободной
поверхности) объем капли.
Получаем
![]() ,
,
откуда следует
![]() .
(2.4.4)
.
(2.4.4)
Из (2.4.3), (2.4.4) находим
![]() .
.
Следовательно, сила давления на пластины равна
![]() .
.
Подставляя значения, получаем

Индивидуальные задания
2.4.1. При определении силы поверхностного
натяжения капельным методом число
капель глицерина, вытекающего из
капилляра, составляет
![]() .
Общая масса глицерина
.
Общая масса глицерина![]() ,
а диаметр шейки капли в момент отрыва
,
а диаметр шейки капли в момент отрыва![]() .
Определить поверхностное натяжение
глицерина. Ответ:
.
Определить поверхностное натяжение
глицерина. Ответ:![]() .
.
2.4.2. Какую силу
![]() необходимо приложить к горизонтальному
алюминиевому кольцу высотой
необходимо приложить к горизонтальному
алюминиевому кольцу высотой![]() ,
внутренним диаметром
,
внутренним диаметром![]() и внешним диаметром
и внешним диаметром![]() ,
чтобы оторвать его от поверхности воды?
Какую часть найденной силы составляет
сила поверхностного натяжения? Ответ:
,
чтобы оторвать его от поверхности воды?
Какую часть найденной силы составляет
сила поверхностного натяжения? Ответ:![]() ,
,![]() .
.
2.4.3. Кольцо внутренним диаметром
![]() и
внешним диаметром
и
внешним диаметром![]() подвешено на пружине и соприкасается
с поверхностью жидкости. Жесткость
пружины
подвешено на пружине и соприкасается
с поверхностью жидкости. Жесткость
пружины![]() .
При опускании поверхности жидкости
кольцо оторвалось от нее при растяжении
пружины на
.
При опускании поверхности жидкости
кольцо оторвалось от нее при растяжении
пружины на![]() .
Найти поверхностное натяжение жидкости.
Ответ:
.
Найти поверхностное натяжение жидкости.
Ответ:![]() .
.
2.4.4. Спирт по каплям вытекает из сосуда
через вертикальную трубку внутренним
диаметром
![]() .
Капли отрываются через время
.
Капли отрываются через время![]() одна после другой. Через какое время
вытечет масса
одна после другой. Через какое время
вытечет масса![]() спирта? Диаметр шейки капли в момент
отрыва считать равным внутреннему
диаметру трубки. Ответ:
спирта? Диаметр шейки капли в момент
отрыва считать равным внутреннему
диаметру трубки. Ответ:![]() .
.
2.4.5. Считая процесс образования мыльного
пузыря изотермическим, определите
работу, которую надо совершить, чтобы
увеличить его диаметр от
![]() до
до![]() .
Поверхностное натяжение мыльного
раствора принять равным
.
Поверхностное натяжение мыльного
раствора принять равным![]() .
Ответ:
.
Ответ:![]() .
.
2.4.6. Две капли воды радиусом
![]() каждая слились в одну большую каплю.
Считая процесс изотермическим, определите
уменьшение поверхностной энергии при
этом слиянии, если поверхностное
натяжение воды
каждая слились в одну большую каплю.
Считая процесс изотермическим, определите
уменьшение поверхностной энергии при
этом слиянии, если поверхностное
натяжение воды![]() .
Ответ:
.
Ответ:![]() .
.
2.4.7. Давление воздуха внутри мыльного
пузыря на
![]() больше атмосферного. Определите диаметр
пузыря. Поверхностное натяжение мыльного
раствора
больше атмосферного. Определите диаметр
пузыря. Поверхностное натяжение мыльного
раствора![]() .
Ответ:
.
Ответ:![]() .
.
2.4.8. Воздушный пузырек диаметром
![]() находится на глубине
находится на глубине![]() под поверхностью воды. Определите
давление воздуха в этом пузырьке.
Атмосферное давление примите нормальным.
Поверхностное натяжение воды
под поверхностью воды. Определите
давление воздуха в этом пузырьке.
Атмосферное давление примите нормальным.
Поверхностное натяжение воды![]() ,
а ее плотность
,
а ее плотность![]() .
Ответ:
.
Ответ:![]() .
.
2.4.9. Во сколько раз плотность воздуха в
пузырьке, находящемся на глубине
![]() под водой, больше плотности воздуха при
нормальном атмосферном давлении? Радиус
пузырька
под водой, больше плотности воздуха при
нормальном атмосферном давлении? Радиус
пузырька![]() .
Ответ: в
.
Ответ: в![]() раза.
раза.
2.4.10. В сосуд с ртутью опущен открытый
капилляр, внутренний диаметр которого
![]() .
Разность уровней ртути в сосуде и в
капилляре
.
Разность уровней ртути в сосуде и в
капилляре![]() .
Найти радиус кривизны мениска в капилляре.
Ответ:
.
Найти радиус кривизны мениска в капилляре.
Ответ:![]() .
.
2.4.11. Найти разность уровней ртути в двух
сообщающихся капиллярах, внутренние
диаметры которых равны
![]() и
и![]() .
Несмачивание считать полным. Ответ:
.
Несмачивание считать полным. Ответ:![]() .
.
2.4.12. Капилляр с внутренним радиусом
![]() опущен в жидкость. Найти поверхностное
натяжение жидкости, если известно, что
в капилляр поднялась масса жидкости
опущен в жидкость. Найти поверхностное
натяжение жидкости, если известно, что
в капилляр поднялась масса жидкости![]() .
Ответ:
.
Ответ:![]() .
.
2.4.13. Вертикальный капилляр длиной
![]() с запаянным верхним концом привели в
соприкосновение с поверхностью жидкости,
после чего она поднялась на высоту
с запаянным верхним концом привели в
соприкосновение с поверхностью жидкости,
после чего она поднялась на высоту![]() .
Плотность жидкости
.
Плотность жидкости![]() ,
диаметр внутреннего канала капилляра
,
диаметр внутреннего канала капилляра![]() ,
атмосферное давление
,
атмосферное давление![]() .
Найти коэффициент поверхностного
натяжения жидкости, считая смачивание
полным. Ответ:
.
Найти коэффициент поверхностного
натяжения жидкости, считая смачивание
полным. Ответ:![]() .
.
2.4.14. Какую силу
![]() надо приложить, чтобы оторвать друг от
друга (без сдвига) две смоченные
фотопластинки размером
надо приложить, чтобы оторвать друг от
друга (без сдвига) две смоченные
фотопластинки размером![]() ?
Толщина водяной прослойки между
пластинками
?
Толщина водяной прослойки между
пластинками![]() .
Смачивание считать полным. Ответ:
.
Смачивание считать полным. Ответ:![]() .
.
2.4.15. Между двумя горизонтальными
плоскопараллельными стеклянными
пластинками помещена масса
![]() ртути. Когда на верхнюю пластинку
положили груз массой
ртути. Когда на верхнюю пластинку
положили груз массой![]() ,
расстояние между пластинками стало
равным
,
расстояние между пластинками стало
равным![]() .
Пренебрегая массой пластинки по сравнению
с массой груза, найти поверхностное
натяжение ртути. Несмачивание считать
полным. Ответ:
.
Пренебрегая массой пластинки по сравнению
с массой груза, найти поверхностное
натяжение ртути. Несмачивание считать
полным. Ответ: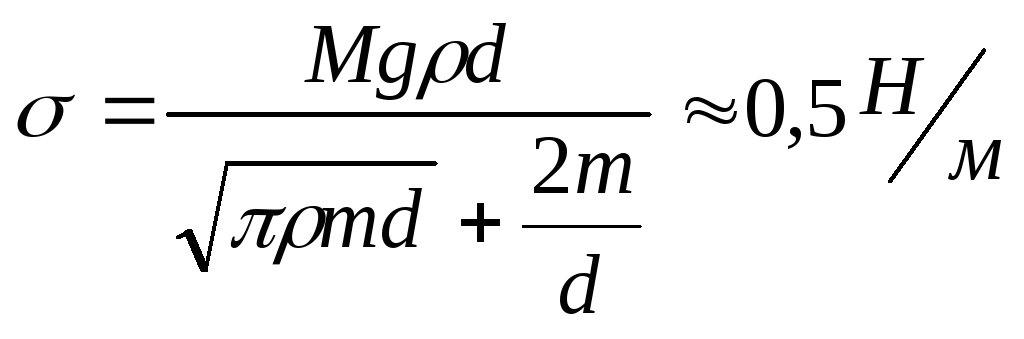 .
.
