
Формулы_математический_анализ
.docПределы
1![]() .
Бесконечно малые
функции:
.
Бесконечно малые
функции:
![]()
Бесконечно большие функции:
Если
![]() ,
то
,
то
![]() ;
;
Если
![]() ,
то
,
то![]()
2 .
Первый
замечательный предел:
.
Первый
замечательный предел:
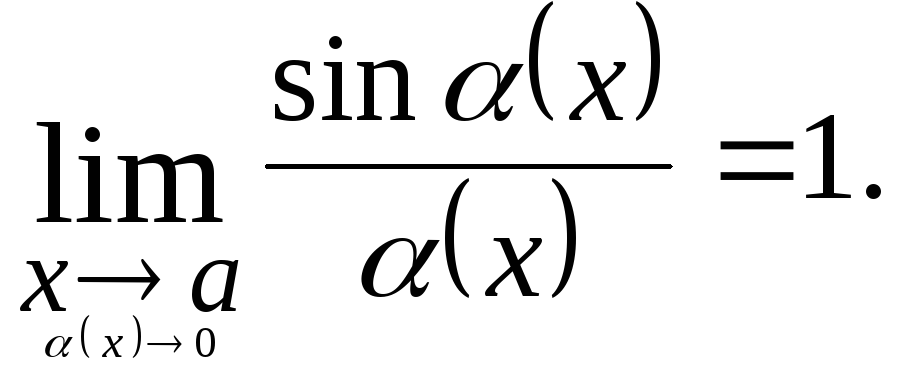
![]() ;
;
![]() ;
;
![]()
 3.
Второй замечательный предел:
3.
Второй замечательный предел:
![]()
![]()
![]()
![]()
4. Эквивалентные бесконечно малые:

Производная
1. Основные правила дифференцирования

2. Таблица производных сложных функций:



3![]()
 .
Дифференцирование функций, заданных
параметрически:
.
Дифференцирование функций, заданных
параметрически:
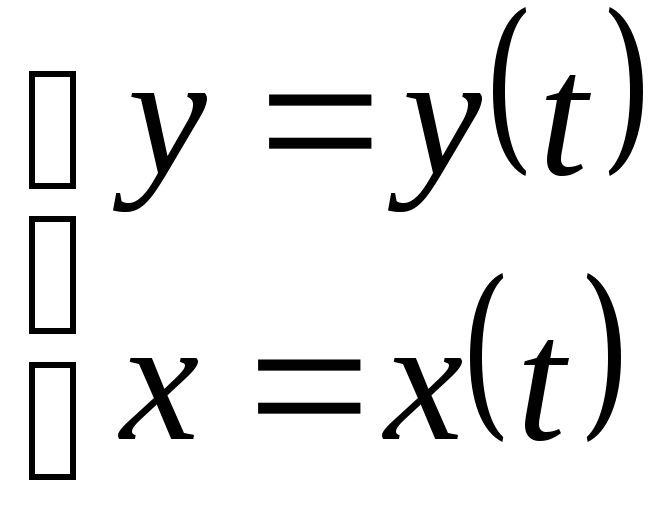
4.
Дифференциал функции
![]()
![]()
5 .
Правило
Лопиталя:
.
Правило
Лопиталя:
Функции нескольких переменных
1![]() .
Полный
дифференциал:
.
Полный
дифференциал:
2.
Производная по направлению
![]() :
:
![]()
 где
где
![]() .
.
![]()
3. Градиент: .
4![]()
![]() .
Экстремум функции двух переменных
.
Экстремум функции двух переменных
а) необходимое условие существования экстремума:
![]() б)
достаточное
условие существования экстремума:
б)
достаточное
условие существования экстремума:
![]()
![]()
![]()
![]() Если
, то
в точке экстремум
существует:
Если
, то
в точке экстремум
существует:
![]()
![]() при
- min;
при
- min;
![]() при -max;
при -max;
![]() если
, то
в точке экстремум не существует;
если
, то
в точке экстремум не существует;
если , то необходимы дополнительные исследования.
5. Приближенные вычисления:
![]()
Неопределенный интеграл
1. Основные свойства неопределенного интеграла:
![]()
![]()
2. Интегрирование по частям
В
 иды
интегралов, которые берутся по частям
иды
интегралов, которые берутся по частям
![]()
3 .Таблица
основных интегралов
.Таблица
основных интегралов



4
 .
Простейшие рациональные дроби
.
Простейшие рациональные дроби
Определённый интеграл
![]()
1. Формула Ньютона-Лейбница: ,
где
![]()
2. Свойства определённого интеграла:
![]()
![]()
![]() а)
г)
а)
г)
б)
д) если
![]() ,
то
,
то
![]()
![]()
в)
e) если
![]() ,
то
,
то
![]()
![]()
г)
![]()
3. Интегрирование по частям: .
4. Геометрические приложения определенного интеграла:
![]()
а) площадь криволинейной трапеции:
![]()
б) площадь фигуры:
![]() в)
объем тела,
образованного вращением трапеции вокруг
оси OX:
в)
объем тела,
образованного вращением трапеции вокруг
оси OX:
г) объем тела, образованного вращением трапеции вокруг оси OY:
![]()
Несобственные интегралы
1![]() .
Если
.
Если
![]() непрерывна,
то
непрерывна,
то
![]() а) ;
а) ;
![]() в)
в)
б) ;
![]()
2.
Если
![]() разрывна
при
разрывна
при
![]() ,
то
,
то
![]()
3.
Если
![]() разрывна
при
разрывна
при
![]() ,
то
,
то
![]()
4.
Если
![]() разрывна
в точке
разрывна
в точке
![]() ,
то
,
то
Дифференциальные уравнения
а) Дифференциальные уравнения первого порядка
1![]() .Уравнения
с разделяющимися переменными:
.Уравнения
с разделяющимися переменными:
2 .Однородные
дифференциальные уравнения первого
порядка:
.Однородные
дифференциальные уравнения первого
порядка:
3.Линейные дифференциальные уравнения первого порядка:
![]()
4![]() .
Уравнение Бернулли:
.
Уравнение Бернулли:
б) Дифференциальные уравнения второго порядка
5![]() .Простейшие
уравнения второго порядка допускающие
понижение порядка:
.Простейшие
уравнения второго порядка допускающие
понижение порядка:

 а)
в)
а)
в)
б)
6. Линейные однородные диф.уравнения второго порядка с постоянными
коэффициентами
|
Диф. уравнение |
|
||
|
Характер. уравнение |
|
||
|
Корни характер. уравнения |
|
|
|
|
Вид решения |
|
|
|
7. Линейные неоднородные дифференциальные уравнения второго порядка с
![]() постоянным
с коэффициентами:
постоянным
с коэффициентами:
![]()



Ряды
1![]()
![]() .
Необходимый признак сходимости ряда:
.
Необходимый признак сходимости ряда:
Если ряд сходится, то
![]()
![]()
Если , то ряд расходится.
2.Достаточные признаки сходимости знакоположительных рядов:
![]()
![]()
![]()
а) предельный признак сравнения: если и конечен, то ряды и
![]()
![]() сходятся или
расходятся одновременно;
сходятся или
расходятся одновременно;
б) признак Даламбера: если существует конечный предел то при ряд
![]()
![]()
![]() сходится,
а при - расходится;
сходится,
а при - расходится;
в![]() )
признак
Коши: если
существует предел ,
то при
ряд сходится, а
при
)
признак
Коши: если
существует предел ,
то при
ряд сходится, а
при
![]()
![]()
![]() - расходится;
- расходится;
с![]() )
интегральный
признак:
если сходится
или расходится
интеграл , где
то
ряд будет
также сходится или расходится.
)
интегральный
признак:
если сходится
или расходится
интеграл , где
то
ряд будет
также сходится или расходится.
3![]()
![]() .
Сходимость знакочередующихся рядов:
.
Сходимость знакочередующихся рядов:
![]() а) признак
Лейбница: ряд
сходится,
если: 1)
;
а) признак
Лейбница: ряд
сходится,
если: 1)
;
2) ;
![]() б) абсолютная
сходимость: если
ряд сходится и сходится
ряд
б) абсолютная
сходимость: если
ряд сходится и сходится
ряд![]() ,
то
,
то
знакочередующийся ряд сходится абсолютно;
![]() в) условная
сходимость: если
ряд сходится
и расходится ряд
в) условная
сходимость: если
ряд сходится
и расходится ряд
![]() ,
то
,
то
знакочередующийся ряд сходится условно.
4.
Радиус
сходимости степенного ряда:
![]() .
.
5. Интервал сходимости
а)
![]() для ряда
для ряда
![]() ;
;
б)
![]() для ряда
для ряда
![]()
