1.9. Основные виды записи задач линейного программирования
Определение: Общей задачей линейного программирования называют задачу:
при ограничениях
(
);
(
);
(
);
(
);
-
произвольные (
),
где
,
,
- заданные действительные числа.
Определение: Симметричной формой записи задачи линейного программирования называют задачу:
при ограничениях
(
);
(
);
или задачу
при ограничениях
(
);
(
).
Определение: Канонической формой записи задачи линейного программирования называют задачу:
при ограничениях
(
);
(
).
Рассмотрим еще два вида записи- матричную и векторную.
Введем
обозначения:
,
,
,
,
где
С – матрица-строка; А – матрица системы
уравнений, Х – матрица-столбец переменных,
- матрица-столбец свободных членов.
Каноническая форма записи примет вид:
или
max Z=CX
при ограничениях
,
или
,
.
Запишем задачу линейного программирования в векторной форме:
,
,
...,
,
...,
.
Тогда задача линейного программирования в канонической форме записи имеет вид:
при ограничениях
,
,
где
- скалярное произведение векторов
и
.
1.10. Способы преобразования
При
необходимости задачу минимизации можно
заменить задачей максимизации и наоборот.
Для функции одной переменной это
утверждение очевидно. В самом деле, если
- точка максимума функцииy=f(x),
то для функции y=-f(x)
она является точкой максимума, так как
графики функций f(x)
и –f(x)
симметричны относительно оси абсцисс
(рис. 1).
Итак,
min f(
)
= max (-f(
)).
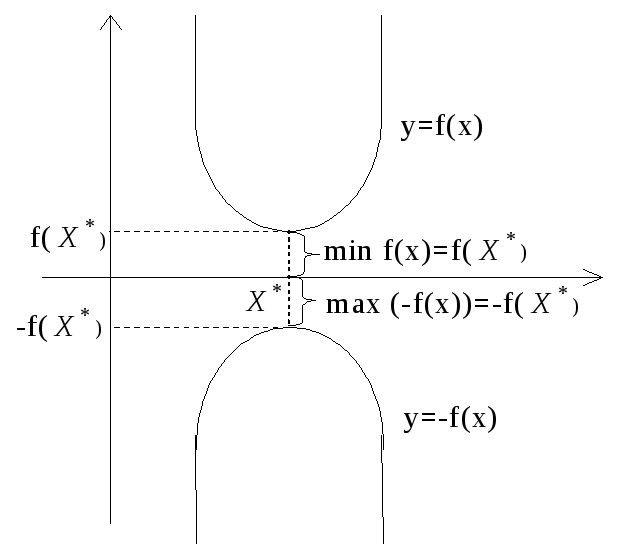
Рис. 1. Графики функций y=f(x) и y=-f(x).
То же самое имеет место в случае функции n переменных:
.
1.11. Переход к канонической форме
Из примеров задач линейного программирования следует, что большинство ограничений задается неравенствами. Основные же методы решения задач линейного программирования применяются лишь к задачам, записанным в канонической форме. Поэтому приходится переходить от любой формы записи задач линейного программирования к ее каноническому виду, причем, нужно быть уверенным, что эти формы эквивалентны.
Пусть исходная задача линейного программирования имеет вид:
при ограничениях:
(
); (1)
(
); (2)
(
).
Преобразуем
ее к каноническому виду. Введем m
дополнительных неотрицательных
переменных
(
).
Для того чтобы неравенства типа
преобразовать в равенства, к их левым
частям прибавим дополнительные переменные
(
)
после чего система неравенств (1) примет
вид:
(
) (3).
Для
того чтобы неравенства типа
(2) преобразовать в равенства, из их левых
частей вычтем дополнительные переменные
(
).
Получим:
(
) (4).
Систему уравнений (3) и (4) с условием неотрицательности дополнительных переменных называют эквивалентной системе неравенств (1) и (2) соответственно.
Дополнительные
переменные
(
)
в целевую функцию вводятся с коэффициентами,
равными 0.
Получим задачу:
,
при ограничениях:
(
);
(
);
(
);
(
).
Теорема
11.1 (о переходе к канонической форме
записи) Каждому допустимому решению
задачи
Соответствует
вполне определенное допустимое решение
задачи
И
наоборот, каждому решению
задачи (6) соответствует допустимое
решение
задачи (5).
Пример 1. Привести к канонической форме записи задачу:
Найти:
при ограничениях:
,
,
.
Решение.
при ограничениях
,
,
,
,
,
.
Пример 2. Привести к канонической форме записи задачу:
Найти:
при ограничениях:
,
,
.
Решение.
при ограничениях
,
,
,
,
,
.
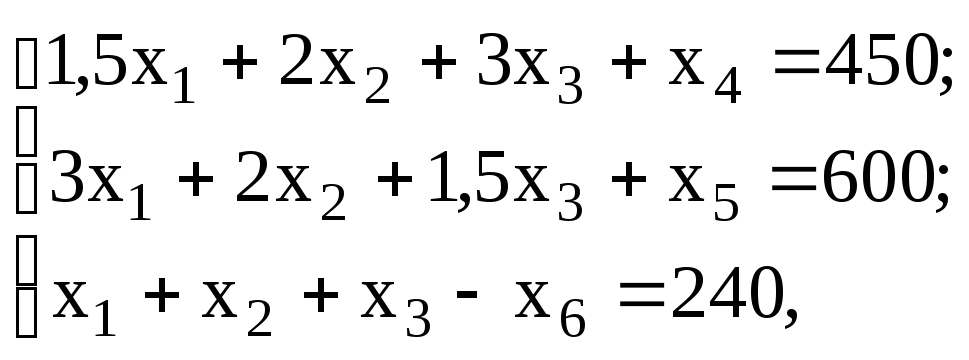
Отметим экономический смысл дополнительных переменных. Они в каждой задаче прямо связаны с ее экономическим содержанием. Например, для задачи о наилучшем использовании ресурсов:
(
),
т.е. дополнительная переменная указывает величину неиспользованного ресурса. Для задачи о смесях:
(
),
т.е. дополнительная переменная показывает потребление соответственного питательного вещества в оптимальном плане сверх нормы.
В
ряде производственно-экономических
ситуаций не на все переменные налагаются
условия неотрицательности. В подобных
ситуациях, даже если ограничения
представлены в виде равенств, задача
не будет канонической. Для представления
такой задачи в каноническом виде каждую
из переменных
,
на которые не наложено условие
неотрицательности, заменим разностью
двух неотрицательных переменных
и
,
т.е.
,
где
0 и
0 (этим приемом мы воспользуемся при
изучении двойственных задач).