Работа и энергия.

1. Работа силы.

Работа , выполняемая силойпри малом перемещениитела, определяется следующим образом

, (52)

или

,

- угол между направлениями силы и перемещения. Если сила перпендикулярна перемещению, т.е., то работа силой не совершается, т.к..

Полная работа на пути

. (53)

Если тело движется прямолинейно и действующая на тело сила постоянна, то естьине меняются, то работа силы на путиравна

. (54)

Единица измерения работы Дж (Джоуль).

• Работу силы тяжести 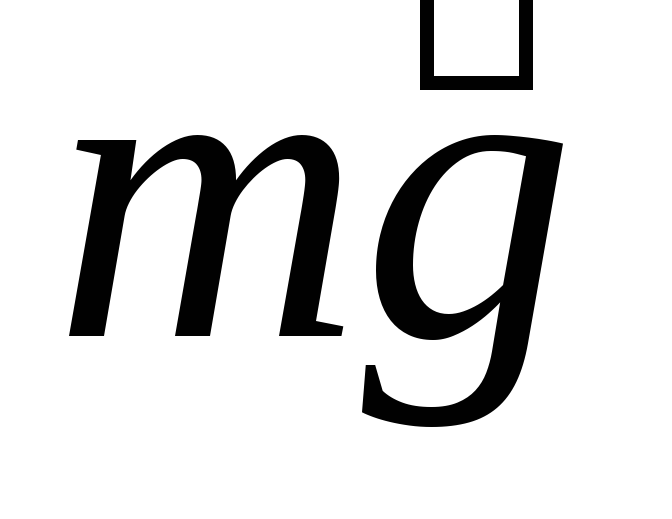можно подсчитать по упрощенной формуле

, (55)

- величина перемещения тела вдоль действия силы тяжести, «» выбирается при движении тела вниз, «-» - при движении тела вверх.

• Работа силы упругости равна

, (56)

- коэффициент упругости пружины, и- ее начальная и конечная деформации.

Силы, работа которых не зависит от траектории движения тела, а определяется его начальным и конечным положением, называютсяконсервативными. В механике к таким силам относятся сила тяжести и сила упругости .

Мощность представляет собой работу, произведенную в единицу времени, т.е.

, (57)

где - работа, совершенная за время. Единицей измерения мощности являетсяВатт (Вт).

2. Работа момента силы.

При вращении, когда тело поворачивается на малый угол , моментсилы совершает работу

. (58)

При повороте на угол работа равна

.

Если момент силы не зависит от угла поворота, то

. (59)

3. Механическая энергия.

Энергия является мерой способности тел совершать работу. Механическая энергия складывается из кинетической и потенциальной. Первая обусловлена движением тела, вторая - видом сил, действующих на тело и положением тела в пространстве.

Для материальной точки и поступательно движущегося тела кинетическая энергия равна

, (60)

для вращающегося тела она представляет собой сумму кинетических энергий отдельных точек тела

.

В итоге, для вращающегося тела,

. (61)

- момент инерции тела относительно оси вращения, - его угловая скорость.

Потенциальной энергией обладают тела, находящиеся под действием консервативных сил. Если тело перемещается консервативными силами из точки 1 в точку 2, то изменение потенциальной энергии тела определяется как работа этих сил

. (62)

Из (62) можно найти только изменение потенциальной энергии, ее величина может быть определена лишь с точностью до постоянного слагаемого. Поэтому начало отсчета потенциальной энергии может быть выбрано произвольно.

Консервативная сила по величине равна скорости изменения потенциальной энергии в направлениидействия силы,

. (63)

Знак минус в уравнении (63) отражает тот факт, что консервативная сила всегда направлена в сторону убыли потенциальной энергии.

Если тело находится под действием силы тяжести, его потенциальная энергия

, (64)

- высота расположения тела над уровнем отсчета.

Если на тело действует сила упругости, его потенциальная энергия

, (65)

- величина деформации пружины.

4. Теорема о кинетической энергии. Закон сохранения механической энергии.

Существует теорема о кинетической энергии: изменение кинетической энергии системы тел равно сумме работ всех сил, приложенных к этой системе

. (66)

Работу всех сил можно разделить на работу сил консервативных и неконсервативных

.

Сумма работ консервативных сил равна изменению потенциальной энергии системы

.

Тогда уравнение (66) можно переписать в виде

.

Т.е. изменение механической энергии системы равно работе неконсервативных сил

. (67)

Из (67) следует закон сохранения механической энергии: механическая энергия системы тел сохраняется, если работа неконсервативных сил, действующих на систему, равна нулю. Работа консервативных сил при движении тел не ведет к превращению механической энергии в другие ее виды.