Тема 6. Ряды динамики

Ряд динамики- это ряд значений статистического показателя, характеризующих изменения явления во времени.

Уровни ряда могут быть выражены абсолютными, относительными или средними величинами. Динамические ряды могут быть интервальными и моментными. Изучение динамических рядов предполагает определение среднего уровня ряда динамики, определение показателей динамики и их усреднение, анализ закономерностей изменения уровней ряда.

Метод определения среднего уровня зависит от типа динамического ряда. Средний уровень интервального ряда определяется как средняя арифметическая простая, где n- число уровней ряда.

Средний уровень моментного ряда определяется:

а) для ряда с разноотстоящими моментами наблюдения по формулам:

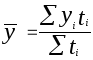1. или 2.,.

б) для ряда с равноотстоящими моментами наблюдения по средней хронологической:

Изменение динамического ряда характеризуют с помощью показателей динамики. К ним относятся: абсолютный прирост, коэффициент (темп) роста, процент (темп) прироста, абсолютное значение одного процента прироста. В зависимости от базы сравнения различают базисные и цепные показатели динамики. Базисные показатели динамики- это результат сравнения текущих уровней с одним фиксированными уровнем, принятым за базу (обычно начальным). Цепные показатели динамики- это результат сравнения текущих уровней с предшествующими. Формулы расчета представлены ниже:

1. Абсолютный прирост

Базисный	цепной

2. Коэффициент роста

Базисный	цепной

Темп роста

3. Процент прироста

базисный	цепной

Абсолютное значение одного процента прироста

.

4) Средние показатели динамики определяются следующим образом:

Средний абсолютный прирост

;

Средний темп роста

;

;

Средний темп прироста .

Для выявления закономерностей (тенденции) динамического ряда производят сравнение эмпирического ряда с рядом теоретическим, построенным с помощью подбора функции (метод аналитического выравнивания). При аналитическом выравнивании статистические приемы сводятся к тому, что нужно подобрать математическую функцию, значения которой наиболее близки к уровням выравниваемого ряда. В качестве независимой переменной выступает фактор времени ( t).

Выравнивание ряда сводится к определению параметров функции (уравнений).

Система уравнений:

1. Линейное уравнение

2. Уравнение параболы 2-го порядка

3. Уравнение гиперболы

4. Уравнение степенной функции

5. Уравнение логарифмическое

6. Уравнение показательной функции и др.

Адекватная функция используется в последствии для прогнозирования ряда.

Метод экстраполяциирезультатов:

1. МЕТОД СРЕДНЕГО АБСОЛЮТНОГО ПРИРОСТА

При экстраполяции уровней развития изучаемого явления на базе ряда динамики с постоянными абсолютными приростами применяется формула: , где- экстраполируемый уровень;

- уровень исследуемого объекта в последнюю точку предистории;- средний абсолютный прирост исследуемого объекта в предистории;t– срок прогноза (период упреждения).

2) МЕТОД СРЕДНЕГО ТЕМПА РОСТА

При экстраполяции уровня развития изучаемого явления на базе ряда динамики со стабильными темпами роста используют следующую формулу: , где- средний коэффициент роста.