Основные законы аэро- и гидромеханики.

Аэро- и гидромеханика изучает движение жидкостей и газов, плотность которых имеет постоянную величину.

Плотность вещества

, кг/м³ . (68)

масса вещества в объеме .

Давление

, Па (Паскаль). (69)

сила, действующая перпендикулярно площадке .

Законы гидростатики.

1. Закон Паскаля. Давление, оказываемое на жидкость, передается во все ее точки, по всем направлениям, без изменения.

2. Гидростатическое давление. Гидростатическим называется давление, обусловленное весом жидкости. Величина гидростатического давления

, (70)

плотность жидкости, - ускорение свободного падения,- высота столба жидкости. Уровни равного давления в жидкости всегда горизонтальны.

3. Закон Архимеда. На тело, погруженное в жидкость (газ), действует выталкивающая сила Архимеда

, (71)

плотность жидкости, - ускорение свободного падения,объем тела, погруженного в жидкость.

Законы гидродинамики.

1. Уравнение неразрывности струи.

При ламинарном (слоистом) течении жидкости произведение площади сечения трубки тока на скорость жидкости в этом сечении является величиной постоянной вдоль линии тока

, (72)

и - площади сечений 1 и 2 трубки тока,и- скорости частиц жидкости в этих сечениях.

2. Уравнение Бернулли.

Жидкость называется идеальной (невязкой), если можно пренебречь силами трения между ее слоями.

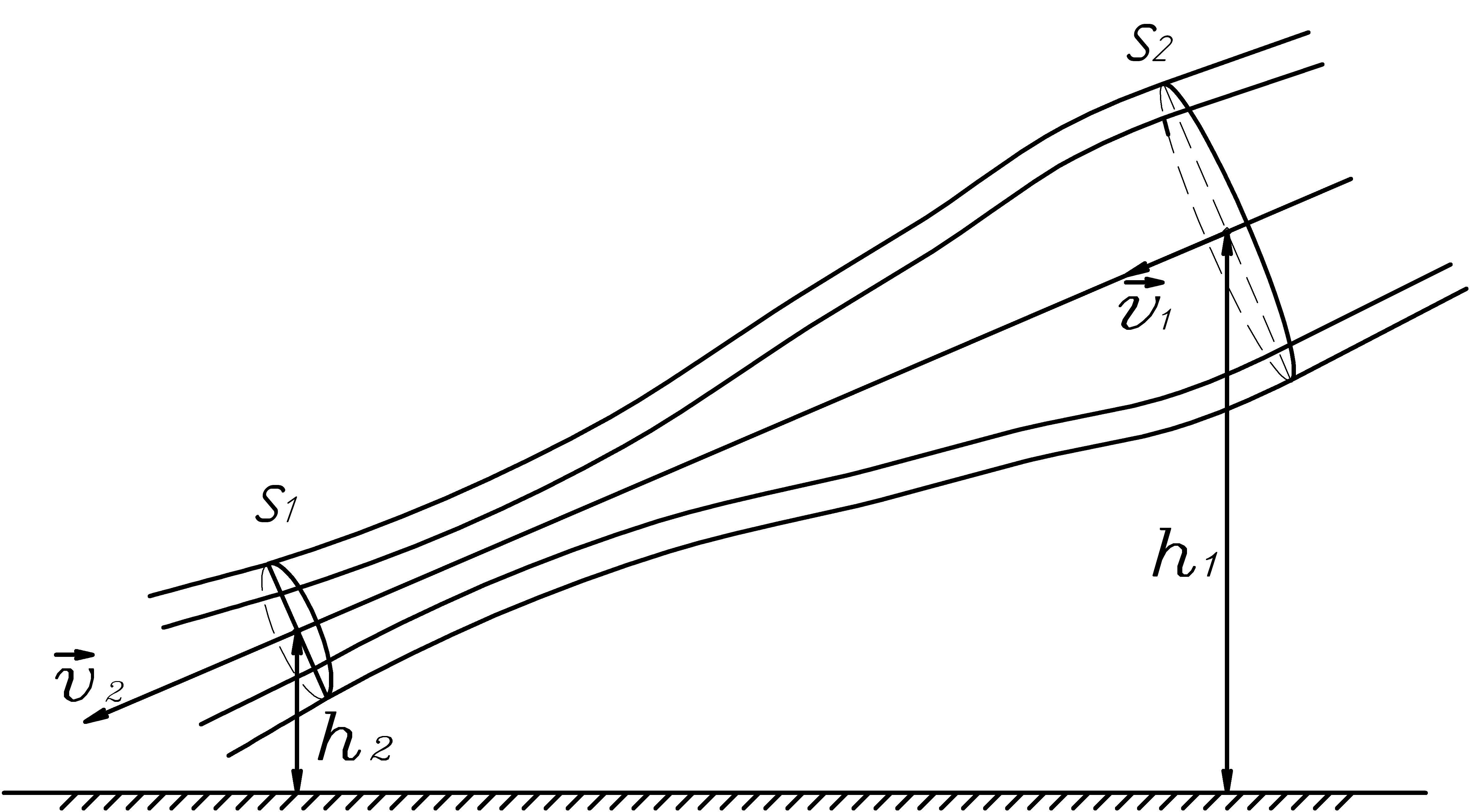
Рисунок 8- Трубка тока жидкости.

Для идеальной жидкости при ламинарном течении выполняется уравнение Бернулли

= , (73)

и - статическое давление (давление жидкости на площадку, расположенную вдоль линии тока) в сечениях 1 и 2 трубки тока (рис. 8);

и - динамическое давление в этих сечениях, обусловленное движением жидкости (кинетическая энергия единицы объема жидкости в сечениях 1 и 2);

и - высоты, на которых расположены сечения; плотность жидкости; и- потенциальная энергия единицы объема жидкости в сечениях 1 и 2.

Основы релятивистской механики.

Теория относительности (релятивистская механика) описывает движение объектов, скорость которых близка к скорости светам/с в вакууме. Она основывается на двух принципах, сформулированных А. Эйнштейном.

1-й принцип (принцип относительности): все законы природы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой, т.е. имеют одинаковую форму во всех инерциальных системах отсчета.

2-й принцип (постоянство скорости света): скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от скорости движения источника или приемника света.

Следствия теории относительности:

1. Релятивистский закон сложения скоростей.

Рассмотрим систему отсчета , относительно которой системадвижется со скоростью, проекция которой на осьравна(рис. 9). Тело движется в системесо скоростью. Тогда скорость этого же тела в системеравна

,

в отличие от классического соотношения .

Рисунок 9 – Неподвижная и подвижная системы отчета.

2. Одновременность событий в разных системах отсчета.

Два события, происходящие в различных точках пространства и одновременные с точки зрения наблюдателя, находящегося в одной системе отсчета, не являются одновременными для наблюдателя в другой системе отсчета.

3. Замедление времени.

Пусть - длительность события в точке, неподвижной относительно системы отсчетаx,y (время называют « собственным временем»). Обозначим черездлительность этого же события в системеx’y’, относительно которой система x,y движется со скоростью . Интервалы времениисвязаны соотношением

, (74)

где . Всегда параметри, т.е. длительность события, происходящего в определенной точке, является наименьшей в системе отсчета, относительно которой эта точка неподвижна.

4. Сокращение длины.

Обозначим через длину тела в системе отсчета, относительно которой тело покоится, а через- длину в системе, относительно которой оно движется со скоростью. Тогда

. (75)

<, т.е. длина тела наибольшая в системе отсчета, относительно которой тело неподвижно. Сокращение длины происходит только в направлении движения тела, поперечные движению размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.

5. Зависимость массы 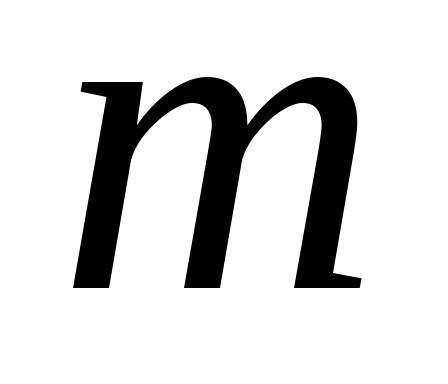тела от скорости его движения.

, (76)

-масса покоя тела, т.е. масса в системе отсчета, относительно которой тело покоится.

6. Импульс частицы.

Импульс релятивистской частицы

.

Основной закон релятивистской динамики материальной точки

),

- результирующая всех сил, приложенных к этой точке.

7. Взаимосвязь массы и энергии.

Энергия тела (без учета потенциальной энергии во внешнем силовом поле) связана с его массой

, (77)

- скорость света в вакууме.

Энергия покоя тела

,

- масса покоящегося тела.

Кинетическая энергия релятивистской частицы

.

8. Связь между энергией и импульсомчастицы.

. (78)

Образец теста по разделу «Механика»

1. Материальная точка движется по окружности радиусом = 5 м так, что пройденный ею путь меняется со временем как м. Определить величину ускорения точки в момент = 2 с. В произвольной точке траектории показать направления тангенциального, нормального и полного ускорения материальной точки.

(Ответ: ≈ 20 м/с² )

2. Диск вращается равнозамедленно в направлении, показанном на рисунке. Определить номер линии, по которой направлен вектор углового ускорения .

(Ответ: 1)

3. В каком случае скорость тела можно вычислить по формуле? Указать номер правильного ответа.

1: =6м2: =6м 3: =(6+) м4: =(6+1) м

(Ответ: 1)

4. Тело массой = 2 кг падает вертикально вниз с ускорением=9 м/с² . Определить среднюю силу сопротивления воздуха.

(Ответ: 2 Н)

5. Четыре шарика массами , 2, 3, 4закреплены на невесомом стержне на одинаковом расстоянии= 0,1 м друг от друга. На каком расстоянии от крайнего левого шарика находится центр масс системы?

(Ответ: 20 см)

6. Четыре шарика одинаковой массы = 50 г закреплены невесомыми стержнями в вершинах квадрата со стороной= 10 см. Определить момент инерциисистемы относительно оси. Шарики рассматривать как материальные точки.

(Ответ: 0,001 кг· м²)

7. Чтобы закатить барабан радиуса = 1 м на ступеньку высотой= 50 см, к нему прикладывают горизонтальную силу= 2 Н. Определить величину моментаэтой силы относительно точки О.

(Ответ: 3 Н· м)

8. С какой угловой скоростью должен вращаться диск радиуса= 0,8 м и массой= 0,5 кг, чтобы его кинетическая энергия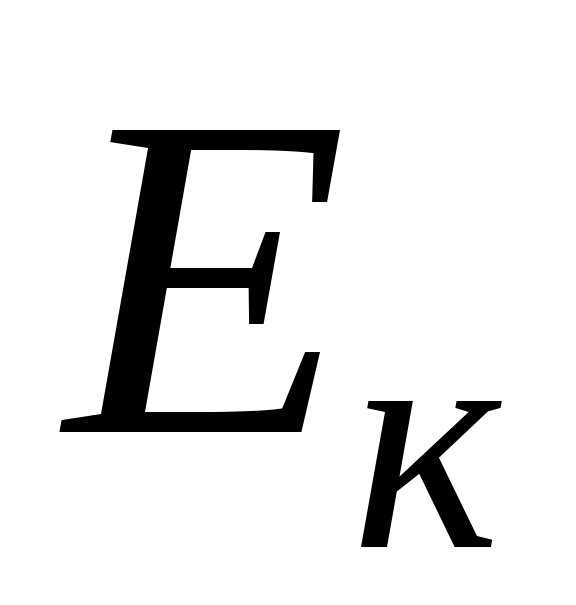составляла 2 Дж?

(Ответ: 5 рад/c)

9. Стержень длиной 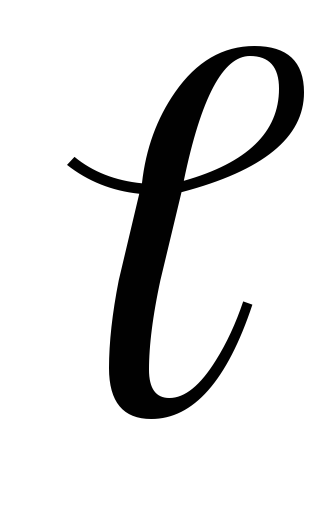= 1 м ставят вертикально на конеци отпускают. Стержень падает без проскальзывания, вращаясь вокруг точки. Определить угловое ускорениестержня в момент, когда он составляет угол= 60° с плоскостью.0,9;=0,5.

(Ответ: 7,5 рад/с²)