fizick_praktika_II

где Q – электрический заряд на пластине конденсатора; U – разность потенциалов между пластинами конденсатора.

Электроемкость плоского конденсатора равна

где S – площадь одной пластины; d – расстояние между пластинами. Если в конденсатор поместить диэлектрик, то для создания разности потенциалов в 1 В потребуется больший заряд. Это означает, что емкость конденсатора с диэлектриком увели-

чивается в раз:

Таким образом, емкость конденсатора прямо пропорцио-

нальна диэлектрической проницаемости среды, заполняющей пространство между обкладками.

Конденсаторы используются в электрических цепях как устройства, способные поглощать или выделять большие количества заряда. Рассмотрим подробнее закономерности изменения тока в цепи при зарядке и разрядке конденсатора и возможность их использования для определения диэлектрической про-

ницаемости конденсатора.

3.5.Процессы установления тока при разрядке

изарядке конденсатора

Разрядка конденсатора. Рассмотрим зависимость силы тока от времени при разрядке и зарядке конденсатора, если в цепи с конденсатором имеется сопротивление (рис. 3.3). Решение этой задачи получают в предположении, что мгновенное значение тока одно и то же во всех поперечных сечениях проводника, соединяющего обкладки конденсатора, а мгновенное электрическое поле такое же, как и электростатическое поле на обкладках конденсатора при тех же зарядах. Токи

41

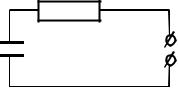
Rи поля, удовлетворяющие этим условиям, называются квазистационарными.

между обкладками. Считая ток в проводнике положительным, когда он течет от заряженной положительно обкладки конденсатора к обкладке конденсатора, заряженной отрицательно, можем написать

где С – электроемкость конденсатора; R – сопротивление проводника; dQ – величина изменения заряда за время dt. Знак «минус» означает, что ток возникает при уменьшении заряда на обкладках конденсатора.

Исключая U и I в уравнениях (3.15), получим

После интегрирования этого уравнения придем к соотношению

где Q0 – начальное значение электрического заряда конденсатора; RC – постоянная, имеющая размерность времени и на-

зываемая временем релаксации. Через время заряд конденсатора убывает в e раз. Таким образом, разряд конденсатора через сопротивление R происходит тем быстрее, чем меньше емкость C и сопротивление цепи.

42

Дифференцируя соотношение (3.17) по времени t, находим закон изменения тока во времени:

где I0 = Q0/ – значение тока в начальный момент времени t = 0. Поскольку напряжение на сопротивлении изменяется в одной фазе с силой тока, то, используя закон Ома, получим

закон изменения напряжения на резисторе:

где U0 – ЭДС источника тока.

Зарядка конденсатора. Задача о зарядке конденсатора решается аналогично. При зарядке конденсатора заряд на обкладках конденсатора изменяется согласно закону:

где Q = CU0; RC – время релаксации. Видно, что зарядка конденсатора C через сопротивление R происходит тем быстрее, чем меньше сопротивление цепи и емкость конден-

В настоящей работе необходимо определить диэлектри-

ческую проницаемость конденсатора при использовании последнего для получения определенных изменений в напряжении U в результате изменения заряда на обкладках конденсатора. Для достижения данной цели используем закон изменения напряжения на обкладках конденсатора в процессе его разрядки, при этом источником напряжения в цепи будет

43

служить генератор импульсных/синусоидальных колебаний напряжения.

Лабораторная работа включает две части. В первой части работы используется генератор импульсных колебаний, а во второй части – генератор синусоидальных колебаний.

4.ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

4.1.Описание установки

Работа выполняется на установке, подключенной к компьютеру с помощью соединительного кабеля (рис. 3.4). Установка представляет собой электрическую цепь (рис. 3.5). С помощью компьютера осуществляется запуск и работа двухканального осциллографа и генератора импульсных (синусоидальных) колебаний.

44

лучевая трубка. Нагретый катод эмитирует электроны, которые движутся в электростатическом поле с ускорением к аноду. Таким образом, создается электронный пучок. Движение электронного пучка в электронно-лучевой трубке управляется отклоняющими пластинами, между которыми создается разность потенциалов. Горизонтальные пластины обеспечивают движение электронного пучка вверх и вниз на экране, а вертикальные пластины – вправо и влево. На горизонтальные пластины подается напряжение, пропорциональное напряжению в цепи, а на вертикальные пластины – напряжения, пропорциональные времени, в течение которого изменяется напряжение в цепи. Таким образом, на экране осциллографа создается временная развертка переменного напряжения в цепи.

C

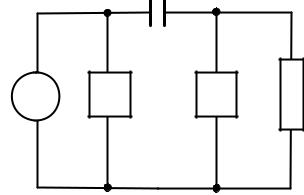
Рис. 3.5. Электрическая цепь, содержащая конденсатор C, резистор R и источник импульсных (синусоидальных) колебаний G

4.3. Описание схемы установки

Электрическая цепь (рис. 3.5) состоит из генератора переменного тока G (импульсных и синусоидальных колебаний напряжения), конденсатора С, активного сопротивления R идвух-

45

канального осциллографа (каналы N1 и N2). Первый канал осциллографа N1 позволяет получить зависимость напряжения от времени на генераторе (G), а второй канал N2 – на сопротивлении R в цепи после конденсатора С.

Вариант 1

5.ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПОСТОЯННОЙ СРЕДЫ МЕТОДОМ РЕЛАКСАЦИИ НАПРЯЖЕНИЯ

5.1.Описание метода измерения

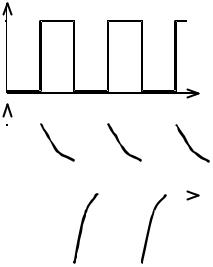
Генератор импульсных колебаний подает в цепь прямоугольные импульсы напряжения. Закон изменения напряжения имеет вид, изображённый на рис. 3.6, а. На сопротивлении R вид электрического импульса напряжения изменяется по сравнению с импульсом напряжения на генераторе (рис. 3.6, б).

46

Для девяти точек на кривой 1 определяют напряжение U и соответствующее время t, а затем строят график зависимости

ln UU0 f (t) . По оси абсцисс откладывают время t, а по оси ор-

динат – величину ln UU0 . Затем находят время релаксации из графика. Для этого определяют из графика для двух момен-

Если между обкладками конденсатора находится диэлектрик с диэлектрической проницаемостью , то наклон прямой на

графике ln UU0 f (t) изменится. Строят график зависимости

ln UU0 f (t) во втором случае и определяют время релаксации 2.

Таким образом, можно записать, что 1 RC1 , 2 RC2 и активное сопротивление равно:

47

Из соотношения (3.26) получаем

Используя соотношения (3.13), (3.14) и (3.27), находим, что диэлектрическая проницаемость среды в конденсаторе равна:

где 1 – время релаксации для цепи с конденсатором, в котором диэлектриком является воздух ( 1), и 2 – время релаксации

вцепи с конденсатором с диэлектриком ( > 1).

5.2.Порядок выполнения работы

1.Подключите установку к контроллеру с помощью соединительного кабеля.

2.Подключите установку к электрической сети 220 В.

3.На установке нажмите кнопку «Сеть».

4.Включите компьютер и запустите Windows.

5.Откройте папку с лабораторной работой «Определение диэлектрической проницаемости диэлектрика».

6.Запустите файл Start. bat. На экране появится совмещенное окно двухканального осциллографа и импульсного генератора (рис. 3.7).

7.Для запуска работы включите питание импульсного генератора и осциллографа, нажав мышкой соответствующие кнопки «Вкл.». Питание синусоидального генератора при этом должно быть выключено.

8.Настройте генератор импульсов на заданную частоту и длительность. Для этого вращением рукоятки «Период» выставляют величину периода колебаний 1500 мкс, а вращением

48

рукоятки «Длительность», устанавливают величину длительности импульсов 500 мкс.

9. Проведите настройку каналов N1 и N2 осциллографа. Напомним, что канал N1 дает форму импульсов генератора (на экране ему соответствует зеленая линия), а канал N2 дает форму импульсов на резисторе в RC-цепочке (на экране ему соответствует линия красного цвета). Для настройки канала N1:

а) регулятором «Усиление Х» установите масштаб 0,15 мс/деление шкалы, а регулятором «Усиление Y» установить 1,5 В/дел;

б) установите синхронизацию, для чего подведите курсор к окошку на панели и выберите тип генератора (для импульсного генератора – импл. ген.), щелкните левой кнопкой мышки;

в) регуляторы «Смещение Х» и «Смещение Y» установите в среднее положение (стрелки расположены вертикально вверх) так, чтобы изображение импульса было расположено в центре экрана и горизонтальная линия сигнала соответствовала нулевому положению;

г) подобным образом настройте канал осциллографа N2.

10. Определите время релаксации 1 для случая, когда между конденсаторами находится воздух. Для этого следует снять показания напряжения и времени с фронта импульса (кривая 1) и занести их в таблицу. Для снятия показаний используют две подвижные горизонтальные линии и две подвижные вертикальные линии (рис. 3.7), которые можно передвигать мышкой. Нижнюю горизонталь с помощью мышки надо установить в нулевое положение на экране, а верхнюю горизонталь установить

внекоторую точку пересечения с кривой 1, соответствующей фронту импульса. Левую вертикаль отвести в точку начала спада напряжения, а правую вертикаль подвести к горизонтали

вточке пересечения с кривой фронта импульса. Далее, используя левую кнопку мышки, нажать кнопку «Съем данных». В таблице результатов на экране при этом появятся измеренные значения U и t. Перемещая перекрестие горизонтали и вертика-

49

ли, подобным образом производят измерения для других точек кривой 1 фронта импульса (9 точек).

Рис. 3.7. Изображение двухканального осциллографа и генератора импульсных/синусоидальных колебаний

11.Описанным выше способом измерьте U0 (напряжения начала спада кривой 1).

12.Данные в таблице на экране перенесите в табл. 3.1: Используя данные табл. 3.1, постройте график зависимости

ln UU0 f (t) .

Таблица 3.1

Данные напряжения и времени для определения времени релаксации 1

50